Глава 2 фотоны (Корпускулярные свойства волн)

Волновая природа вещества качествен­но проявляется в том, что каждой частице присущи свойства волны и, наоборот, любые волны имеют свойства, харак­терные для частиц. В качестве первого при­мера, демонстрирующего это свойство волн, мы приведем фотоэффект, теорию которого Эйнштейн разработал в 1905 г.

§1 Фотоны и их свойства

Эйнштейн выдвинул гипотезу, что носителем дискретного кванта энергии света является своеобразная частица, которая получила название фотона. Следовательно энергия не только излучаются и поглощается квантами, но и между этими процессами проявляется в виде частицы, которая возникает при излучении света и погибает при его поглощении. Между этими процессами превращения, фотон движется со скоростью, всегда равной скорости света в вакууме () и уничтожение фотона может рассматриваться как элементарный акт передачи его энергии какому-либо другому обьекту.

Фотон должен иметь вполне определённую массу, которая в соответствии с основными положениями специальной теории относительности может быть определена из следующего соотношения:

поэтому фотон не может обладать массой покоя

конечная масса получается только для . Итак, фотон всегда находится в движении и не обладает массой покоя. Этим он отличается от элекрона, протона и некоторых других частиц.

Для частиц с нулевой массой

; фотон летит в направлении распространения

э/м волны.

§ 2. Фотоэффект

В конце XIX столетия был открыт элек­трон. Вскоре после этого обнаружили, что электроны вылетают с некоторых металли­ческих поверхностей, когда на эти поверхности падает свет достаточно высокой частоты (для всех металлов, кроме щелочных, необходим ультрафиолетовый свет). Это явление известно под названием фотоэлектрического эффекта (рис.2). 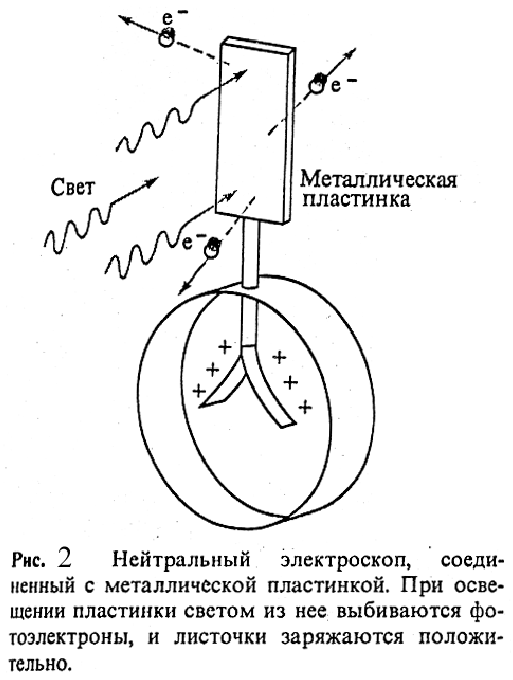Со времени дифракционных экспериментов Юнга на двух щелях не было сомнений в том, что свет представляет собой волны. Эти пред­ставления позволяли объяснить фотоэф­фект. Амплитуда колебаний свободного электрона в переменном электрическом по­ле записывается в виде: .

Поэтому можно было ожидать, что элек­трон, расположенный вблизи поверхности, покинет металл, как только амплитуда его колебаний А превысит некоторое критиче­ское значение. Из волновой теории света мы имеем следующие выводы: 1)электроны не будут вылетать из металла, до тех пор пока не превысит определенного критического значения; 2) энергия испу­щенных электронов возрастает пропорционально и 3) если величину (а значит, и интенсивность) поддерживать постояной, а частоту света увеличивать, то число испускаемых электронов должно умень­шаться.

На рис.3 показана схема одного из приборов, который был использован в наиболее точных опытах. В трубке, из которой откачан воздух, находятся два электрода, связанные с внешней цепью; анодом служит металлическая пластинка, поверхность которой должна облучаться. Часть фотоэлектронов, испускаемых облучаемой поверхностью, обладает достаточной энергией для того, чтобы достичь катода, несмотря на его отрицательную полярность. Эти электроны создают в цепи ток, который измеряется амперметром. При повышении тормозящего потенциала V все меньше и меньше электронов может достичь катода, и ток уменьшается. В конце концов, когда V становиться равным или больше некоторого значения (порядка нескольких вольт) электроны больше не могут попасть на катод, и ток прекращается.

Что показал эксперимент по поводу рассмотренных выше пунктов 1-3? Все эти предсказания были опровергнуты:

1. Пороговой интенсивности обнаружено не было. Число вылетающих электронов oкaзaлocь cтpого прoпopциoнaльным при любой сколь угодно малой интенсивности.

2. Энергия электронов оказалась не зависящей от величины .

3. Обнаружена зависимость энергии электронов от частоты. Оказалось, что существует пороговая частота , причем при частотах, превышающих пороговую, энергия выбитых электронов линейно увеличи­вается с ростом частоты. Фактически кине­тическая энергия электронов менялась в интервале от нуля до некоторого значе­ния и не было электронов с энергией больше . На рис.4 приведена найденная из опыта зависимость от ча­стоты  падающего света.

В 1905 г. Эйнштейн (хотя ему еще не были известны все эти экспериментальные факты) дал правильное объяснение фо­тоэффекта. Ученый высказал весьма сме­лую по тем временам мысль. Он предпо­ложил, что свет представляет собой сово­купность квантов, каждый из которых, обладает энергией Е = h, где h-постоян­ная Планка. Эйнштейн также предполо­жил, что эти кванты света (теперь их назы­вают фотонами) ведут себя подобно мате­риальным частицам и что при столкнове­нии с электроном в металле фотон может поглотиться, а вся его энергия перейдет к электрону. Даже самому Планку это ка­залось крайне странным. Каким образом, подчиняясь, как известно, законам интер­ференции волн, свет мог в то же самое вре­мя состоять из частиц? Ведь тогда в опыте с двумя щелями частица света проходила бы либо через одну, либо через другую щель и, следовательно, не была бы в со­стоянии создать интерференционную кар­тину.

И все же теория Эйнштейна сумела объяснить экспериментальные факты. Предположим, что для удаления поверх­ностного электрона из металла необходи­мо затратить энергию W₀. Тогда, поглотив фотон с энергией h и вылетев с поверхно­сти, электрон будет иметь энергию h-W₀. Это и есть максимально возможная кинетическая энергия:

K_max=h-W₀ (фотоэффект). (1)

Данное соотношение согласуется с экспе­риментальной прямой, изображенной на рис. 4 Эйнштейн предсказал, что наклон прямой должен быть равен постоянной Планка h. Его теория фотоэффекта выдер­жала это трудное испытание. Наклон дей­ствительно оказался равен

h = 6,6310^-34 Джс (постоянная Планка)

(единицей измерения постоянной Планка является джоуль-секунда или кгм² с^-1).

Величина W₀ называется работой выхо­да и зависит от свойств данного металла. Свободный электрон вне металла испыты­вает вблизи его поверхности притяжение. Если электрон сначала покоился, то, про­никнув в металл, он приобретет кинетиче­скую энергию U₀. Иными словами, мы утверждаем, что систему электрон и ме­талл можно представить в виде потен­циальной ямы глубиной U_o, как схемати­чески показано на рис. 5. Внутри металла внешние атомные электроны оказываются сво­бодными (т.е. они не связаны с опреде­ленными атомами) и их кинетическая энер­гия может меняться от нуля до К_f. Величина К_f называется энергией Ферми. Если электрону с энергией Ферми сооб­щить дополнительно энергию W₀, то его энергии К= К_f +W₀ едва хватит на то, чтобы покинуть металл. Иными словами, когда он вылетит из металла, энергия элек­трона станет равной К=0. Из рис. 5а) видно, что W₀+ К_f =U₀ или

W₀=U- К_f (2)

Схематическая иллюстрация фотоэффекта представлена на рис. 5б). Первоначально электрон находится на уровне с энергией К_f (этот уровень показан на рисунке штри­ховой линией). После поглощения фотона с энергией h электрон переходит на более высокий энергетический уровень, обозна­ченный на рисунке сплошной верхней ли­нией. При этом энергия электрона вне ме­талла оказывается равной h-W₀. Это и есть максимально возможная энергия, которую может иметь испущенный элек­трон: К_макс=h-w₀. Если же электрон находится на более низком уровне (ниже штриховой линии) и поглощает фотон той же энергии, то энергия электрона вне ме­талла будет меньше К_макс.

W₀=A_{вых ,-} работа выхода, К_макс =,поэтому

формулу (1) часто записывают в виде

(3)

Из (3) вытекает, что в случае, когда работа выхода превышает энергию кванта, электроны не могут покинуть металл. Следовательно, для возникновения фотоэффекта, необходимо: , или

 частота ₀ или длина волны ₀ называется

красной границей фотоэффекта.