!Оптика и квантовая механика / Лекции / Лекции неизвестного авторства / набитые лекции / Лекция 08

Лекция 8.

На прошлой лекции мы рассмотрели поляризованный свет (свет, в котором колебания вектора напряженности электрического поля волны каким-либо образом упорядочены) и естественный свет (вектор напряженности электрического поля беспорядочно меняется со временем). Для того, чтобы получить из естественного света поляризованный, нужно пропустить его через поляризатор (устройство, которое пропускает колебания только одного направления).

Пусть на поляризатор падает естественный свет. На пути вышедшего из поляризатора света, у которого будет интенсивность и амплитуда , поставим еще один поляризатор, называемый анализатором, причем плоскости пропускания анализатора и поляризатора находятся под углом (см. рисунок). Посмотрим, как зависит интенсивность вышедшего из анализатора света от угла . Анализатор пропускает колебания вдоль его плоскости пропускания, а перпендикулярное этому направлению – не пропускает. Разложим вектор волны, вышедшей из поляризатора, на две составляющие, одна из которых параллельна плоскости пропускания анализатора, другая ей перпендикулярна. Тогда амплитуда волны, вышедшей из анализатора, находится по следующей формуле:

.

Поскольку в основном измеряется интенсивность, имеем:

Выражение носит название закона Малюса.

П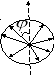осмотрим, что произойдет, если через поляризатор пропустить естественный свет. В естественном свете (см. рисунок) колебания различных направлений быстро и беспорядочно сменяют друг друга, т.е. за время детектирования угол может принимать любое значение. Поэтому чтобы определить интенсивность света, вышедшего из анализатора, мы должны выражения для закона Малюса усреднить по углу, получим , потому что, как известно, если время детектирования много больше периода, то среднее значение косинуса за это время равно . Тогда мы можем записать общую формулу:

,

где - интенсивность света, вышедшего из анализатора, - интенсивность естественного света, падающего на поляризатор, - угол между плоскостями пропускания поляризатора и анализатора.

Частично поляризованный свет.

Частично поляризованный свет – это свет, в котором колебания одного направления преобладают над колебаниями других направлений; его можно рассматривать как смесь линейно поляризованного и естественного света (см. рисунок). Если на пути такого света поставить поляризатор и вращать его, то интенсивность, очевидно, будет меняться, потому что когда плоскость пропускания поляризатора совпадет с направлением линейно поляризованной составляющей, интенсивность вышедшего света возрастет. Степенью поляризации называется следующее выражение:

,

где - максимальное значение интенсивности света, прошедшего через поляризатор, минимальное значение интенсивности света, прошедшего через поляризатор. Для плоско поляризованного света , . А для естественного света и степень поляризации = 0. В общем случае, свет является эллиптически поляризованным. При пропускании эллиптически поляризованного света через поляризатор интенсивность его, очевидно, будет меняться, циркулярно поляризованного – не будет меняться.

Поляризация света при отражении и преломлении.

Вспомним, что нам известно о законах отражения и преломления:

1. угол падения = углу отражения;

2. .

Первоначально эти законы были получены экспериментально, мы же сейчас получим эти законы теоретически.

Законы отражения и преломления света.

Формальная теория отражения и преломления света строится на основе граничных условий, которым удовлетворяют векторы поля на границе раздела двух сред. Если на поверхности границы раздела нет поверхностных зарядов и токов, что соответствует физика процесса, который в данный момент изучаем, то граничные условия, известные нам из курса электричества выглядят следующим образом:

Вообще говоря, все эти условия были выведены для случая постоянных полей, однако они справедливы и для случая переменных полей (это можно показать при помощи уравнения Максвелла в интегральной форме). Обозначим индексами «0» - падающий свет, «1» - отраженный свет, и «2» - преломленный свет. Тогда из граничного условия следует выражение:

Аналогичное выражение получаем для вектора . Чтобы выражение выполнялось для произвольного момента времени, необходимо, чтобы (чтобы можно было сократить на ). Здесь - вектор, начало которого может быть где угодно, но оканчивается этот вектор в точке на границе раздела. Чтобы выражение выполнялось для любой точки границы раздела, необходимо:

1. должны лежать в одной плоскости – плоскости падения ZX. Иначе мы пройдем по перпендикуляру к плоскости, в которой лежат 2 вектора, там (на перпендикуляре) будет ненулевой вклад третьего вектора. Получится, что в одной точке этот вклад существовать будет, а в других – нет. (???)

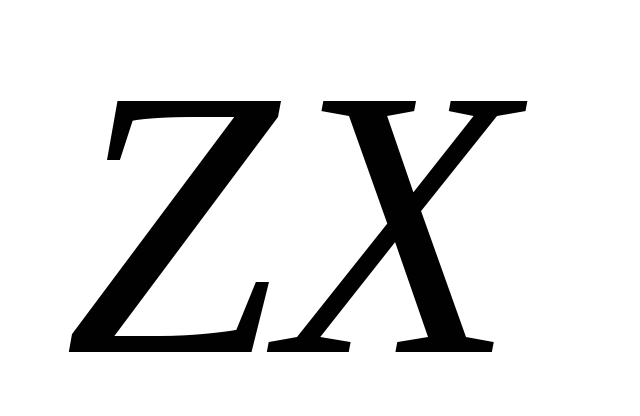
2. мы находимся в плоскости падения и идем по границе раздела, где , тогда коэффициенты при х в показателях экспонент в выражении должны быть одинаковы, т.е.

Формулы Френеля.

Помимо законов отражения и преломления, из записанных выше граничных условий можно определить амплитуды и состояния поляризации для преломленной и отраженной волн, если эти характеристики известны для падающей волны. Разложим волны 0, 1 и 2 на 2 составляющие, одна из которых поляризована в плоскости падения, другая – в направлении перпендикулярном плоскости падения:

Условимся для Е и Н в каждой из волн выбрать положительное направление, обозначенное на рисунке:

Очевидно, .

На границе раздела все экспоненциальные множители в уравнении предыдущего параграфа были одинаковы (при фиксированной координате х и в фиксированный момент времени), тогда граничные условия примут вид: (сократим на экспоненту):

В плоской волне векторы и связаны следующим соотношением (уравнение Максвелла):

Покажем, что в нашем случае .

Для волны вида справедливы следующие выкладки:

1) ;

2) , т.к. .

Рассмотрим выражения для ротора:

.

Учитывая все вышесказанное, получим:

Обычно в диэлектриках , тогда

Заметим, что , тогда из предыдущего выражения следует, что

.

В результате получаем следующую систему для падающей, отраженной и преломленной волн:

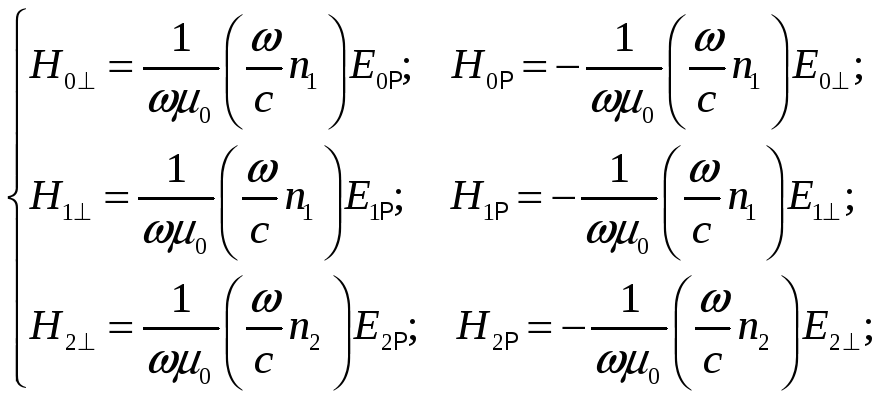
В уравнениях и (касательный вектор) можно брать как вдоль , так и вдоль оси х:

1) в случае , ;

2) в случае , , т.е. .

Т.е. из уравнения получили следующую систему уравнений:

То же самое можно получить из уравнения , точно так же используя систему :

Получили систему из 4 уравнений + . Ее можно разрешить относительно компонент отраженной и преломленной волн, выразив их через компоненты падающей волны. Следующие формулы , где это самое и проделано, называются формулами Френеля:

Следствие 1.

При нормальном падении и (при переходе от синусов к углам)

.

То есть при , векторы падающего и отраженного света на границе раздела совершают колебания в противофазе - происходит потеря полуволны при отражении от оптически более плотной среды (знак « – » - фаза меняется на , а разность хода – на ). Если , то потери полуволны не происходит.

Если падающая волна поляризована по (в направлении перпендикулярном плоскости падения), то потеря полуволны происходит не только при перпендикулярном падении (см. формулу ), а при произвольном угле. Действительно, в случае, если свет идет из оптически менее плотной среды в оптически более плотную (), то . Для тонких пленок условие потери полуволны выполняется в общем случае.

Следствие 2.

Имеется значение угла падения, называемое углом Брюстера, определяемое из условия:

, ,

при котором , т.е. отраженная волна поляризована в направлении, перпендикулярном плоскости падения. Найдем значение этого угла:

.

Используя закон преломления, получим:

.

Для стекла угол Брюстера равен . При падении естественного света под углом Брюстера отразится только составляющая, поляризованная перпендикулярно плоскости падения, т.е. отраженный свет будет полностью линейно поляризован. Если же падающая под углом Брюстера волна поляризована в плоскости падения, то отраженной волны вообще не будет.

5