Сферические функции.

Оператор Лапласа в сферических кординатах

- угловая часть оператора Лапласа

Рассмотрим задачу Ш-Л на единичной сфере.

Определение. Дважды непрерывно дифференцируемые ограниченные на единичной сфере решения этой задачи называются сферическими функциями.

Ищем решение в виде , тогда для :

Тогда

Для функции

Это задача для присоединённых функций Лежандра, следовательно

Выпишем систему сферических функций n-го порядка

Квадрат нормы

Шаровые функции

Рассмотрим уравнение Лапласа в шаре

Учитывая , то для радиальной части

Это уравнение Эйлера

Решение которого ищется в виде

Первая и вторая формулы Грина.

Напомним формулу Гаусса-Остроградского.

Введём оператор

Рассмотрим интеграл

Учитывая, что

Формула называется первой формулой Грина

Поменяв местами u и v

Вычитая, получаем

-Вторая формула Грина.

В частном случае, когда

В трёхмерном случае введём сферическую систему координат с центром в токе . Найдём решение уравнения Лапласа зависящее только от расстояния до -

Решение называется фундаментальным решением для уравнения Лапласа.

В двумерном случае

фундаментальное решение удовлетворяют уравнению во всех точках кроме

Третья формула Грина

Пусть

Поскольку в области то переходя к пределу

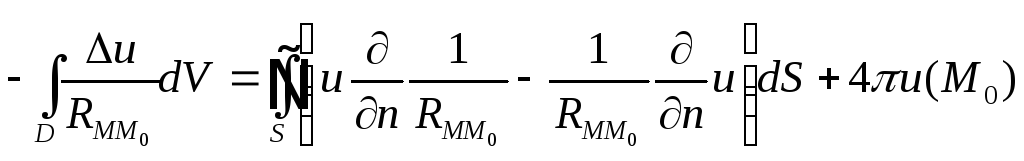
Или

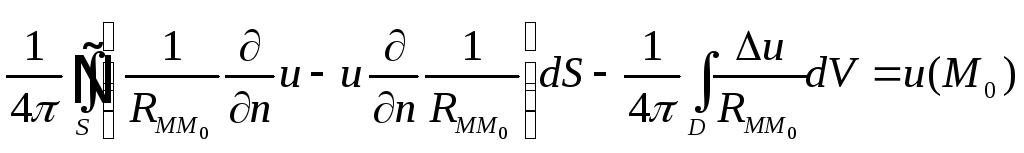
Действуя по этой схеме, окончательно получим

Замечание

Основные свойства обобщённых функций

1. Если - гармоническая функция в области D, то

Доказательство. Положим во второй формуле Грина.

2. Теорема о среднем

Доказательство. Применяем 3-ю формулу к шару и учитываем первое свойство.

3. Гармоническая в области D функция имеет внутри D производные всех порядков

Это утверждение следует из 3 формулы Грина, так интегралы собственные и их можно дифференцировать, сколько угодно раз.

4. Принцип максимума. Гармоническая в области D функция , непрерывная в замкнутой области , достигает своих максимальных и минимальных значений на границе области D.

Внутренние краевые задачи

Внутренняя задача Дирихле

Определение Классическим решением внутренней задачи Дирихле

называется функция , непрерывная в замкнутой области , удовлетворяющая уравнению в области D и непрерывно примыкающая к заданным граничным значениям

Теорема Задача Дирихле не может иметь более одного классического решения.

Вопрос о существовании будет рассмотрен позже.

Третья краевая задача.

Теорема. Пусть на , причём . Тогда 3-я краевая задача (n- внешняя нормаль к D) не может иметь более одного классического решения.

В силу линейности задачи достаточно показать, что однородная краевая задача.

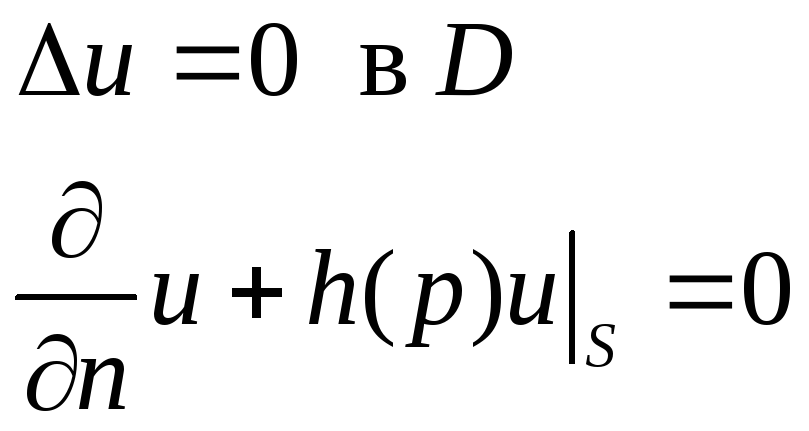
имеет только нулевое решение.

Используя первую формулу Грина .

т.к. в ,

следовательно, в D, а в тех точках поверхности где , отсюда следует, что .

Внутренняя задача Неймана.

Необходимым и достаточным условием разрешимости задачи Неймана является , где

Внешние краевые задачи

Функции регулярные на бесконечности.

Для функций регулярных на бесконечности справедливы 1-я, 2-я и 3-я формулы Грина.

Можно показать, что если гармоническая функция 0 при