Лекция 3. Специальные функции.

В предыдущей лекции мы рассмотрели некоторые физические задачи, приводящие к уравнениям в частных производных, а так же обсудили их классификацию. Уравнения каждого типа обладают рядом специфических свойств. Однако существуют и общие методы решения применимые для уравнения всех типов. Один из таких методов – метод разделения переменных или метод Фурье. Прежде чем изложить метод разделения переменных решения начально-краевых задач, при котором естественно возникает необходимость рассмотрения специальных функций, являющихся решением задач Штурма-Лиувиля, изучим свойства наиболее часто встречающихся спец.функций.

1. Цилиндрические функции.

Уравнением Бесселя или уравнением цилиндрических функций, называется уравнение вида

(1)

Это уравнение может быть записано и в другой эквивалентной форме

.

Напомним свойства гамма-функции.

Гамма-функцией называется интеграл

- комплексное число, реальная часть которого положительна.

а) , .

б) , если -натуральное число, то

в)

Решение уравнения Бесселя можно искать в виде обобщённого степенного ряда

Подставляя это выражение в уравнение (1) и приравнивая коэффициенты при одинаковых степенях , получим следующие рекуррентные соотношения

Из первого уравнения следует, что , рассмотрим случай , тогда

Выберем в виде

тогда

Рассмотрим ряд

(2)

Это ряд в силу признака Даламбера абсолютно сходится для любых .

Определение. Ряд (2) называется функцией Бесселя порядка .

очевидно является частным решением уравнения (1).

Если и не является целым числом, то проделав аналогичные выкладки получим

Определение. Ряд называется функцией Бесселя порядка .

Рекуррентные формулы.

Прямой проверкой легко убедится в справедливости соотношений

Частный случай

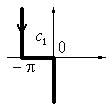
Определение. Функциями Ханкеля первого и второго рода называются функции, определяемые интегралами

,

г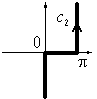 де контуры интегрирования имеют вид изображённый на рисунке

Для функций Ханкеля справедливы рекуррентные соотношения аналогичные рекуррентным соотношениям для функции Бесселя

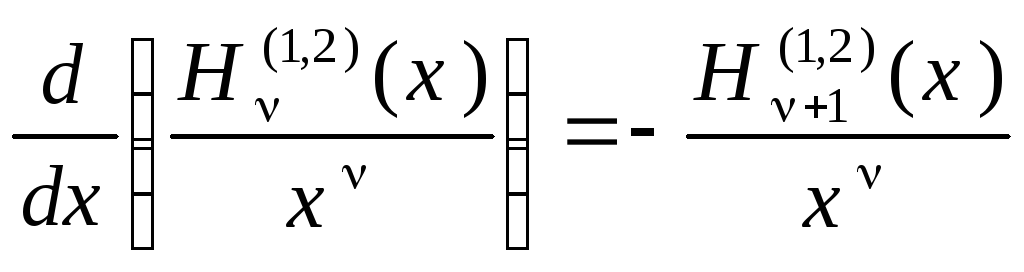
Приведём без доказательства ещё одну важную формулу

Определение. Функция

называется функцией Неймана.

Используя это определение, получим

Теорема. Функции Бесселя и Ханкеля линейно независимы.

Схема доказательства. Достаточно доказать, что определитель Вронского отличен от нуля.

Цилиндрические функции чисто мнимого аргумента

Определение. Функция

называется функцией Инфельда.

Замечание. Очевидно при вещественном положительном Функция Инфельда принимает вещественные значения.

Определение. Функция

Называется функцией Макдональда.

Функция Макдональда также является действительной функцией при положительном

Общее решение уравнения

может быть записано в виде

Общее решение уравнения

может быть записано в виде

Полиномы Лежандра.

Краевая задача для полиномов Лежандра имеет вид

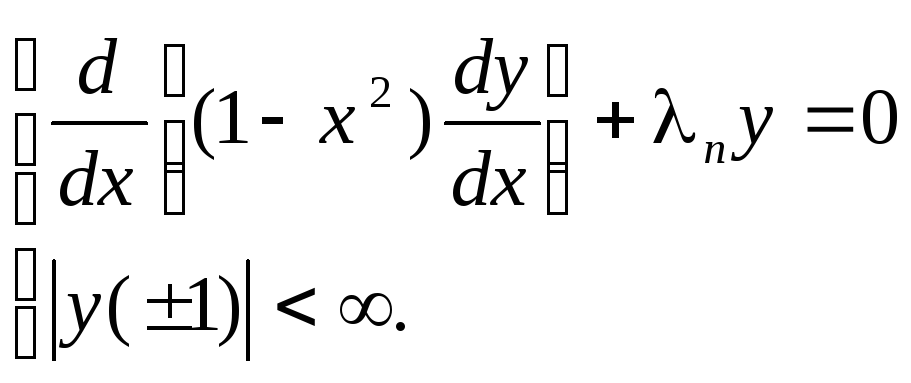
Собственные значения . Сами полиномы Лежандра определяются с помощью Формулы Родрига

Предъявим также выражение для нормы полиномов Лежандра

Отметим ещё одну важную формулу

Функция носит название производящей функции для полиномов Лежандра.

Теорема Стеклова (для полиномов Лежандра). Всякая дважды непрерывно дифференцируемая на отрезке [-1,1] функция разложима в абсолютно и равномерно сходящийся ряд по полиномам Лежандра.

,

где

Выпишем первые пять полиномов

Присоединённые функции Лежандра.

Определение. Присоединёнными функциями Лежандра называются функции, определённые соотношением

Заметим, что для присоединенных функций Лежандра имеет место формула ортогональности по нижнему индексу

Задача Штурма-Лиувиля имеет вид

,

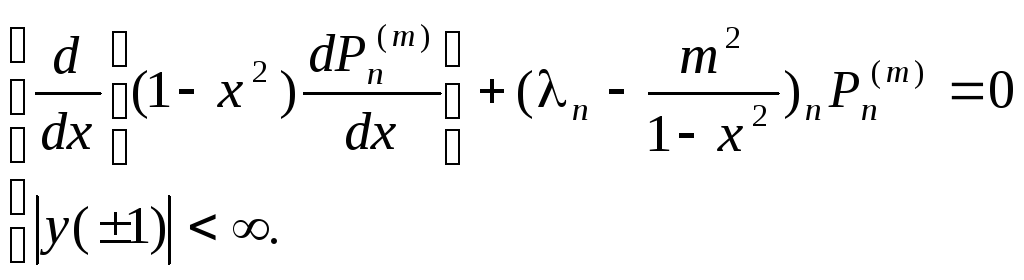В силу общих свойств собственных свойств, для присоединенных функций Лежандра имеет место теорема разложимости Стеклова.

Теорема. Всякая функция , дважды непрерывно дифференцируемая на отрезке [-1,1] и обращающаяся в нуль на его концах , разлагается в абсолютно и равномерно сходящийся по присоединённым функциям Лежандра (m=0):

где коэффициенты Фурье равны

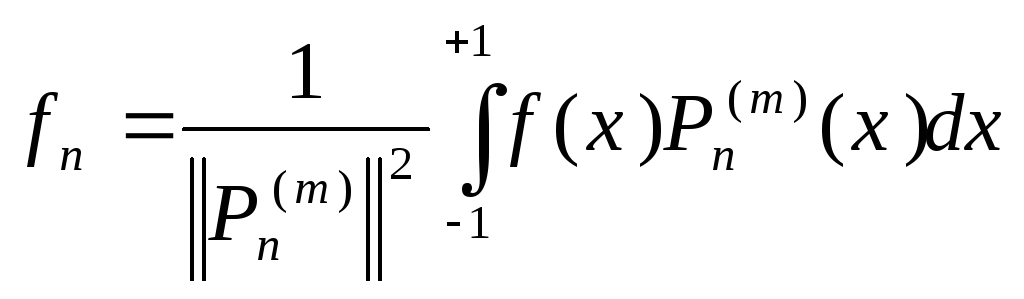
где квадрат нормы может быть вычислен с помощью интегрирования по частям.

Сферические функции.