Лекция 1. Уравнения в частных производных первого порядка.

Введение.

Различные физические явления описываются дифференциальными уравнениями в частных производных:

- уравнение теплопроводности,

- уравнение колебаний,

- уравнение Лапласа и т. д.

Различным методам интегрирования уравнений в частных производных второго порядка и посвящён наш курс лекций. Но прежде чем перейти к этим задачам рассмотрим методы интегрирования уравнений в частных производных первого порядка, теория которых тесно связана с интегрированием некоторых систем обыкновенных дифференциальных уравнений. Приведём несколько простейших примеров.

Пример 1.

,

интегрируя по

,

где - произвольная функция переменой .

Пример 2.

Сделаем замену 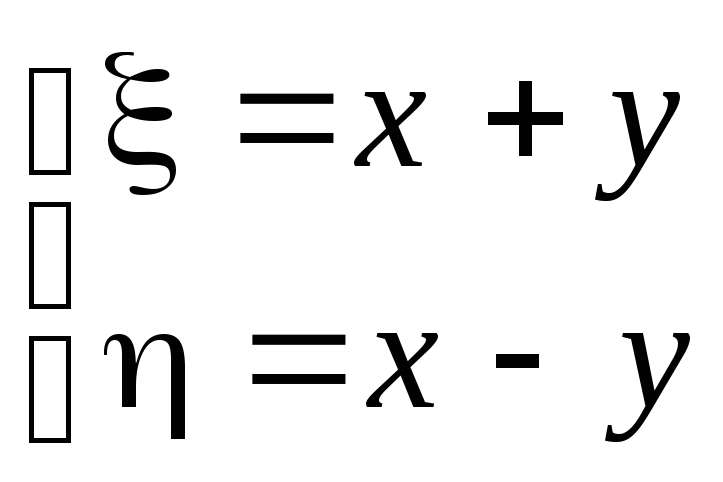, тогда , , а так как , то , а . Исходное уравнение преобразуется к виду;

интегрируя по переменной , получим:

.

§ 1. Квазилинейные уравнения в частных производных первого порядка.

Определение. Квазилинейным уравнением первого порядка в частных производных называется уравнение вида:

Это уравнение линейно относительно производных, но может быть нелинейным относительно неизвестной функции .

Рассмотрим вначале квазилинейное уравнение с двумя независимыми переменными.

(1)

Составим систему обыкновенных дифференциальных уравнений:

Пусть и два независимых интеграла этой системы.

Теорема 1. Общее решение уравнения (1) может быть записано в виде

,

где произвольная функция.

Доказательство. Уравнение (1) можно интерпретировать как скалярное произведение векторов и , где первый вектор есть нормаль к поверхности , если же эта поверхность задана неявно , то условие ортогональности нормали и вектора приобретает вид:

(2)

Следовательно, для решения уравнения (1) достаточно проинтегрировать уравнение (2). Пусть некоторое решение (2) покажем, что , но

Так как мы предполагаем, что P, Q и R одновременно не обращаются в ноль, то приходим к выводу, что определитель этой системы

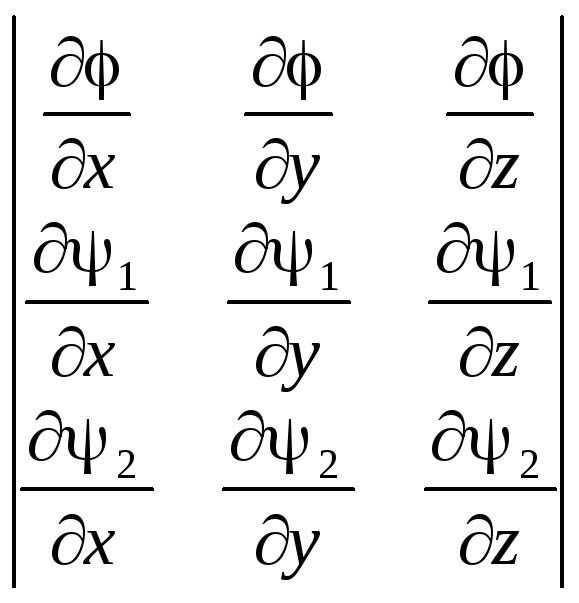
тождественно равен нулю в рассматриваемой области. Но тождественное обращение в ноль якобиана указывает на наличие функциональной зависимости между этими функциями, т.е. , но из независимости и немедленно следует, что .■

Чтобы найти поверхность , удовлетворяющую дифференциальному уравнению (1) и проходящую через данную линию:

надо в найденные первые интегралы

(3)

подставить вместо их выражения через параметр . Получится два уравнения вида

(4)

Исключив из них , получим соотношение , подставив вместо , левые части из (3) получим искомое решение.

В том случае, когда в оба уравнения (4) не входят , тогда заданная линия является характеристикой системы и задача Коши имеет бесконечно много решений.

Пример 3. Найти общее решение уравнения

А также интегральную поверхность, проходящую через данную линию , .

Решение. Составляем систему уравнений

и находим её первые интегралы , , следовательно, общее решение можно записать в неявном виде , т.к. входит только в один из первых интегралов, то решение можно записать в явном виде . Чтобы найти поверхность проходящую через линию нужно поставить параметрическое задание линии в первые интегралы, взяв в качестве параметра

Исключив получим подставляя сюда вместо констант соответствующие им первые интегралы или .