Уравнение теплопроводности в неограниченной области.

(1)

Дадим определение классического решения

Определение. Классическим решением задачи (1) называется функция , определённая и непрерывная вместе со вторыми производными по и первыми производными по в области , удовлетворяющая уравнению (1) в этой области, непрерывная по в области и удовлетворяющая начальному условию.

Теорема. Задача (1) может иметь только одно классическое решение, ограниченное в .

Доказательство. Пусть два классических ограниченных решения задачи

. Очевидно есть решение задачи

И кроме того

Но воспользоваться принципом максимума в неограниченной области нельзя.

Чтобы воспользоваться принципом максимума, рассмотрим ограниченную по область . Здесь будем потом увеличивать.

Введём вспомогательную функцию

Эта функция удовлетворяет уравнению теплопроводности, кроме того

Применяем принцип сравнения к функциям и

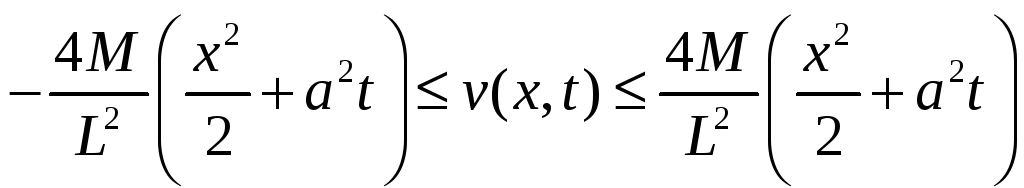
Это справедливо поэтому фиксируя и устремляя . Получим

Для решения задачи (1) применим преобразование Фурье с ядром

, ,

,

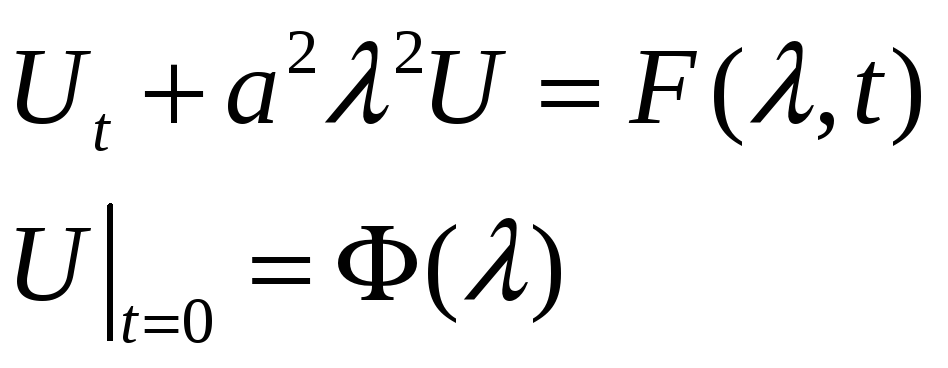
Вычислим интеграл в фигурных скобках

Обозначим

(2)

Теорема. Если непрерывна и ограничена на бесконечной прямой функция, а не прерывна по совокупности переменных и ограниченна, то формула определяет при классическое решение задачи (1).

Замечание требование ограниченности и непрерывности может быть ослабленно.

Доказательство теоремы на стр 218. Боголюбов Кравцов, Свешников

Задача для уравнения теплопроводности на полупрямой

Лемма. Пусть функция определена на бесконечной прямой , имеет на ней ограниченные производные до N-го порядка, и линейная комбинация

,

нечётна относительно точки .Тогда функция

Удовлетворяет условию

Прежде всего отметим, что функция Грина

удовлетворяет условию

В силу наложенных на условий интеграл можно дифференцировать

Интегрируя по частям, получим

и в силу нечётности всей! Подынтегральной функции при , получаем .

Способ решения однородного уравнения теплопроводности

Продолжим , заданную при , на всю действительную ось, построив функцию , которая удовлетворяет условиям .

Теперь решим задачу Коши на прямой.

Очевидно, это решение будет решением на полупрямой.

Задача Дирехле

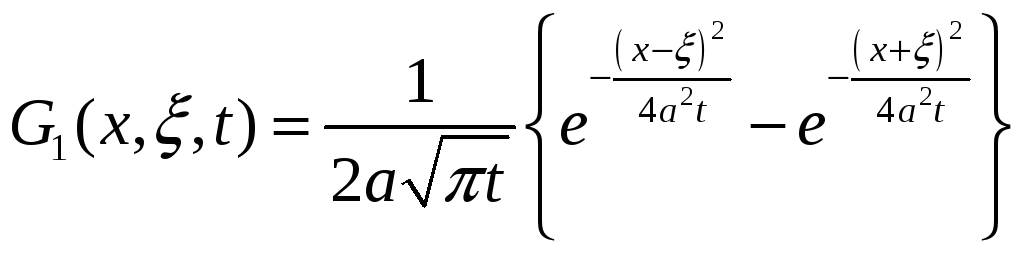
Решение неоднородной задачи

Для задачи Неймана

Неоднородное граничное условие

Используем синус преобразование Фурье.

4