Постановка начально-краевой задачи для уравнений колебаний

Определение. Классическим решением начально-краевой задачи называется функция непрерывная вместе с первыми производными в замкнутом цилиндре, имеющая непрерывные производные второго порядка в открытом цилиндре, удовлетворяющая уравнению, начальным и граничным условиям.

Теорема. Задача может иметь только одно классическое решение

Доказательство.

Пусть -два различных классических решения

В силу линейности функция является решением следующей однородной начально-краевой задачи

Построим интеграл

Покажем, что интеграл не меняется во времени

Воспользуемся первой формулой Грина

и подставим в предыдущее соотношение

Для первой и для второй задачи из начальных условий

Для третьей

Отсюда

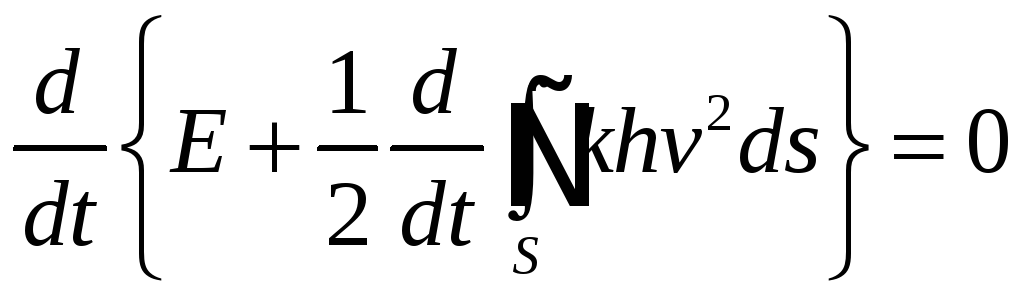
из начальных условий

Итак, для всех случаев и учитывая начальные условия

Формальное построение решения

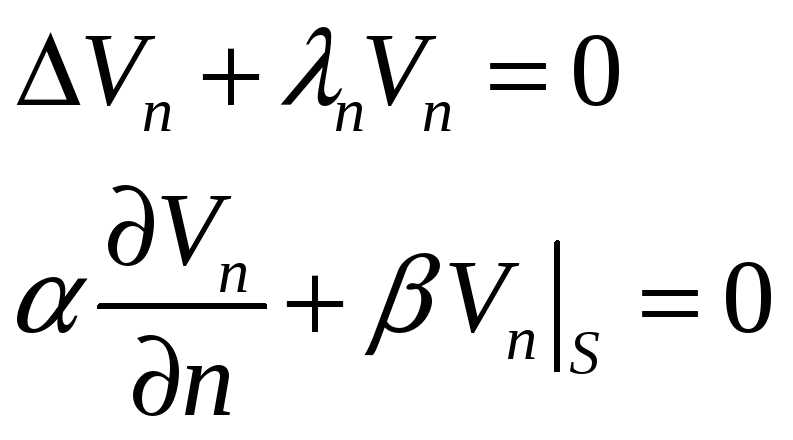
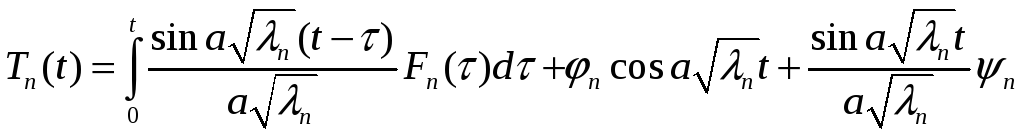
Формула Даламбера

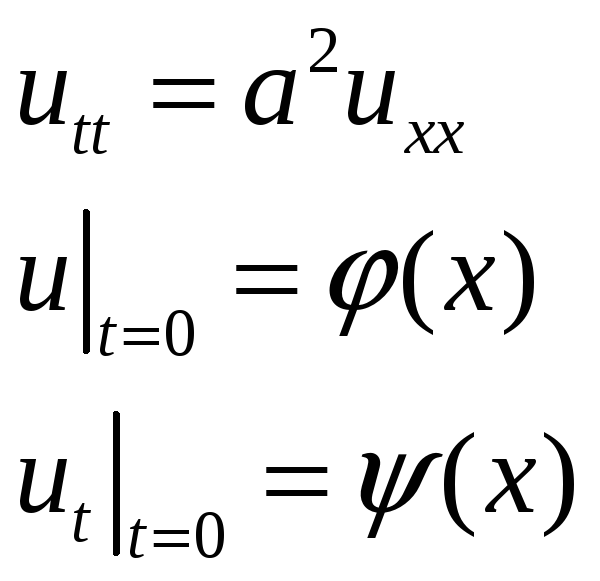
Сделаем замену переменных

Для определения неизвестных функций

последнее равенство можно записать

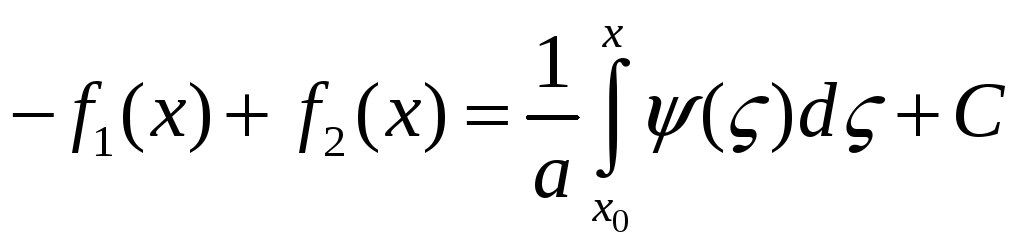
Вычитая и складывая

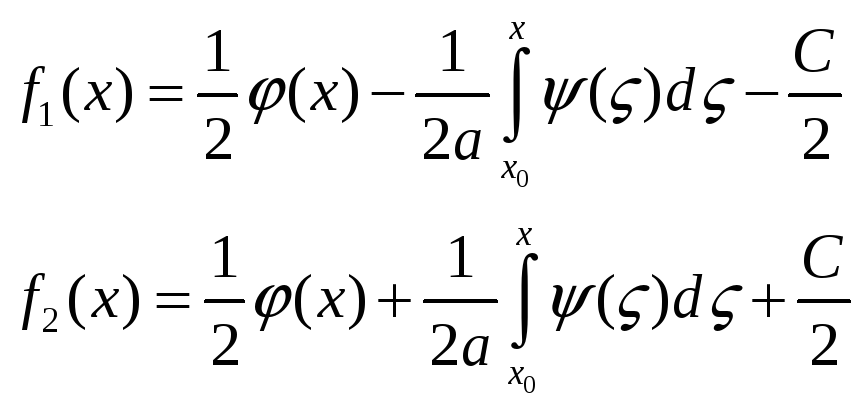
И окончательно

Рассмотрим задачу для неоднородного уравнения колебаний на прямой с однородными начальными условиями.

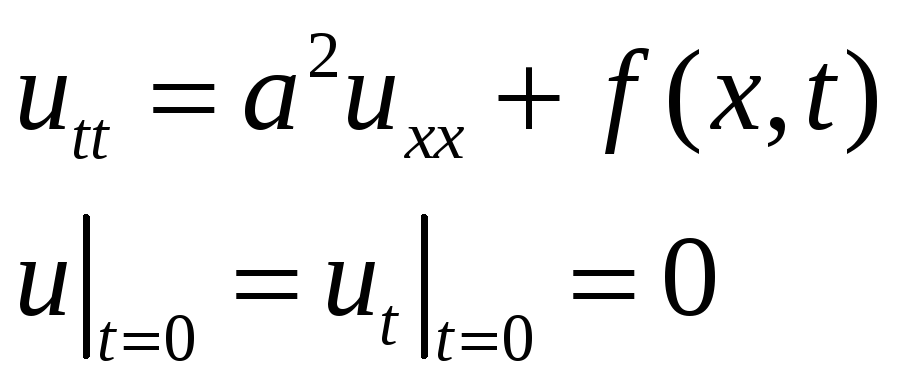
Для решения задачи применим преобразование Фурье

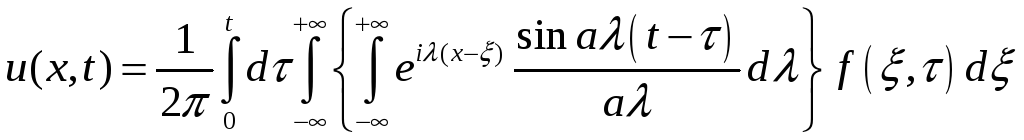
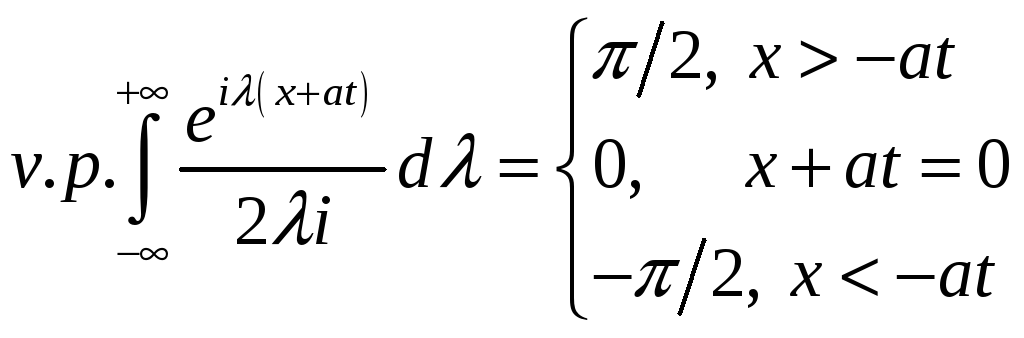
В случае лемма Жордана справедлива в верхней полуплоскости поэтому контур замыкается в положительном направлении т.е. против часовой стрелки

В случае замыкать контур нельзя однако интеграл от нечётной функции в симметричных пределах .

В случае лемма Жордана справедлива в нижней полуплоскости поэтому контур замыкается по часовой стрелки в нижнюю полуплоскость.

!!!!!!!!!!! полюс первого порядка лежит на контуре следовательно надо учитывать только полвычета. Аналогично

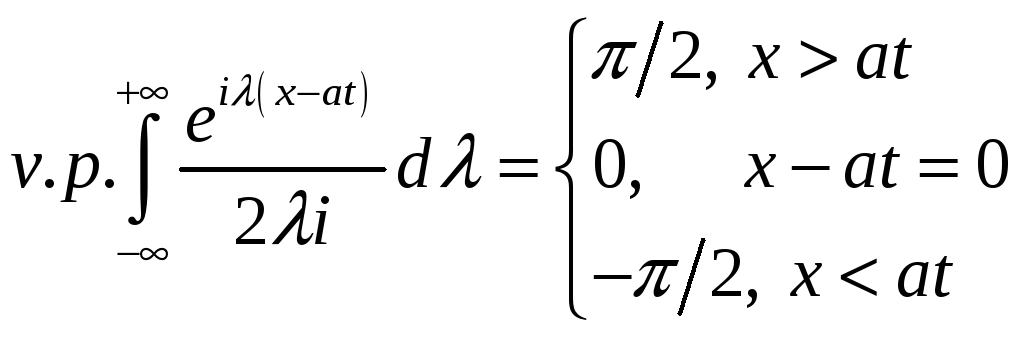
Окончательно получаем

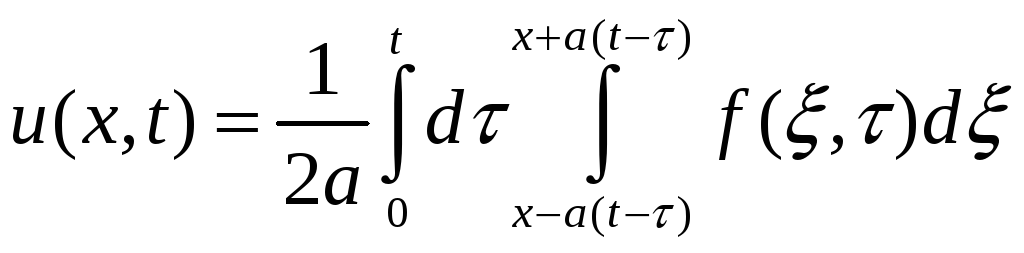
Таким образом, если у нас есть и начальные и граничные условия

.

Полупрямая

Лемма. Пусть функции определена на бесконечной прямой , имеет на ней ограниченные производные до N-го порядка, и линейная комбинация

,

нечётны относительно точки . Тогда функция

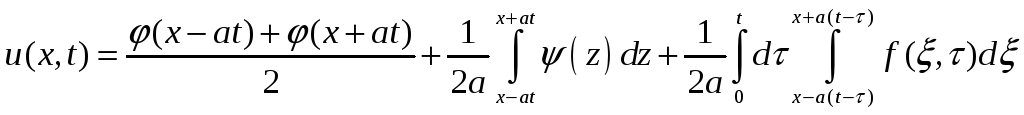
Удовлетворяет условию

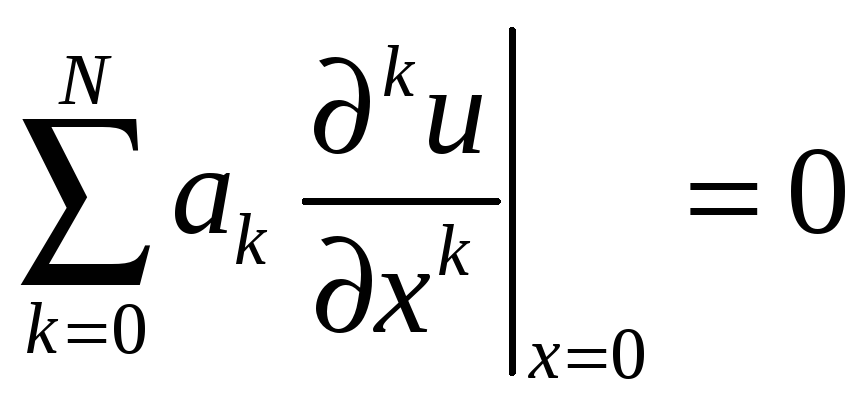
Задача Дирихле

Метод распространяющихся волн

Второе граничное условие также удовлетворяется

обозначим аргумент через z