Постановка начально-краевой задачи для уравнений колебаний

Определение. Классическим решением начально-краевой задачи называется функция непрерывная вместе с первыми производными в замкнутом цилиндре, имеющая непрерывные производные второго порядка в открытом цилиндре, удовлетворяющая уравнению, начальным и граничным условиям.

Теорема. Задача может иметь только одно классическое решение

Доказательство.

Пусть -два различных классических решения

В силу линейности функция является решением следующей однородной начально-краевой задачи

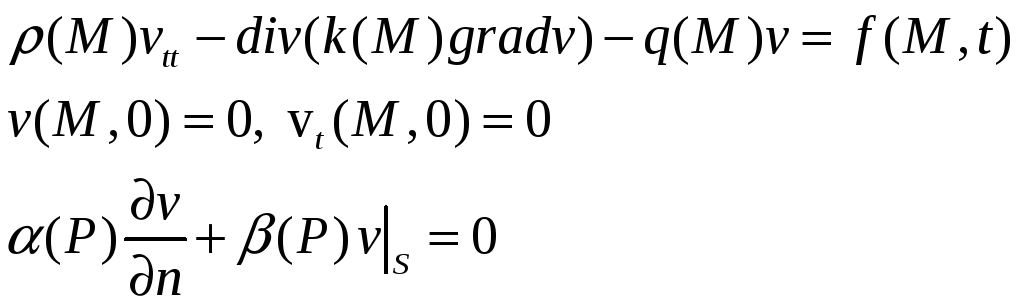
Построим интеграл

Покажем, что интеграл не меняется во времени

Воспользуемся первой формулой Грина

и подставим в предыдущее соотношение

Для первой и для второй задачи из начальных условий

Для третьей

Отсюда

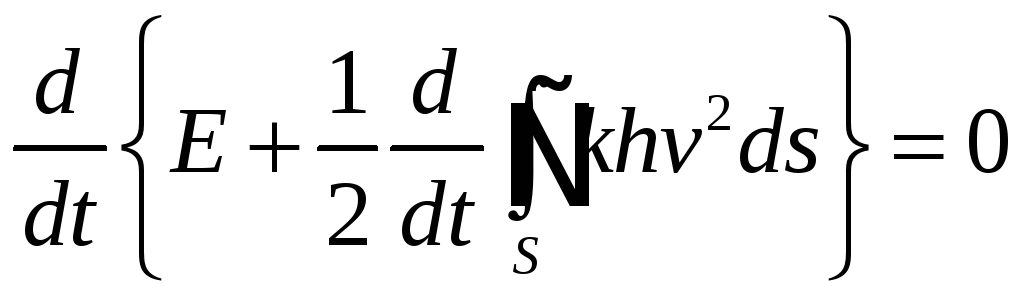
из начальных условий

Итак, для всех случаев и учитывая начальные условия

Формальное построение решения

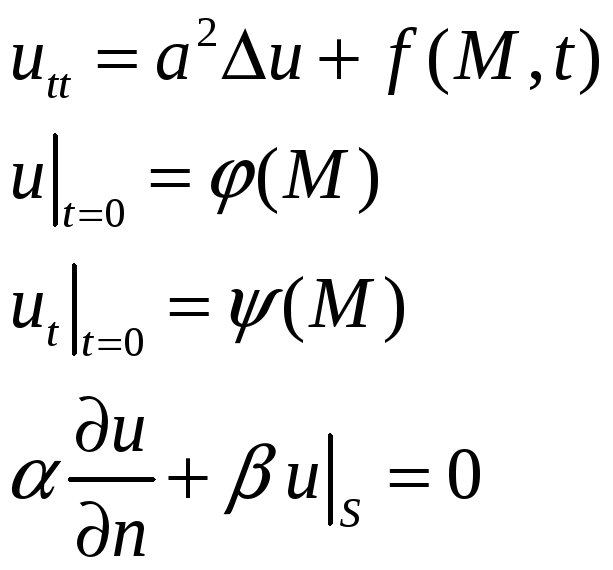
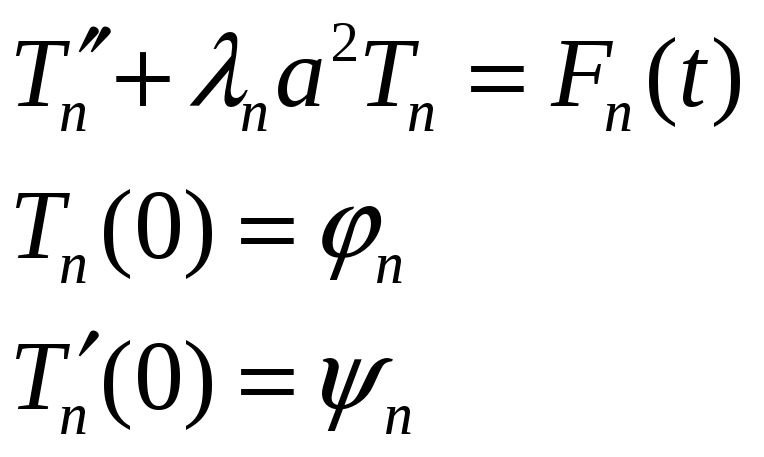
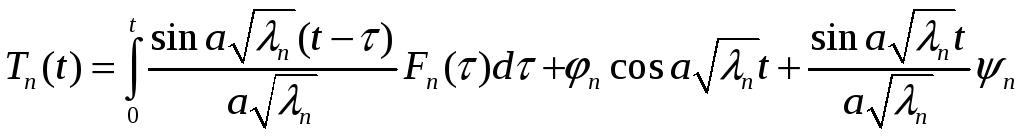
Формула Даламбера

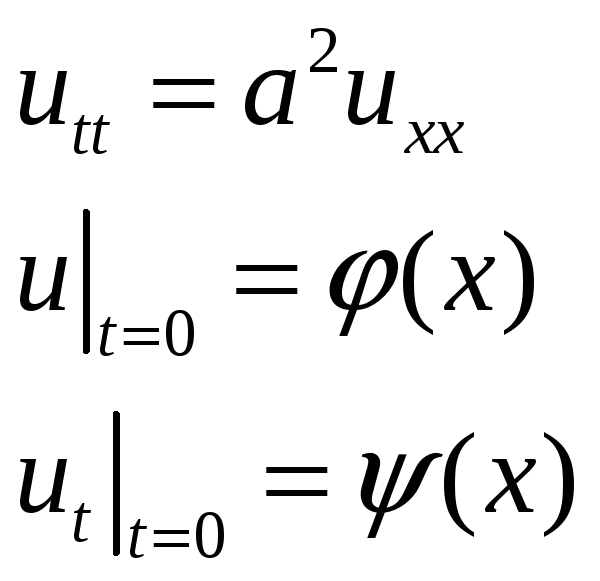
Сделаем замену переменных

Для определения неизвестных функций

последнее равенство можно записать

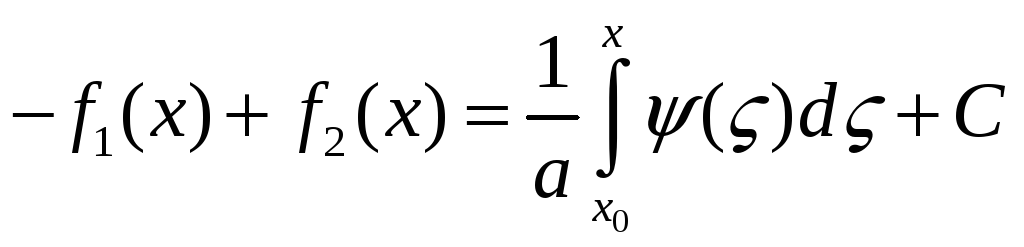
Вычитая и складывая

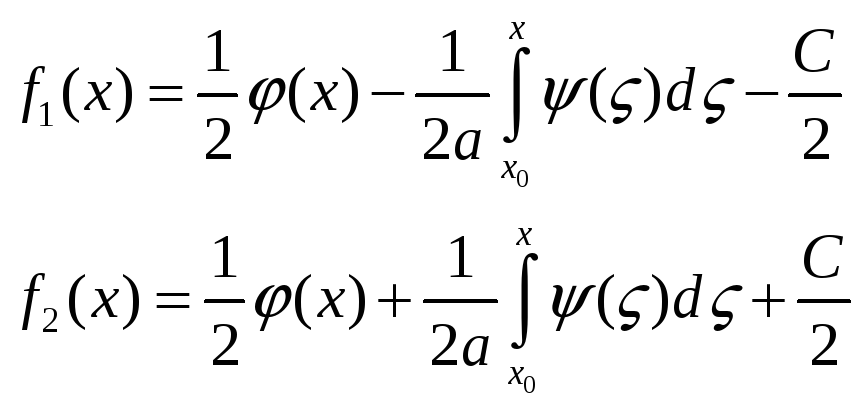
И окончательно