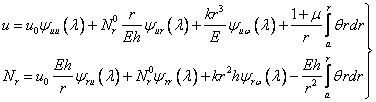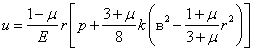диски расчет 2

Диск с центральным отверстием

 

Для дисков постоянной толщины при , можно получить замкнутое решение задачи.

При решении системы уравнений (1.1) - (1.3), (1.7), (1.8) применяем метод начальных параметров. Согласно этому методу по­стоянные интегрирования выражаем через начальные параметры  и  - радиальное перемещение и радиальное усилие, соответствующие внутреннему контуру диска.

Из уравнений (1.7) и (1.8) вытекает, что

 

(2.1)

 

Подставляя выражение (2.1) в уравнение (1.1), получаем

 

(2.2)

 

Интегрируя уравнение (2.2) в промежутке от  до текущего значения , находим

 

(2.3)

 

(2.4)

 

Подставляем выражение (2.3) в первое уравнение системы (1.12):

 

(2.5)

 

Принимая во внимание, что , получаем

 

(2.6)

 

Интегрируем уравнение (2.6) в промежутке от  до :

 

(2.7)

 

Подставляя в уравнение (2.7) выражение (2.4) для , получаем

 

(2.8)

 

Подставляя выражение (2.8) в уравнение (2.3), находим

 

(2.9)

 

Введем обозначения:   и

 

,	,
,	,
,	.

 

Тогда уравнения (2.8) и (2.9) можно записать в следующем виде:

 

(2.10)

 

Уравнения системы (2.10) являются основными при расчете дис­ков постоянной толщины с нейтральным отверстием. Начальные пара­метры ,  определяем из граничных условий (1.22), (1.23).

Функции , , , ,,   называются сопровождающими функциями для диска. Их числовые значения для  приведены в приложении.

Сплошной диск

 

Для дисков постоянной толщины при , можно получить замкнутое решение задачи.

Основные уравнения для диска без центрального отверстия полу­чаем из уравнений (2.8) и (2.9), выполняя в этих уравнениях пре­дельный переход при и принимая во внимание, что для сплош­ного диска , .

Предварительно находим, используя соотношение (1.33),

 

(2.11)

 

Переходя к пределу при  в уравнениях (2.8) и (2.9), по­лучаем с учетом выражения (2.11):

 

(2.12)

 

(2.13)

 

Уравнения (2.12) и (2.13) является основным при расчете сплошных дисков. Они содержат только один начальный параметр , который можно определить из граничного условия на наружном конту­ре диска:. Из этого условия с учетом выражения (2.13) находим

 

(2.14)

 

Напряжения и деформации в сечениях диска при  находим по формулам  (1.13), в центре диска - по формулам (1.41).

Рассмотрим более подробно случай, когда неравномерный нагрев диска отсутствует . В этом случае , .

Подставляя значение начального параметра  в уравнения (2.12) а (2.13), находим

 

(2.15)

 

(2.16)

 

Подставляя выражения (2.15) и (2.16) в уравнение (1.13) для кольцевого усилия  при , получаем

 

(2.17)

 

 

Рис. 2.1. Графики напряжений во вращающемся сплошном диске при отсутствии нагрева

 

Формулы для напряжений в диске имеют вид:

 

(2.18)

 

(2.19)

 

Графики напряжений,  построенные  по  зависимостям  (2.18)  и (2.19), приведены на рис.2.1.  Наибольшие  напряжения возникают в центре диска

 

(2.20)

Пример расчета диска с центральным отверстием

 

Выполним расчет диска постоянной толщины  по сле­дующим данным:

 

– наружный радиус диска	;
– радиус центрального отверстия	;
– плотность материала диска	;
– модуль упругости	;
– коэффициент Пуассона материала диска
– угловая скорость вращения диска	;
– диск установлен на вал с натягом	;
– неравномерный нагрев диска отсутствует	;
– Интенсивность инерционной радиальной нагрузки, распределенной по наружной поверхности диска	.

 

Механические характеристики материала вала и диска одинаковы.

 

Расчет диска выполняем по уравнениям (2.10).

Динамический коэффициент .

Температурная деформация .

Начальные  параметры  и  определяем из граничных условий (1.19) и (1.23). Коэффициенты  и  находим по формулам (1.18) и (1.20). Принимая во внимание, что в данном случае , получаем

 

,

 

.

 

Граничное условие  (1.19)  принимает вид:

 

(2.21)

 

Из граничного условия (1.23) с учетом выражения (2.10) для  при  и  получаем

 

(2.22)

 

Подставляя в выражение (2.22) значения сопровождающих функций , ,  из табли­цы, приведенной в приложении, получаем следующее уравнение:

 

.

 

Решая систему уравнений (2.21) и (2.23), находим

 

,

.

 

Дальнейший расчет выполняем по формулам (2.10) и (1.13) при  для ряда кольцевых сечений диска. Значения сопровождающих функций принимаем по таблице, приведенной в приложении. Результа­ты расчета сводим в табл.2.1.

 

Таблица 2.1

Результаты расчета диска

,		,	,	,	,	,
50	1	0,0493	-420	19594	-4,20	195,24	-3,15	9,86
75	0,66	0,0467	4729	13862	47,29	138,62	0,29	6,22
100	0,50	0,0489	6146	11629	61,46	116,29	1,33	4,89
125	0,40	0,0527	6374	10348	63,74	10З,48	1,69	4,22
150	0,33	0,0568	6044	9391	60,44	93,91	1,61	3,79
175	0,29	0,0606	5372	8541	53,72	85,41	1,40	3,46
200	0,25	0,0636	4449	7710	44,49	77, Ю	1,07	3,19
225	0,22	0,0659	3317	6852	33,17	68,52	0,63	2,93
250	0,20	0,0668	2000	5947	20,00	59,47	0,11	2,67

 

На рис.2.2 приведены графики напряжений в диске, построенные по результатам расчета.

 

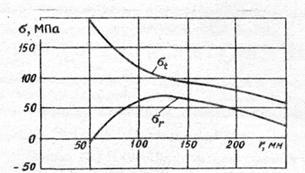
Рис.2.2. Графики напряжений во вращающемся диске с центральным отверстием при 

 

Анализ результатов расчета показывает, что наибольшее эквива­лентное напряжение имеет место у внутренней поверхности диска. По теории наибольших касательных напряжений эквивалентное напря­жение в точках внутреннего контура диска достигает значения

 

 МПа.