
диски расчет 3
.docЧисленный метод решения задачи о расчёте вращающихся неравномерно нагретых дисков переменной толщины
В разд. 1 было установлено,
что задача о расчете вращающегося
неравномерно нагретого диска переменной
толщины с центральным отверстием
сводится к интегрированию системы
дифференциальных уравнений (1.12) с
переменными коэффициентами в интервале
![]() при
заданных граничных условиях (1.22) и
(1.23). Эта, так называемая, краевая задача
(граничные условия сформулированы в
точках
при
заданных граничных условиях (1.22) и
(1.23). Эта, так называемая, краевая задача
(граничные условия сформулированы в
точках
![]() и
и
![]() интервала
интегрирования) в общем случае может
быть решена численным методом с
применением ЭВМ.
интервала
интегрирования) в общем случае может
быть решена численным методом с
применением ЭВМ.
Расчеты с применением ЭВМ имеют ряд характерных особенностей. В частности, при реализации численных методов расчета на ЭВМ весьма эффективным оказывается использование матричной формы записи машинных алгоритмов. Применение матричной символики позволяет не только компактно записать уравнения и алгоритм решения задачи, но и облегчить процесс программирования, так как ЭВМ, как правило, снабжены стандартными программами для матричных операций.
Из величия
![]() и
и
![]() составим
вектор
составим
вектор
 ,
который будем называть вектором
состояния, и запишем систему уравнений
(1.12) в матричной форме:
,
который будем называть вектором
состояния, и запишем систему уравнений
(1.12) в матричной форме:
|
|
|
(3.1) |
где
|
|
|
(3.2) |
|
|
|
(3.3) |
Наиболее распространенным методом численного решения линейной краевой задачи является метод начальных параметров, позволяющий свести решение краевой задачи к решению последовательности задач Коши. Напомним, что в задаче Коши (начальной задаче) требуется найти частное решение системы дифференциальных уравнений, удовлетворяющее начальным условиям.
Общее решение
![]() системы
неоднородных линейных дифференциальных
уравнений (3.1) можно представить в виде
суммы какого-либо частного решения
системы
неоднородных линейных дифференциальных
уравнений (3.1) можно представить в виде
суммы какого-либо частного решения
![]() этой
системы и линейной комбинации двух
линейно-независимых решений
этой
системы и линейной комбинации двух
линейно-независимых решений
![]() ,
,
![]() системы
однородных дифференциальных уравнений
системы
однородных дифференциальных уравнений
|
|
|
(3.4) |
Таким образом, можно записать
|
|
|
(3.5) |
где
![]() ,
,
![]() ,
– постоянные интегрирования.
,
– постоянные интегрирования.
Вектор
![]() можно
найти, решая задачу Коши для системы
(3.1) при произвольных начальных условиях
можно
найти, решая задачу Коши для системы
(3.1) при произвольных начальных условиях
 .
.
Численное решение
задачи Коши выполняем методом Рунге-Кутта.
Делим интервал
![]() на
заданное число
на
заданное число
![]() частей
с шагом
частей
с шагом
![]() (рис.3.1).
Согласно методу Рунге-Кутта, который
относится к числу шаговых методов,
вектор состояния в каждой последующей
точке находим по формуле
(рис.3.1).
Согласно методу Рунге-Кутта, который
относится к числу шаговых методов,
вектор состояния в каждой последующей
точке находим по формуле
|
|
|
(3.6) |
![]() ,
,
![]() ,
,
![]() ,
,
![]() -
векторы, определяемые по формулам:
-
векторы, определяемые по формулам:
![]()
![]()
![]()
![]()
Таким образом, задавая
начальный вектор
![]() ,
находим затем последовательно векторы
,
находим затем последовательно векторы
![]() ,
,
![]() ,
… ,
,
… ,
![]() по
формуле (3.6).
по
формуле (3.6).

Рис. 3.1. Схема деления диска на участки
Векторы
![]() ,
,
![]() можно
найти, решив две задачи Коши для системы
однородных уравнений (3.4), задавая
начальные условия:
можно
найти, решив две задачи Коши для системы
однородных уравнений (3.4), задавая
начальные условия:


При выборе начальных
векторов
![]() ,
,
![]() следует
обеспечить их линейную независимость.
следует
обеспечить их линейную независимость.
Численное решение
задач Коши для системы (3.4) находим
методом Рунге-Кутта, вычисляя
последовательно векторы состояния в
точках
![]() ,
,
![]() ,
… ,
,
… ,![]()
![]() по формулам:
по формулам:
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
где
![]() -
векторы, определяемые по формулам:
-
векторы, определяемые по формулам:
|
|
|
|
|
|
|
|
|
|
|
|
Постоянные интегрирования
![]() и
и
![]() определяем
из граничных условий (1.22) в (1.23), принимая
во внимание, что соотношение (3.5)
выполняется для всех точек интервала
определяем
из граничных условий (1.22) в (1.23), принимая
во внимание, что соотношение (3.5)
выполняется для всех точек интервала
![]() ,
в том числе, и для точек
,
в том числе, и для точек
![]() и
и
![]() ,
т.е.
,
т.е.
|
|
|
(3.7) |
где
![]() и
и
![]() -
действительные векторы состояния на
внутреннем и наружном контурах диска.
-
действительные векторы состояния на
внутреннем и наружном контурах диска.
Запишем соотношения (3.7) в развернутом виде:
|
|
|
(3.8) |
Из векторных соотношений (3.8) можно получить следующие скалярные соотношения:
|
|
|
(3.9) |
Используя граничные
условия (1.22) и (1.23), получаем с учетом
соотношений (3.9) систему линейных
алгебраических уравнений относительно
![]() и
и
![]() :
:
|
|
|
(3.10) |
где
![]() .
.
Решая систему (3.10), находим постоянные интегрирования.
Для сокращения
объема вычислений при численном решении
рассматриваемой краевой задачи
целесообразно так назначить
начальные векторы
![]() ,
,
![]() ,
,
![]() ,
чтобы одна из постоянных интегрирования
заведомо обращалась в нуль.
,
чтобы одна из постоянных интегрирования
заведомо обращалась в нуль.
Систему (3.10) можно представить в следующем виде:
|
|
|
(3.11) |
Для того, чтобы
![]() при
любых значениях достаточно выполнения
следующих соотношений:
при
любых значениях достаточно выполнения
следующих соотношений:
|
|
|
(3.12) |
Выражение
![]() не
может одновременно обратиться в
нуль ввиду линейной независимости
векторов
не
может одновременно обратиться в
нуль ввиду линейной независимости
векторов
![]() ,
,
![]() .
.
Соотношения (3.12)
будут выполнены, если при
![]() принять
принять
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
т.е.
,
т.е.
|
|
|
(3.13) |
Если
![]() ,
то необходимо, чтобы
,
то необходимо, чтобы
![]() .
В противном случае из соотношения
(1.22) следует, что одновременно и
.
В противном случае из соотношения
(1.22) следует, что одновременно и
![]() ,
а это означает, что граничное условие
на внутреннем контуре диска обращается
в тождество и решение задачи становится
неопределенным.
,
а это означает, что граничное условие
на внутреннем контуре диска обращается
в тождество и решение задачи становится
неопределенным.
В случае, когда
![]() и
и
![]() ,
для выполнения соотношений (3.12) можно
принять
,
для выполнения соотношений (3.12) можно
принять
![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
т.е.
,
т.е.
|
|
|
(3.14) |
При указанном выборе
начальных векторов
![]() и
и
![]() равенство
равенство
![]() выполняется
при любых значениях исходных данных,
и для решения рассматриваемой краевой
задачи достаточно выполнить численное
решение только двух задач Коши:
выполняется
при любых значениях исходных данных,
и для решения рассматриваемой краевой
задачи достаточно выполнить численное
решение только двух задач Коши:
- для системы
однородных уравнений (3.4) при
начальном векторе
![]() ;
;
- для системы
неоднородных уравнений (3.1) при
начальном векторе
![]() .
.
Постоянную интегрирования
![]() в
этом случае определяем по формуле
в
этом случае определяем по формуле
|
|
|
(3.15) |
Вектор решения краевой
задачи находим затем по формуле (3.5),
учитывая, что
![]() :
:
|
|
|
(3.16) |
Изложенный метод можно применить также для расчета дисков без центрального отверстия.
По условиям симметрии
радиальное перемещение центра сплошного
диска
![]() ,
т.е. коэффициенты
,
т.е. коэффициенты
![]() ,
,
![]() ,
,
![]() в
условии (1.22) принимают значения:
в
условии (1.22) принимают значения:
![]() ,
,
![]() .
.
При расчете сплошного диска формируем начальные векторы по формулам (3.13):
![]() ,
,
![]()
и выполняем численное
решение задач Коши для системы
однородных уравнений (3.4) и системы
неоднородных уравнений (3.1) при начальных
условиях
![]() и
и
![]() соответственно.
соответственно.
При численном
интегрировании матрицу коэффициентов
![]() и
вектор
и
вектор
![]() в
точке
в
точке
![]() формируем
в соответствии с уравнениями (1.39):
формируем
в соответствии с уравнениями (1.39):
|
|
|
(3.17) |
В точках
![]() элементы
матрицы
элементы
матрицы
![]() и
вектора
и
вектора
![]() вычисляем
в соответствии с выражениями (3.2) и (3.3).
вычисляем
в соответствии с выражениями (3.2) и (3.3).
Постоянную интегрирования
![]() и
решение краевой задачи
и
решение краевой задачи
![]() для
сплошного диска находим по формулам
(3.15) и (3.16), как и для диска с центральным
отверстием.
для
сплошного диска находим по формулам
(3.15) и (3.16), как и для диска с центральным
отверстием.
Алгоритм численного решения краевой задачи для диска можно представить в более компактной форме. Введем в рассмотрение матрицы:
|
|
|
(3.18) |
|
|
|
(3.19) |
|
|
|
(3.20) |
Столбцами матрицы
![]() служат
векторы
служат
векторы
![]() и
и
![]() частных
решений задач Коши для систем (3.4)
и (3.1). Матрица
частных
решений задач Коши для систем (3.4)
и (3.1). Матрица
![]() состоит
из векторов начальных условий
состоит
из векторов начальных условий
![]() и
и
![]() .
Столбцами матрицы
.
Столбцами матрицы
![]() являются
нулевой вектор и вектор
являются
нулевой вектор и вектор
![]() ,
учитывающий массовые силы инерции и
температурную деформацию диска в
соответствии с выражениями (3.3) и
(3.17).
,
учитывающий массовые силы инерции и
температурную деформацию диска в
соответствии с выражениями (3.3) и
(3.17).
Решение краевой задачи для диска сводится к решению задачи Коши для дифференциального уравнения
|
|
|
(3.21) |
при начальном условии
![]() .
В уравнении (3.21)
.
В уравнении (3.21)
![]() -
матрица, элементы которой определяются
выражениями (3.2) и (3.17). Численное
интегрирование уравнения (3.21) выполняем
методом Рунге-Кутта:
-
матрица, элементы которой определяются
выражениями (3.2) и (3.17). Численное
интегрирование уравнения (3.21) выполняем
методом Рунге-Кутта:
|
|
|
(3.22) |
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() –
матрицы производных частных решений,
определяемые выражениями:
–
матрицы производных частных решений,
определяемые выражениями:
|
|
|
(3.23) |
В результате находим
матрицы частных решений
![]() ,
,
![]() ,
... ,
,
... ,
![]() уравнения
(3.21) в точках
уравнения
(3.21) в точках
![]() ,
,
![]() ,
… ,
,
… ,![]()
![]() интервала
интервала
![]() .
.
Постоянную интегрирования
![]() определяем
по формуле
определяем
по формуле
|
|
|
(3.24) |
где
![]() ,
,
![]() -
элементы второй строки матрицы
-
элементы второй строки матрицы
![]() (первая
цифра в скобках указывает номер строки,
вторая - номер столбца матрицы),
(первая
цифра в скобках указывает номер строки,
вторая - номер столбца матрицы),
![]() -
радиальное усилие при
-
радиальное усилие при
![]() .
.
Вектор решения краевой задачи для диска находим по формуле
|
|
|
(3.25) |
где
![]() ,
,
![]() -
соответственно первый и второй
столбцы матрицы
-
соответственно первый и второй
столбцы матрицы
![]() .
.

 матрица
переменных коэффициентов
матрица
переменных коэффициентов вектор,
учитывающий массовые силы инерции и
температурную деформации
вектор,
учитывающий массовые силы инерции и
температурную деформации





 ,
,

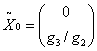





 ,
,
