Равномерная дискретизация. Теорема Котельникова

Правило выбора предельного шага при равномерной дискретизации с использованием модели сигнала с ограниченным спектром сформулировано академиком В. А. Котельниковым: «Любая непрерывная функция s(t), спектр которой ограничен частотойF_max, полностью определяется последовательностью своих значений в моменты времени, отстоящие друг от друга на интервал » Кроме того, теорема Котельникова дает и способ точного восстановления сигнала по его отсчетам.

Ряды Фурье

Для представления периодических сигналов s(t+T) = s(t) с периодом T базисные функции Yк(t) также должны быть периодическими с периодом к - целое число.

В радиотехнике в качестве базисных функций разложения Фурье используют преимущественно тригонометрические функции. Это объясняется следующими причинами:

а) функции cos wt, sin wt являются простыми, определены при всех значениях t, являются ортогональными и составляют полный набор при кратном уменьшении периода;

б) гармоническое колебание является единственной функцией времени, сохраняющей свою форму при прохождении колебания через линейную систему с постоянными параметрами, можут изменяться лишь амплитуда и фаза;

в) для гармонических функций и их комплексного анализа имеется мощный математический аппарат, найдены спектры множества форм сигналов;

г) гармоническое колебание легко осуществить на практике.

Кроме гармонического ряда Фурье применяются и другие типы разложения: по функциям Уолша, Бесселя, Хаара, полиномам Чебышева, Ляггера, Лежандра и др.

Гармонический ряд Фурье может быть представлен в следующих видах:

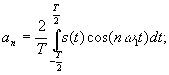
где

An  - амплитуда гармоник, nw1 - частота гармоник, jn - фаза гармоник, - комплексная амплитуда гармоник. Все виды разложения (2.3) тождественны и переходят один в другой.

При выбранном знаке перед jn  фаза гармоник является аргументом комплексной амплитуды.

Интегрирование по частям

  Из дифференциального исчисления известно, что если u и v - дифференцируемые функции от x, то

d(uv)=udv+vdu

  Отсюда

udv=d(uv)-vdu

  Интегрируя обе части этого равенства, имеем

  или

  Интегрированием по частям называется интегрирование с помощью полученной формулы.

  Основные случаи, когда применяется данный способ интегрирования:    1) подинтегральная функция содержит произведение многочлена от x на показательную функцию от x или произведение многочлена от x на sin(x) или cos(x), или произведение многочлена от x на ln(x);    2) подинтегральная функция представляет собой одну из обратных тригонометрических функций arcsin(x), arccjs(x) и т.д.;    3) подинтегральная функция есть произведение показательной функции на sin(x) или cos(x).    Пример: необходимо найти интеграл

Положим u = x, dv = sin(x)dx. Тогда du = dx, v = -cos(x). Отсюда

Дискретное преобразование Фурье (дпф)

Нам на практике надо численно, а не аналитически рассчитывать интегралы для преобразования фурье. U(t) будет поступать к нам с АЦП, как часто надо считывать с него значения и что с ними делать? Введем следующие определения.

• Полоса, частотный диапазон входного сигнала , Гц задается нами как параметр входного сигнала, диапазон [fmin,fmax]

• Мелкость разбиения полосы входного сигнала fо, Гц задается нами как параметр входного сигнала

• Число гармоник входного сигнала М определяется из fо и 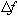. M=/fo.

• Время преобразования Тпре, сек сколько времени надо считывать из АЦП. Оно же период интегрирования Ti, определяется так же из шага, мелкости разбиения частотных спектров входного сигнала fo.

• Частота дискретизации fд, Гц с какой скоростью считывать данные U(t) из АЦП.

• Период дискретизации Тд, сек величина обратная fд

• Число отсчетов за время преобразования N показывает сколько Тд уложится за Тпре и определяется как N=Tпре/Тд

Нам надо отыскать подходящую fд для заданных условий. Опять рассмотрим сигнал вида (1). Если посмотреть на график sin, то будет видно, что выбирая значения через некоторый Тд по времени, мы непрерывную линию заменяем набором точек. Наша задача сводится к тому, чтобы найти некоторое количество точек на оси времени, при которых интеграл в преобразовании Фурье, как предел сумм, может быть для наших целей безболезненно заменен на конечную сумму из значений U(t) в этих точках.

1. Во-первых, любая гармоническая функция из ряда k*fo должна при суммировании в этих точках дать ноль;

2. во-вторых, сумма произведений этой функции на такую-же единичной амплитуды должен дать не ноль;

3. ну, и в-третьих, сумма произведений этой функции на любую единичную не равную по частоте но из ряда (2) должна дать ноль.

Тогда можно будет заменить интегрирование на суммирование.

Пусть {Un} - набор отсчетов.

Для синусоидальной составляющей с фазой 0

,

Для косинусоидальной составляющей с фазой 0

,

Для постоянной составляющей

Для гармоники m с фазой: амплитуда и фаза

,

Здесь Аm, Bm - коэффициенты Фурье, или амплитуды sin и cos составляющих с фазой ноль, m - номер детектируемой гармоники.

Можно сгруппировать вместе оценочные утверждения для ДПФ

• Чем большая точность с точки зрения различимости соседних частот в спектре входного сигнала требуется, тем меньше шаг fo и тем больше время преобразования Тпре, на котором сигнал должен быть стационарным, подходящим для преобразования.

• Подбор частоты дискретизации fд определяется в б"ольшей степени шириной полосы входного сигнала , чем абсолютным значением fmax.

• Число отсчетов N определяется соотношением Tпре и Тд.

Спектр периодического сигнала является дискретным и представляет набор гармонических колебаний, в сумме составляющий исходный сигнал. Одним из преимуществ разложения сигнала в спектр является следующее. Сигнал, проходя по цепи, претерпевает изменения (усиление, задержка, детектирование, изменение фазы, ограничение и т. д.). Токи и напряжения в цепи под действием сигнала описываются дифференциальными уравнениями, соответствующими элементам цепи и способу их соединения. Линейные цепи описываются линейными дифференциальными уравнениями, причем для линейных цепей верен принцип суперпозиции, согласно которому действие на систему сложного сигнала, состоящего из суммы простых сигналов, равно сумме действий от каждого составляющего сигнала в отдельности. Это позволяет при известной реакции системы на какой-либо простой сигнал, например, на синусоидальное колебание с определенной частотой, определить реакцию системы на любой сложный сигнал, разложив его в ряд по синусоидальным колебаниям