Информация и сигнал. Определения

Имеется множество определений понятия информации от наиболее общего философского (информация есть отражение реального мира) до практического (информация есть все сведения (данные), являющиеся объектом хранения, передачи, преобразования). Информация- совокупность сведений об объектах, рассматриваемая с позиций передачи этих сведений в пространстве и во времени.

Передается информация в виде сигналов.Сигнал- это физический процесс, распространяющийся в пространстве и времени, параметры которого способны отображать (содержать) сообщение. Сигнал может быть звуковым, световым, в виде почтового отправления и др. Наиболее распространен сигнал в электрической форме в виде зависимости напряжения от времени U(t).

Сообщение- это информация, выраженная в определенной форме и предназначенная для передачи от источника к пользователю (тексты, фото, речь, музыка, телевизионное изображение и др.). Сообщение может бытьпредставлено в виде:

• знаков (печать),

• звуковых сигналов (речь, музыка),

• светового изображения или сигнала и др.

Преобразование речи и музыки в электрический сигнал осуществляется с помощью:

• микрофона,

• преобразование изображений - с помощью телевизионных передающих трубок.

• Письменное сообщение сначала кодируется, когда каждая буква текста заменяется комбинацией стандартных символов (точки - тире, ноль - единица), которые затем преобразуются в стандартные электрические сигналы (например, импульсы разной длительности, полярности и т. д.).

Сигналы

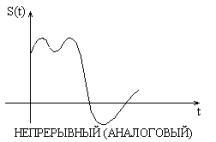
Под сигналом s(t) будем понимать изменение во времени одного из параметров физического процесса.

Классификация сигналов

Детерминированным называется сигнал, который точно определен в любой момент времени (например, задан в аналитическом виде). Детерминированные сигналы могут быть периодическими и непериодическими.

Периодическим называется сигнал, для которого выполняется условие s(t)=s(t + кT), где к - любое целое число, Т - период, являющийся конечным отрезком времени. Пример периодического сигнала - гармоническое колебание

Любой сложный периодический сигнал может быть представлен в виде суммы гармонических колебаний с частотами, кратными основной частоте

Непериодический сигнал, как правило, ограничен во времени.

Случайным сигналом называют функцию времени, значения которой заранее неизвестны и могут быть предсказаны лишь с некоторой вероятностью. В качестве основных характеристик случайных сигналов принимают:

  а) закон распределения вероятности (относительное время пребывания величины сигнала в определенном интервале);

б) спектральное распределение мощности сигнала.

Формы представления детерминированных сигналов

ЦИФРОВОЙ	Цифровой сигнал представляет из себя комбинацию узких импульсов одинаковой амплитуды, выражающих в двоичном виде дискретные отсчеты сигнала.

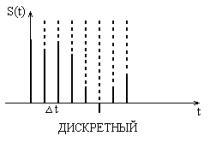
Дискретизация непрерывных сигналов

При передаче непрерывных сообщений по системам связи c использованием импульсной модуляции или кодирования возникает необходимость дискретизации сообщений по времени. В последнее время необходимость дискретизации непрерывных сигналов объясняется развитием методов квантования, дискретного анализа формы сигналов, развитием цифровой и вычислительной техники.

Сущность дискретизации заключается в том, что непрерывность во времени функции s(t)заменяется последовательностью коротких импульсов, амплитуды которых (координаты)с_кв общем случае определяются с помощью дискретных весовых функцийx_к(t) .

Воспроизведение непрерывной функции по ее дискретным координатам производится с помощью системы базисных функций Иногда весовые и базисные функции принимают одинаковыми Ввиду сложности определения координатных функций более широкое распространение получили методы дискретизации, при которых сигналs(t)заменяется совокупностью его мгновенных значений , называемых выборками, или отсчетами. Роль весовых функций в этом случае играютd-функции ,Dt - шаг дискретизации (может быть неравномерным). . Шаг дискретизации должен быть таким, чтобы было возможно восстановление непрерывной функции по ее отсчетам с допустимой точностью.