
- •Тема № 5. Алгоритмы сортировки. Сравнительный анализ
- •5.1. Введение
- •5.2. Описание алгоритмов
- •3.Пиромидальная сортировка (сортировка с помощью кучи).
- •4. Быстрая сортировка.
- •5.3. Теоретические аспекты определения времени выполнения сортировок
- •5.3.1 Алгоритм сортировки Insertion Sort
- •5.3.2. Алгоритм сортировки Quick Sort.
- •5.3.3. Алгоритм сортировки Heap Sort.
- •5.3.4. Алгоритм сортировки Merge Sort.
- •5.4. Практические аспекты сравнения
3.Пиромидальная сортировка (сортировка с помощью кучи).
Рассмотрим еще один алгоритм сортировки, а именно - пирамидальную сортировку. Время работы этого алгоритма, как и время работы алгоритма сортировки слиянием (и в отличие от времени работы алгоритма сортировки вставкой), равно O(nlgn). Как и сортировка методом вставок, и в отличие от сортировки слиянием, пирамидальная сортировка выполняется без привлечения дополнительной памяти: в любой момент времени требуется память для хранения вне массива только некоторого постоянного количества элементов. Таким образом, в пирамидальной сортировке сочетаются лучшие особенности двух рассмотренных ранее алгоритмов сортировки.
Пирамида (binaryheap)
- это структура данных, представляющая
собой объект-массив, который можно
рассматривать как почти полное бинарное
дерево (см. тему № 2). Каждый узел этого
дерева соответствует определенному
элементу массива. На всех уровнях, кроме,
может быть, последнего, дерево полностью
заполнено (заполненный уровень — это
такой, который содержит максимально
возможное количество узлов). Последний
уровень заполняется слева направо до
тех пор, пока в массиве не закончатся
элементы. Представляющий пирамиду
массивА является объектом с двумя
атрибутами:length [A],
т.е. количество элементов массива, иheap_size
[A], т.е. количество
элементов пирамиды, содержащихся в
массивеА. Другими словами, несмотря
на то, что в массивеА [1..length
[А]] все элементы могут быть корректными
числами, ни один из элементов, следующих
после элементаА[heap__size[A]],
гдеheap_size
[А]
![]() length [А], не
является элементом пирамиды. В корне
дерева находится элементА [1], а
дальше оно строится по следующему
принципу: если какому-то узлу соответствует
индексi, то индекс его
родительского узла вычисляется с
помощью представленной ниже процедурыParent(i),
индекс левого дочернего узла - с
помощью процедурыLEFT(i),
а индекс правого дочернего узла — с
помощью процедурыRight(i):
length [А], не
является элементом пирамиды. В корне
дерева находится элементА [1], а
дальше оно строится по следующему
принципу: если какому-то узлу соответствует
индексi, то индекс его
родительского узла вычисляется с
помощью представленной ниже процедурыParent(i),
индекс левого дочернего узла - с
помощью процедурыLEFT(i),
а индекс правого дочернего узла — с
помощью процедурыRight(i):
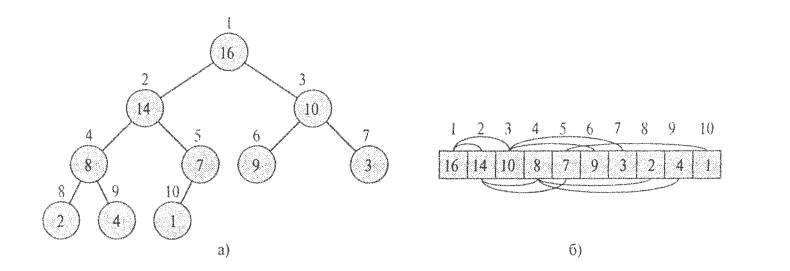
Рис. 5.3. Построение пирамиды.
Принцип работы метода.
Алгоритм основан на том, что сортируемому массиву может быть поставлено в соответствие двоичное дерево, каждый узел которого соответствует одному элементу массива с некоторым номером kи этот узел содержит ссылки на два других узла, соответствующих элементам с номерами2k+1и2k+2. Корень дерева соответствует элементу с номером0(ноль).
Дальнейшие действия следующие - массив переупорядочивается так, чтобы для любого kвыполнялись неравенства:
![]()
![]()
Затем массив еще раз переупорядочивается,
уже по возрастанию номеров. Каждый из
этих шагов требует
![]() операций.
операций.
Естественно, такой алгоритм работает быстрее и требует меньше памяти, но, наверное, он еще менее очевиден, чем рекурсивный.
Работа алгоритма пирамидальной сортировки начинается с вызова процедуры BuilD_Max__HEAP, с помощью которой из входного массиваA[1..n], где
n=length [А], создается невозрастающая пирамида. Поскольку наибольший элемент массива находится в корне, т.е. в элементеА [1], его можно поместить в окончательную позицию в отсортированном массиве, поменяв его местами с элементомА [п]. Выбросив из пирамиды узелп (путем уменьшения на единицу величиныhcap_size [А]}, мы обнаружим, что подмассивА [1.. (n- 1)] легко преобразуется в невозрастающую пирамиду. Пирамиды, дочерние по отношению к корневому узлу, после обмена элементовA[1] и А [n] и уменьшения размера массива остаются невозрастающими, однако новый корневой элемент может нарушить свойство невозрастания пирамиды. Для восстановления этого свойства достаточно вызвать процедуруМах_НеаРIFY(A,1), после чего подмассивА [1.. (n— 1)] превратится в невозрастающую пирамиду. Затем алгоритм пирамидальной сортировки повторяет описанный процесс для невозрастающих пирамид размераn-1,n-2,... ,2.
Heapsort(A)
1 Build_Max_Heap(A)
2 for i
![]() tength[A]
downto 2
tength[A]
downto 2
3 do Обменять
A[1]
![]() A[i]
A[i]
heap_size[A]
 hеар_size[A] - 1
hеар_size[A] - 1Max_Heapify(A, 1)
На рис. 5.4 показан пример пирамидальной сортировки после предварительного построения невозрастающей пирамиды. В каждой части этого рисунка изображена невозрастающая пирамида перед выполнением очередной итерации цикла forв строках 2-5. В частиа) этого рисунка показана исходная невозрастающая пирамида, полученная при помощи процедурыBU1LD_MAX_HEAP. В частяхб)-к) показаны пирамиды, получающиеся в результате вызова процедурыMAX_HEAPIFYв строке 5. В каждой из этих частей указано значение индексаi. В пирамиде содержатся только узлы, закрашенные светло-серым цветом. В части л) показан получившийся в конечном итоге массивА.
Время работы процедуры Heapsort равно О (nlgn), поскольку вызов процедурыBuild_Max_Heap требует времени0(п), а каждый изп — 1 вызовов процедурыMax_Heapify — времениО (lgn).
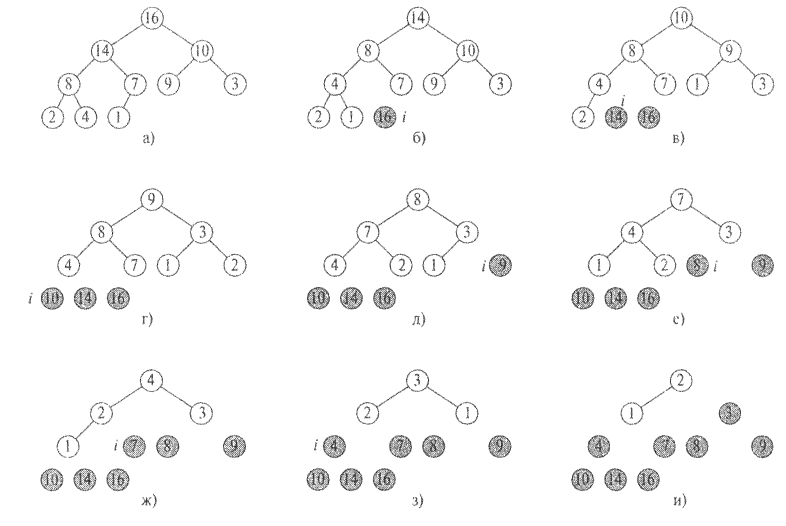

Рис. 5.4. Работа процедуры Heapsort.
Приведем псевдокоды процедур BU1LD_MAX_HEAP(создание пирамиды из неупорядоченного массива данных) иMAX_HEAPIFY(поддержка свойств пирамиды).
Max_Heapify(A,j)
l
 LEFT(i)
LEFT(i)r
 RlGHT(i)
RlGHT(i)if l
 heap_size[A] и
А[l]
> A[i]
heap_size[A] и
А[l]
> A[i]
then largest
 l
lelse largest
 i
i
6 if
r
![]() heap_size[A] и A[r] > A[largest]
heap_size[A] и A[r] > A[largest]
7 then
largest
![]() r
r
8 if
largest
![]() i
i
9 then
Обменять A[i]
![]() A[largest]
10 MaX_HeaPIFY(A,
largest)
A[largest]
10 MaX_HeaPIFY(A,
largest)
Build_Max_Heap(A)
heap_size[A]
 length[A]
length[A]for i


 downto 1
downto 1
3 do MAX_HEAPIFY(A,
i)![]()
