Тема № 7. Красно-чёрные деревья.

Червоне то любов, а чорне то журба...

( Д.Павличко)

7.1 Введение.

При рассмотрении темы № 6 было показано, что бинарные деревья поиска высоты h реализуют все базовые операции над динамическими множествами (Search, Predecessor, Successor, Minimum, Maximum, Insert и Delete) за время О (h). Таким образом, операции выполняются тем быстрее, чем меньше высота дерева. Однако в наихуд­шем случае производительность бинарного дерева поиска оказывается ничуть не лучше, чем производительность связанного списка. Красно-черные деревья пред­ставляют собой одну из множества "сбалансированных" схем деревьев поиска, ко­торые гарантируют время выполнения операций над динамическим множеством O(log₂n) даже в наихудшем случае.

Красно-черное дерево (red-black tree) - это двоичное дерево поиска, вершины которого разделены на красные (red) и черные (black). Таким образом каждая вершина хранит один дополнительный бит - её цвет.

При этом выполняются определённые требования, которые гарантируют, что глубины любых двух листьев отличаются не более чем в два раза.

Каждая вершина красно-черного дерева имеет поля color (цвет), key (ключ), left (левый ребенок), right (правый ребенок) и p (родитель). Если у вершины отсутствует ребенок или родитель, то соответствующее поле содержит NIL.

Двоичное дерево поиска называется красно-черным, если оно обладает следующими свойствами:

1. каждая вершина - либо черная, либо красная ;

2. корень дерева является черным;

3. каждый лист (NIL) - чёрный ;

4. если вершина красная, оба её ребенка чёрные ;

5. все пути, идущие вниз от корня к листьям, содержат одинаковое количество чёрных вершин

Рассмотрим произвольную вершину x красно-черного дерева и пути, ведущие вниз от неё к листьям. Все они содержат одно и то же число чёрных вершин. Число чёрных вершин в любом из них (саму вершину x не считаем) будем называть чёрной высотой (black-height) вершины x. Чёрной высотой дерева будем считать чёрную высоту его корня.

На рис. 7.1а показан пример красно-черного дерева. На рисунке черные узлы показаны темным цветом, красные — светлым. Возле каждого узла показана его "черная" высота. У всех листьев она, само собой разумеется, равна 0.

Для удобства работы с красно-черным деревом мы заменим все листья одним ограничивающим узлом, представляющим значение NIL . В красно-черном дереве Т ограничитель nil [T] пред­ставляет собой объект с теми же полями, что и обычный узел дерева. Значение color этого узла равно black (черный), а все остальные поля могут иметь произ­вольные значения. Как показано на рис. 7.1, все указатели на NIL заменяются указателем на ограничитель nil [Т].

Р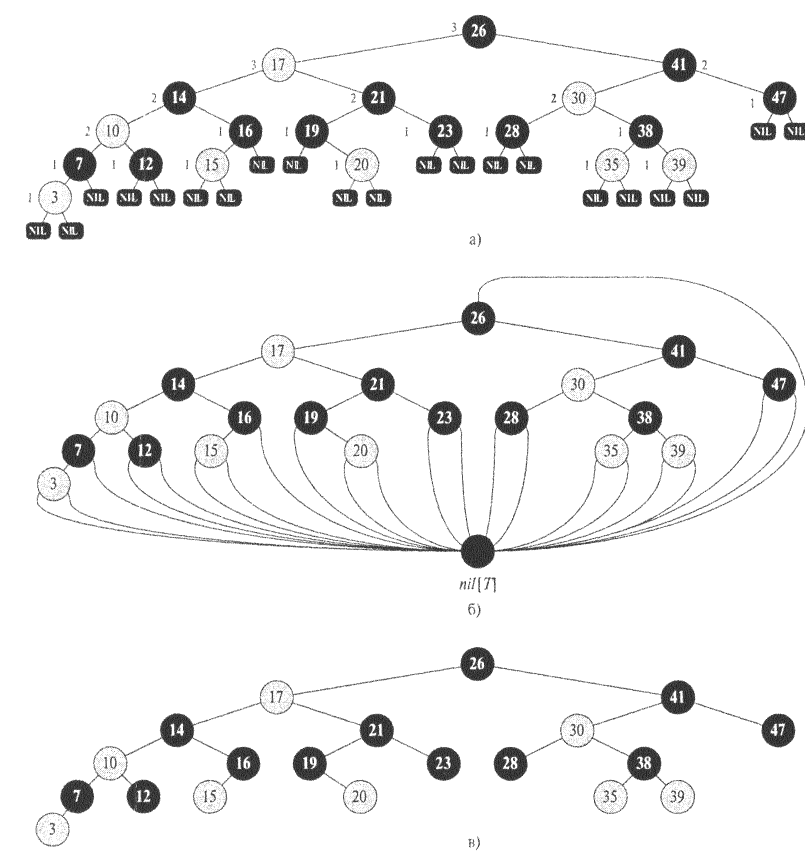ис. 7.1. Пример красно-чёрного дерева

Использование ограничителя позволяет нам рассматривать дочерний по от­ношению к узлу х nil как обычный узел, родителем которого является узел х. Хотя можно было бы использовать различные ограничители для каждого значе­ния NІL (что позволило бы точно определять их родительские узлы), этот подход привел бы к неоправданному перерасходу памяти. Вместо этого мы используем единственный ограничитель для представления всех nil — как листьев, так и роди­тельского узла корня. Величины полей р, left, right и key ограничителя не играют никакой роли, хотя для удобства мы можем присвоить им те или иные значения.

В целом мы ограничим наш интерес к красно-черным деревьям только их внутренними узлами, поскольку только они хранят значения ключей. В остав­шейся части данной темы при изображении красно-черных деревьев все листья опускаются, как это сделано на рис. 7.1в.

Количество черных узлов на пути от узла х (не считая сам узел) к листу будем называть черной высотой узла (black-height) и обозначать как bh (x). В со­ответствии со свойством красно-черных деревьев, черная высота узла — точно определяемое значение. Черной высотой дерева будем считать черную высоту его корня.

Следующая лемма показывает, почему красно-черные деревья хорошо исполь­зовать в качестве деревьев поиска.

Лемма 7.1. Красно-черное дерево с n внутренними узлами имеет высоту не более чем

2 log₂ (n + 1).