Разложение по степеням

Формула (3.5) представляет собой по существу первый, основной член разложения квантовомеханического выражения (31.3) для свободной энергии по степеням в квазиклассиче­ском случае. Представляет существенный интерес вычисление также и следующего неисчезающего члена этого разложения.

Задача о вычислении свободной энергии сводится к вычи­слению статистической суммы. Для этой цели воспользуемся тем, что последняя представляет собой след оператора (см. (3.4)); вводим обозначениедля упрощения записи громоздких выражений. Вычисление же следа оператора может производиться с помощью любой полной системы ортогональ­ных и нормированных волновых функций. В качестве таковых удобно выбрать волновые функции свободного движения систе­мы изN невзаимодействующих частиц, находящихся в некото­ром большом (но конечном) объеме V.

Эти функции имеют вид

(5.1)

где — декартовы координаты частиц, а р_i- — соответствующие им импульсы; мы нумеруем их индексом, пробегающим значе­ния i = 1,2,..., s, где s = 3N — число степеней свободы систе­мы N частиц.

Дальнейшие вычисления относятся в равной степени к си­стемам, содержащим как одинаковые, так и различные части­цы (атомы). Для того чтобы учесть в общем виде возможное различие частиц, припишем массе частицы индекс, указываю­щий номер степени свободы: (разумеется, значения трех , соответствующих одной и той же частице, во всяком случае оди­наковы) .

Наличие одинаковых частиц в теле приводит в квантовой теории к необходимости учесть так называемые обменные эф­фекты. Это значит, прежде всего, что волновые функции (5.1) должны были бы быть симметризованы или антисимметризованы по координатам частиц — смотря по тому, какой стати­стике подчиняются частицы. Оказывается, однако, что этот эф­фект приводит к появлению в свободной энергии лишь экспо­ненциально малых членов и потому не представляет никакого интереса. Кроме того, квантовомеханическая тождественность частиц сказывается на способе, которым должно производить­ся суммирование по различным значениям импульсов частиц — с этим нам придется столкнуться в дальнейшем, например при вычислении статистических сумм для квантового идеального газа. Этот эффект приводит к появлению в свободной энергии члена третьего порядка по (см. ниже) и потому тоже не ска­зывается на членах порядка, которые будут нами здесь вы­числены. Таким образом, при вычислениях мы можем вовсе не учитывать никаких обменных эффектов.

В каждой из волновых функций (5.1) импульсы имеют определенные постоянные значения. Все возможные значения каждого из образуют густой дискретный ряд (расстояния между соседними значениями обратно пропорциональны линей­ным размерам занимаемого системой объема). Поэтому сумми­рование матричных элементов по всем возможным зна­чениям импульсов можно заменить интегрированием по , учтя при этом, что число квантовых состо­яний, «приходящихся» на объем фазового пространства (все значения координат каждой частицы в объеме V и значе­ния импульсов в dp), равно.

Введем обозначение

.(5.2)

Интересующие нас матричные элементы получаются интегри­рованием по всем координатам:

.(5.3)

Искомая же статистическая сумма получится отсюда интегри­рованием еще и по импульсам.

Всего мы должны, следовательно, проинтегрировать по I фазовому пространству, точнее, по тем его областям, которые соответствуют физически различным состояниям тела, отмечаем это обстоятельство штрихом у знака интеграла:

.(5.4)

Начнем с вычисления величины I, применив для этого сле­дующий прием. Образуем производную

(оператор Н действует на все расположенные справа от него множители). Раскроем правую часть равенства, воспользовав­шись явным выражением для гамильтониана тела:

(5.5)

где— потенциальная энергия взаимодей­ствия всех частиц в теле. С помощью (5.5) получим после про­стого вычисления следующее уравнение дляI:

где

(5.6)

обычное классическое выражение для энергии тела. Это уравнение должно быть решено при очевидном условии: I = 1 при . Подстановкой

(5.7)

оно приводится к виду

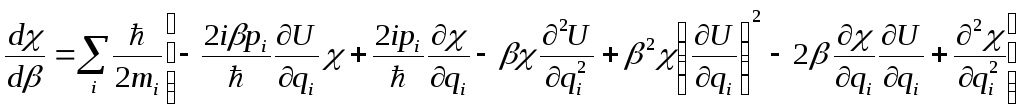(5.8)

с граничным условием при

Имея в виду получить разложение по степеням , решаем уравнение (5.8) методом последовательных приближений:

(5.9)

где приПодставляя это разложение в уравнение (5.8) и отделяя члены с различными степенями, получим уравнения

Из первого уравнения определяется, а затем из второго.

В результате простого вычисления получаем

(5.10)

Искомая статистическая сумма (5.4) равна интегралу

(5.11)

Легко видеть, что член первого порядка по в этом интегра­ле исчезает. Действительно, в этом члене подынтегральное вы­ражение есть нечетная функция импульсов квадратична по импульсам, a согласно (5.10) есть их линейная функция) и потому при интегрировании по импульсам обращается в нуль. Таким образом, переписываем (5.11) в виде

где мы ввели значение, усредненное с помощью классиче­ского распределения Гиббса:

Подставляя это выражение для статистической суммы в фор­мулу (3.3), получаем для свободной энергии

или с то же точностью

(5.12)

где— свободная энергия в классической статистике (фор­мула (3.5)).

Таким образом, следующий после классического член в раз­ложении свободной энергии оказывается второго порядка по . Это обстоятельство не случайно. В уравнение (5.8), которое мы решаем методом последовательных приближений, кванто­вав постоянная входит только в виде; поэтому и получающе­еся разложение есть разложение по степеням. В свободную же энергию, которая есть величина вещественная, могут войти только вещественные степени . Поэтому производимое здесь разложение свободной энергии (не учитывающее обменных эф­фектов) есть разложение по четным степеням .

Нам остается вычислить среднее значение . Мы видели, что в классической статистике распределения вероятно­стей для координат и импульсов независимы. Поэтому усредне­ния по импульсам и по координатам можно производить раз­дельно.

Среднее значение произведения двух различных импульсов равно, очевидно, нулю. Среднее же значение квадрата рав­но. Поэтому можно написать:

где при ипри. Осуществив с помощью этой формулы усреднение по импульсам, получим

(5.13)

Оба члена здесь могут быть объединены в один, так как входя­щие сюда средние значения связаны соотношением

(5.14)

В справедливости этого равенства легко убедиться, замечая, что

Первый член в правой стороне даст выражение, представляющее собой поверхностный эффект; ввиду макроскопичности тела им можно полностью пренебречь по сравнению со вторым членом, дающим объемный эффект.

Подставив полученное таким образом выражение для в формулу (5.12) и заменив на , найдем окончательно для свободной энергии

(5.15)

Мы видим, что поправка к классическому значению оказывает­ся величиной всегда положительной, определяющейся средними квадратами действующих на частицы сил. Эта поправка убыва­ет с увеличением массы частиц и с возрастанием температуры. Согласно сказанному выше следующий член производимо­го здесь разложения был бы четвертого порядка. Это обсто­ятельство дает возможность совершенно независимым образом вычислить член порядка, возникающий в свободной энергии благодаря особенностям суммирования по импульсам, связан­ным с квантовомеханической тождественностью частиц. Этот член формально совпадает с поправочным членом, возникаю­щим при аналогичном вычислении для идеального газа, и опре­деляется формулой:

(5.16)

(для тела, состоящего из N одинаковых частиц). Верхний знак относится к статистике Ферми, а нижний — к статистике Бозе; есть полная кратность вырождения по направлениям моментов— как электронного, так и ядерного.

Полученные формулы позволяют также получить поправоч­ные члены в функциях распределения вероятностей координат и импульсов атомов тела. Распределение вероятностей импульсов получается интегрированием по:

Член всодержит полную производную по коорди­натам и при интегрировании по ним дает величину, которая представляет собой поверхностный эффект и может быть опу­щена. Таким образом, имеем

Третий и четвертый члены в выражении (5.10) для в ре­зультате интегрирования по координатам дадут малую посто­янную (не содержащую импульсов) величину, которой в том же приближении можно пренебречь. Вынося также в постоянный коэффициент множитель , получим

Входящие сюда средние значения связаны соотношениями

(аналогичными (5.14)). Поэтому имеем

.(5.17)

Это выражение удобно переписать окончательно в следующем виде:

(5.18)

заменив с той же точностью квадратные скобки в (5.17) соот­ветствующим экспоненциальным выражением.

Таким образом, мы видим, что поправка к классической функции распределения для импульсов сводится к тому, что в экспоненте к кинетической энергии прибавляется квадратич­ное по импульсам выражение с коэффициентами, зависящими от закона взаимодействия частиц в теле.

Если мы хотим найти распределение вероятностей для како­го-либо одного из импульсов, надо проинтегрировать (5.17) по всем остальным импульсам. При этом все члены с квадра­тами,, дадут такие постоянные величины, которыми можно пренебречь по сравнению с 1, а члены с произведениями различных импульсов вообще обратятся в нуль. В результате найдем, снова переходя к экспоненциальному виду,

Мы видим, что получается распределение, отличающееся от максвелловского лишь заменой истинной температуры Т на не­которую более высокую “эффективную температуру”:

Аналогичным путем можно вычислить исправленную функ­цию распределения для координат. Она получается интегриро­ванием по импульсам:

Те же вычисления, с помощью которых было получено выраже­ние (5.13), приведут к следующему результату:

Распределение Гиббса для вращающихся тел

Выясним теперь, каким образом должно быть сформулировано для вращающихся тел распределение Гиббса; этим будет полностью исчерпан вопрос об их статистических свойствах. Что касается равномерного поступательного движения, то в силу принципа относительно­сти Галилея оно, как уже указывалось, влияет на ста­тистические свойства лишь тривиальным образом и потому не нуждается в особом рассмотрении.

В системе координат, вращающейся вместе с телом, справед­ливо обычное распределение Гиббса; в классической статистике

(6.1)

где энергия тела в этой системе как функция коорди­нат и импульсов его частиц,a F' — свободная энергия в этой же системе (отнюдь не совпадающая, однако, со свободной энер­гией покоящегося тела!). Энергия связана с энергиейв неподвижной системе соотношением

(6.2)

где — угловая скорость вращения, амомент импуль­са тела . Подставляя (6.2) в (6.1), найдем распреде­ление Гиббса для вращающегося тела в виде

(6.3)

В классической статистике распределение Гиббса для вра­щающегося тела можно представить и в другом виде. Для это­го воспользуемся следующим выражением для энергии тела во вращающейся системе координат:

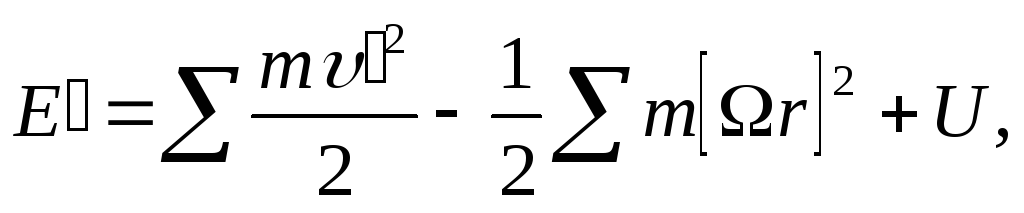(6.4)

где — скорости частиц относительно вращающейся системы, а— их радиусы-векторы. Обозначив посредством

(6.5)

не зависящую от часть энергии, получим распределение Гибб­са в виде

Функция определяет вероятность, отнесенную к элементу фазового пространствагдеимпульсы частиц тела. Поскольку при нахождении дифференциалов импульсов координаты долж­ны считаться постоянными, то, и мы можем напи­сать распределение вероятностей, выраженное через координа­ты и скорости частиц:

(6.6)

где посредством С мы обозначили для краткости множитель вместе с произведением масс частиц, возникающим при переходе от дифференциалов импульсов к дифференциалам ско­ростей.

Для неподвижного тела мы имели бы

(6.7)

с тем же самым выражением (6.5) для— теперь как функции от скоростей в неподвижной системе координат. Та­ким образом, мы видим, что распределение Гиббса по коорди­натам и скоростям для вращающегося тела отличается от рас­пределения для неподвижного тела только дополнительной по­тенциальной энергией, равной

Другими словами, для статистических свойств тела вращение оказывается эквивалентным появлению некоторого внешнего поля, соответствующего центробежным силам. Кориолисовы же силы не влияют на эти свойства.

Необходимо, однако, подчеркнуть, что последний результат относится только к классической статистике. В квантовом слу­чае для вращающегося тела справедливо выражение

(6.8)

для статистического оператора, аналогичное выражению (6.3). Формально можно привести этот оператор к виду, соответству­ющему (6.6), причем скорости заменятся операторамиОднако компоненты этого векторного оператора уже не будут коммутировать друг с другом, как это имеет место для оператораскорости в неподвижной системе; поэтому ста­тистические операторы, соответствующие выражениям (6.6) и (6,7), будут, вообще говоря, существенно отличаться друг от друга, даже помимо присутствия в одном из них центробежной энергии.