Распределение Максвелла

Энергия в формуле распределения Гиббса классиче­ской статистики всегда может быть представлена как сумма двух частей — кинетической и потенциальной энергий. Из них первая есть квадратичная функция от импульсов атомов, а вторая—функция от их координат, причем вид этой функ­ции зависит от закона взаимодействия частиц внутри тела (и от внешнего поля, если такое имеется). Если кинетическую и потенциальную энергии обозначить соответственно как и, то и вероятность напишется в виде

т. е. разбивается на произведение двух множителей, из которых один зависит только от координат, а другой — только от им­пульсов. Это означает, что вероятности для импульсов и коор­динат независимы друг от друга в том смысле, что определен­ные значения импульсов никак не влияют на вероятности тех или иных значений координат, и обратно. Таким образом, веро­ятность различных значений импульсов может быть написана в виде

а распределение вероятности для координат

Так как сумма вероятностей всех возможных значений им­пульсов (и то же самое для координат) должна быть равна еди­нице, то каждая из вероятностей идолжна быть нор­мирована, т.е. их интегралы по всем возможным для данного тела значениям импульсов или координат должны быть равны единице. Из этих условий можно определить постоянныеив (29.1) и (29.2).

Займемся изучением распределения вероятностей для им­пульсов, еще раз подчеркнув при этом весьма существенный факт, что в классической статистике такое распределение нис­колько не зависит от рода взаимодействия частиц внутри систе­мы или от рода внешнего поля и потому распределение может быть выражено в виде, пригодном для любых тел¹).

Кинетическая энергия всего тела равна сумме кинетических энергий каждого из входящих в него атомов, и вероятность опять разбивается на произведение множителей, из которых каждый зависит от импульсов только одного из атомов. Это вновь означает, что вероятности импульсов различных атомов не зависят друг от друга, т.е. импульс одного из них никак не влияет на вероятности импульсов всех других. Поэтому можно писать распределение вероятностей для импульсов каждого атома в отдельности.

Для атома с массой кинетическая энергия равнагдедекартовы составляющие его импульса, а распределение вероятностей имеет вид

Постоянная определяется условием нормировки. Интегриро­вания поразделяются и производятся с помощью известной формулы

В результате находим, и мы получаем оконча­тельное распределение вероятностей для импульсов в виде

Переходя от импульсов к скоростям , можно написать аналогичное распределение для скоростей:

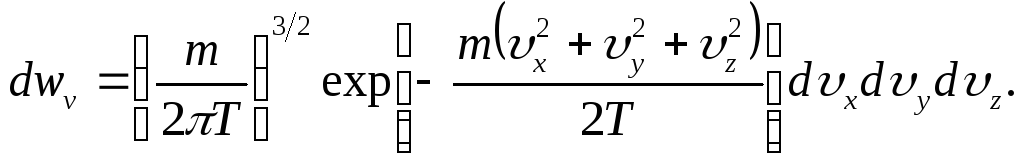(1.4)

Это — так называемое распределение Максвелл .Заметим, что оно снова распадается на произведение трех независимых множителей:

каждый из которых определяет распределение вероятностей для отдельной компоненты скорости.

Если тело состоит из молекул (например, многоатомный газ), то наряду с распределением Максвелла для отдельных ато­мов такое же распределение имеет место и для поступательного движения молекул как целых. Действительно, из кинетической энергии молекулы можно выделить в виде слагаемого энергию поступательного движения, в результате чего искомое распре­деление выделится в виде выражения (1.4), в котором под надо будет понимать полную массу молекулы, а подкомпоненты скорости ее центра инерции. Подчеркнем, что рас­пределение Максвелла для поступательного движения молекул может иметь место вне зависимости от характера внутримо­лекулярного движения атомов (и вращения молекулы), в том числе и в случае, когда последнее должно описываться кванто­вым образом.

Выражение (1.4) написано в декартовых координатах в “пространстве скоростей”. Если от декартовых координат пе­рейти к сферическим, то получится

где абсолютная величина скорости, аиполярный угол и азимут, определяющие направление скорости. Интегрируя по углам, найдем распределение вероятностей для абсолютной ве­личины скорости

Иногда бывает удобно пользоваться цилиндрическими коор­динатами в пространстве скоростей. Тогда

где компонента скорости по осиперпендикулярная к осикомпонента скорости, аугол, определяющий напра­вление последней.

Вычислим среднее значение кинетической энергии атома. Согласно определению средних значений, на­ходим для любой декартовой компоненты скорости

Поэтому среднее значение кинетической энергии атома равно. Можно, следовательно, сказать, что средняя кинетическая энергия всех частиц тела в классической статистике всегда рав­на, гдеN — полное число частиц.