
|
3)Постулаты квантовой механики 1)Каждой системе (состоянию кв.-мех. системы может быть поставлена в соответствие волновая функция динамических переменных, из полного набора, и времени, полностью описывающей состояние системы.
Динамические
переменные одновременно измеряемы.
В классической механике задание 2n динамических переменных полностью определяет состояние системы через функцию Гамильтона.
В
квантово-механической системе
описывается эволюция системы через
2)Каждой
физической величине ставится во
взаимооднозначное соответствие
оператор:
3)
Если собственные значения образуют дискретное множество, то говорят о дискретном спектре.
Если
собственные значения образуют
непрерывное множество, то спектр
непрерывный. 4) здесь введено понятие скалярного произведения для функций из гильбертова пространства. Гильбертово пространство – это пространство квадратично интегрируемых функций (нормируемых функций).
Это
определение для
Это аналог длины в векторном пространстве. |
7)Операторы в квантовой механике В силу принципа суперпозиции в квантовой механике используются линейные операторы. Линейный
оператор – это такой оператор
здесь
действует на произвольную функцию
Линейность:
Если
т.к.
Сопряженный оператор – это оператор, который связан с данным оператором соотношением:
Отсюда
Если
Транспонированный оператор
Отметим следующие свойства: 1)
Из выражения (4) получаем
2)
3)
Сумма
операторов:
Произведение
операторов:
В
общем случае
Коммутатор
Если
Если
Так как физические величины вещественны, то число операторов в квантовой механике сужается. Сужение класса операторов – эрмитовость операторов. Запишем определение среднего:
Так
как результаты измерений вещественны,
то
тогда
т.е.
Обозначим
Тогда из (5) получаем
Из
(6) имеем для любых
где
|
14)Коммутативность операторов и одновременная измеримость физических величин Коммутатор:
Разложение
Если
подействовать на
=
Обратное: Если коммутатор обращается в ноль, то физические величины одновременно измеримы. Пусть
Тогда
получим
Пусть
эта константа
Получили,
что функция
Это
можно было показать для любой собственной
функции оператора
Тогда
из коммутативности операторов
Величины
Полный
набор динамических переменных полностью
задает состояние системы. Но операторы
|
|
28)
Оператор перестановки и его свойства
Введем
обозначение
С учетом (**):
Получаем
частицы с симметричными и антисимметричными
волновыми функциями: бозоны и фермионы.
Кроме того, оператор
Аналогично
Это антисимметричная функция. Свойства симметричности и антисимметричности называются интегралами движения, т. е. сохраняются. Ансамбль не может переходить из одного состояния в другое (т. е. из симметричного в антисимметричное и наоборот). Симметричные функции описывают состояние систем с целым спином, т. е. ансамбль бозонов. Антисимметричные функции – ансамбль фермионов. Пусть
где
Мы будем рассматривать стационарные состояния, т. е.
где
Мы имеем
Если
всего N
частиц, то можно осуществить N!
перестановок,
тогда имеем N!
возможных функций
Так
как все
|
16)Волновое уравнение - уравнение функции, которое описывает состояние квантово-механической системы. Оно было получено Шредингером интуитивным путем и не выводится. Норма
волновой функции:
где
Получили волновое уравнение:
Каждой системе ставится в соответствие Гамильтониан, решаем с гамильтонианом уравнение Шредингера и получаем волновую функцию которая определяет эволюцию системы.
|
20)Свободная материальная точка
Для
свободной материальной точки
Это трехмерная задача
Оператор Лапласа
Оператор представим в виде суммы трех независимых операторов, которые коммутируют. В этом случае можно разделить переменные.
Тогда стационарное уравнение Шредингера запишется в виде
где
Для
Обозначим
Тогда
Решение этого уравнения
Так как частица свободная, то импульс этой частицы сохраняется. Значит сохраняется направление движения частицы.
Мы
выбираем движение частицы по направлению
оси x.
Тогда в силу сохранения импульса имеем
Для трехмерного случая
Полная волновая функция
Рассмотрим теперь коммутатор
Так
как импульс коммутирует с
1) 2)Собственная функция оператора импульса является решением волнового уравнения.
Найдем собственные значения оператора импульса.
=
Тогда
собственное значение оператора
Это первое дебройлевское соотношение.
Из
(***) вводится
Используем, что
Уравнение (***) удовлетворяет собственной функции оператора импульса. |
|
|
24. Неравенство Гайзенберга. Канонически сопряженные величины одновременно неизмеримы – это принцип неопределенности. Под
канонически сопряженными понимаем
величины
В
квантовой механике для операторов
Более
того
Это
можно записать в виде
Если
Обозначим
Тогда
из
Введем обозначение
Подставим это в неравенство Коши-Шварца, тогда
Используем эрмитовость операторов
тогда
Используем определение среднего
тогда
Или
Операторы
Первое
слагаемое обозначим Второе
слагаемое Оператор
Тогда
где
Окончательно
В полученном неравенстве математически заложен принцип неопределенности Гайзенберга.
Если
величина измерена точно, то
Если
Когда
измеряем величину
|
|

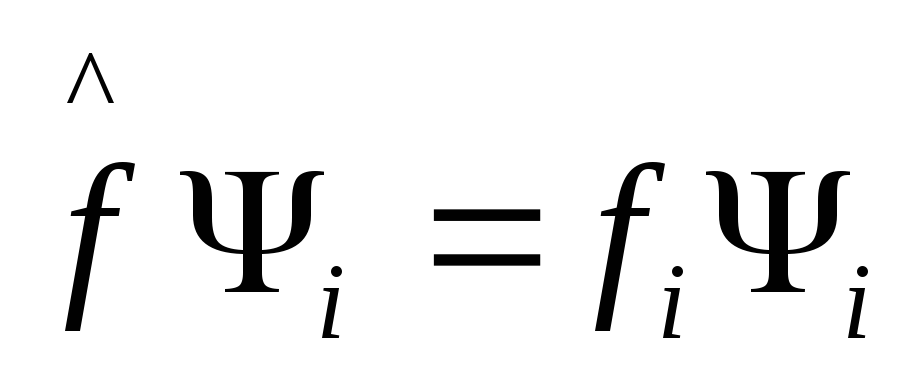 ,
,
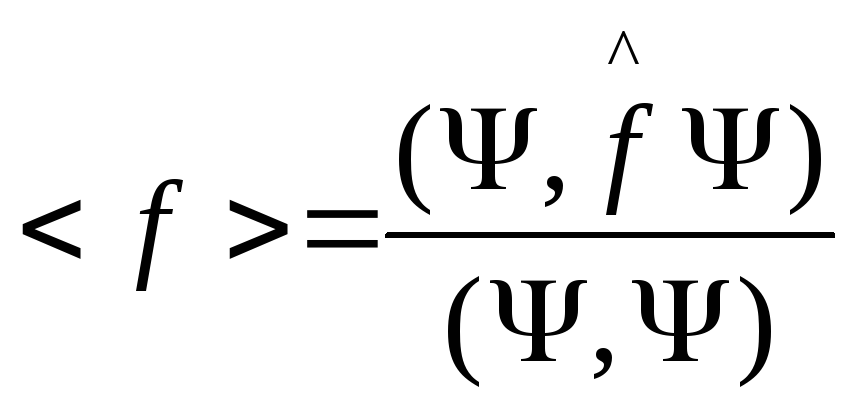
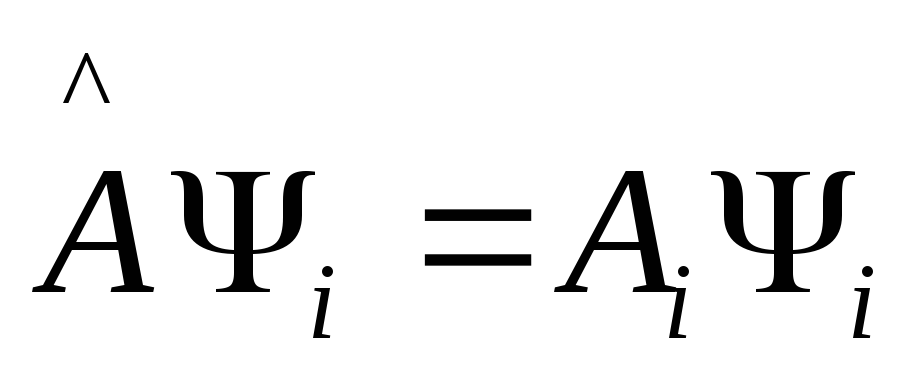 (1)
(1) (3)
(3)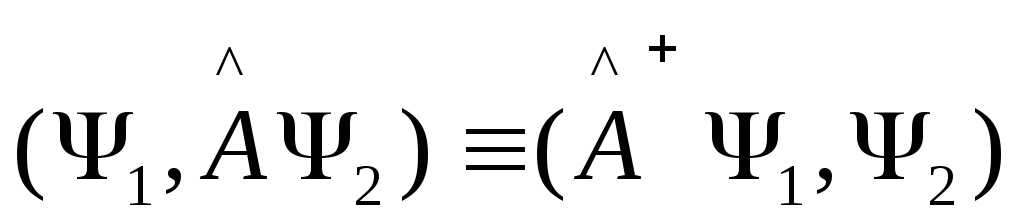

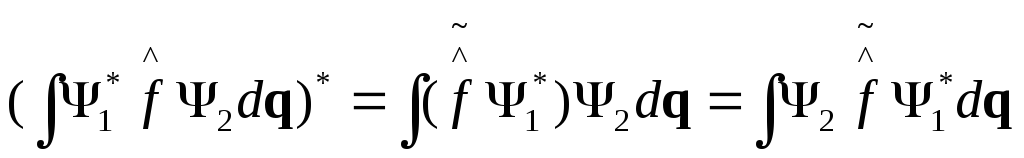
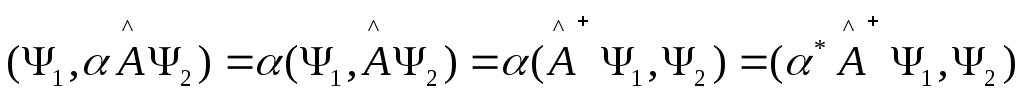 (4)
(4)

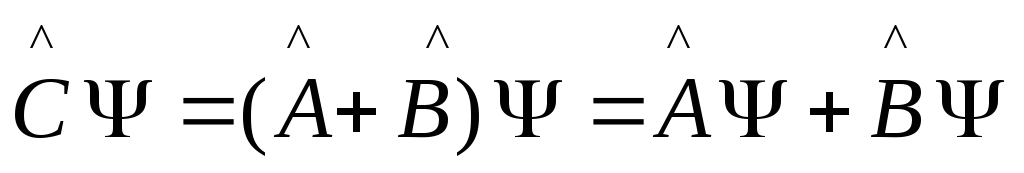
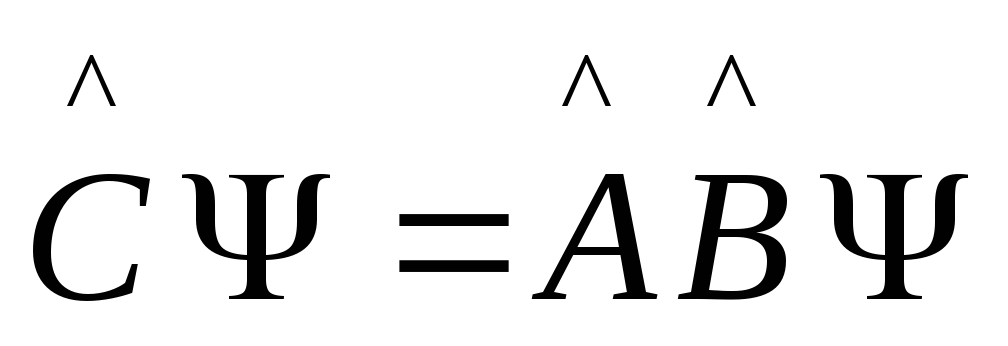 .
Это операторное равенство предполагает
.
Это операторное равенство предполагает
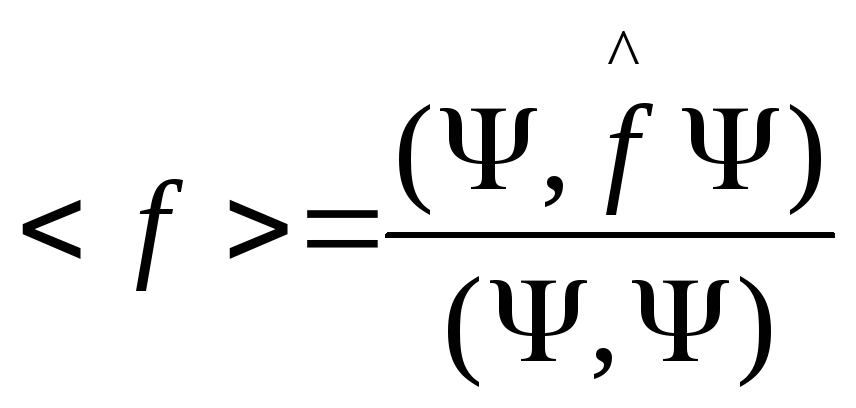
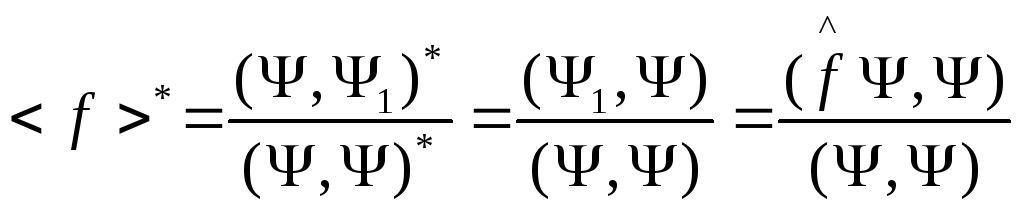
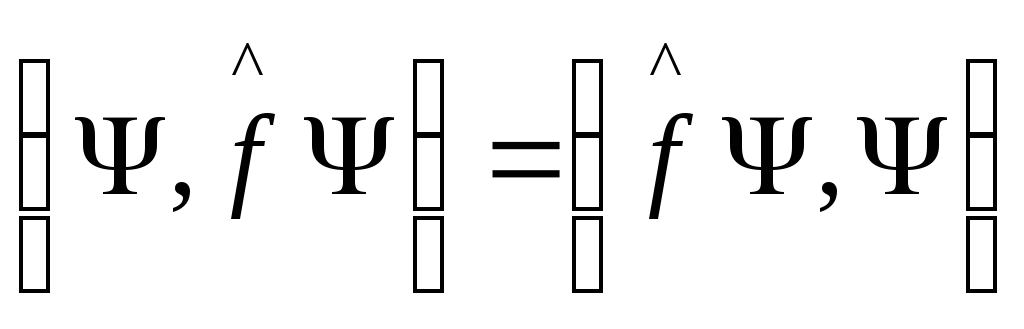 (6)
(6)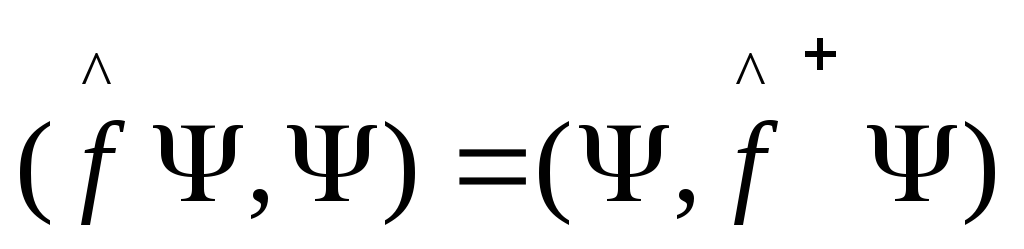 ,
,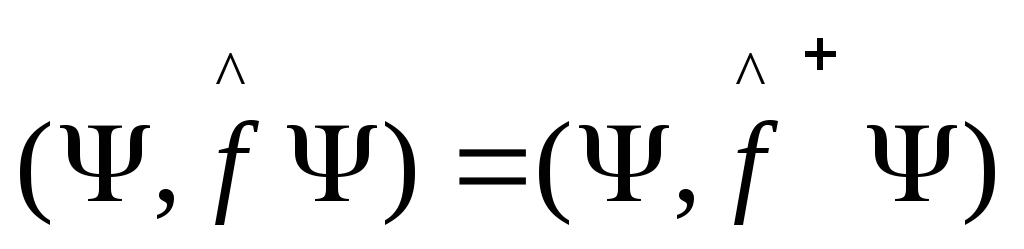 ,
,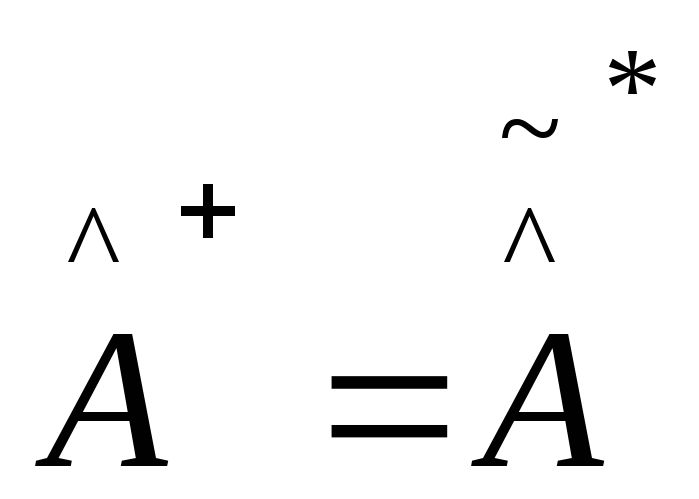 (сопряженный
и транспонированный)
(сопряженный
и транспонированный)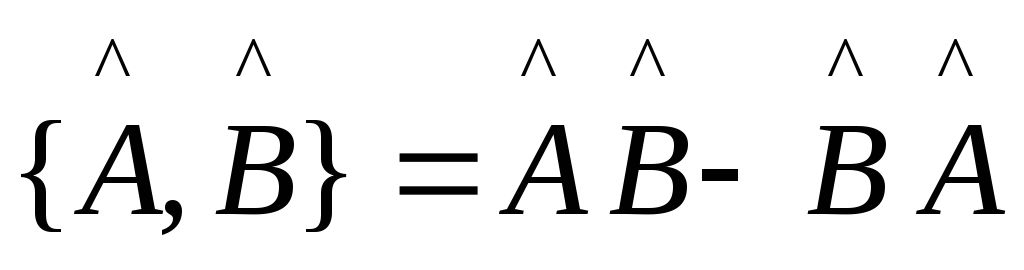 .
Если существует
.
Если существует


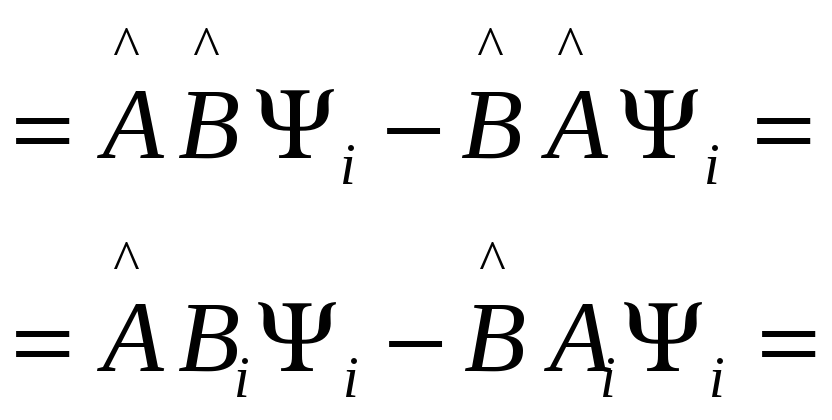
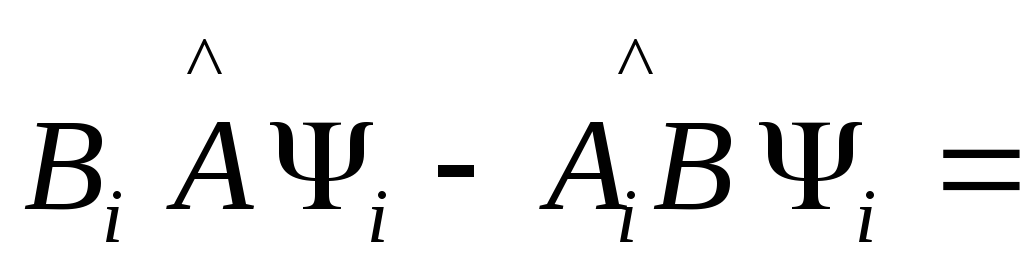
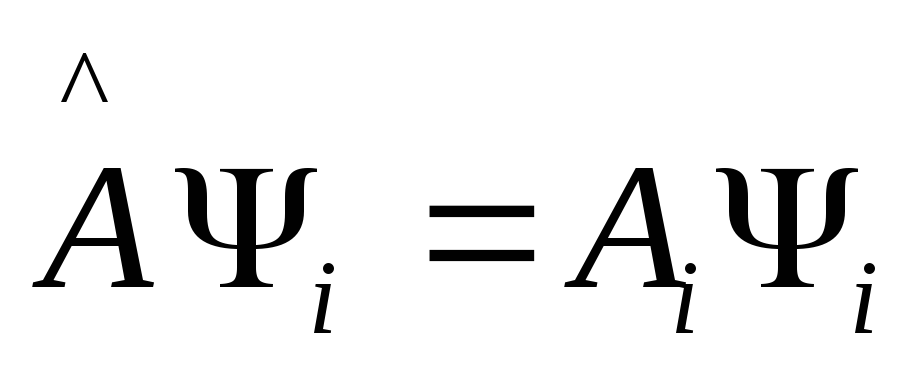 .
Подставляем ее в коммутатор
.
Подставляем ее в коммутатор
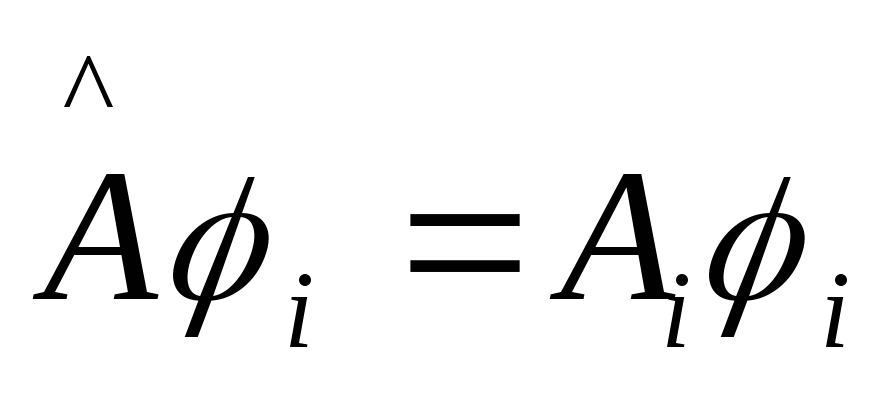 .
Мы рассматриваем невырожденный спектр.
Это значит, что существует однозначное
соответствие одно собственного
значения и одной собственной функции.
Разница между функциями
.
Мы рассматриваем невырожденный спектр.
Это значит, что существует однозначное
соответствие одно собственного
значения и одной собственной функции.
Разница между функциями
 ,
тогда
,
тогда
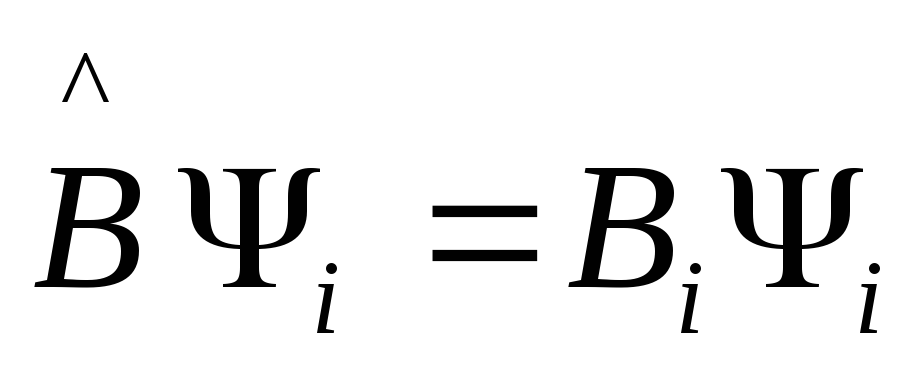 .
.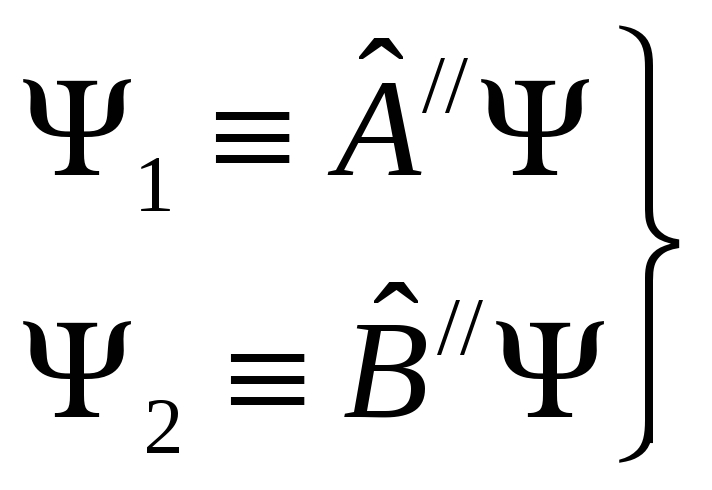
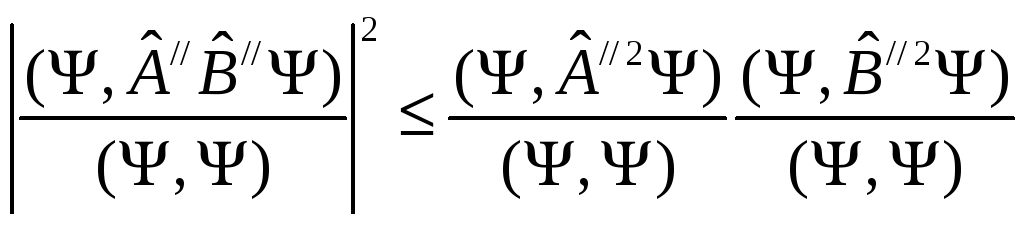
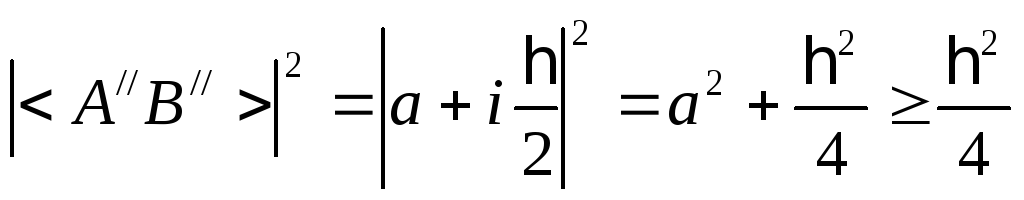 .
.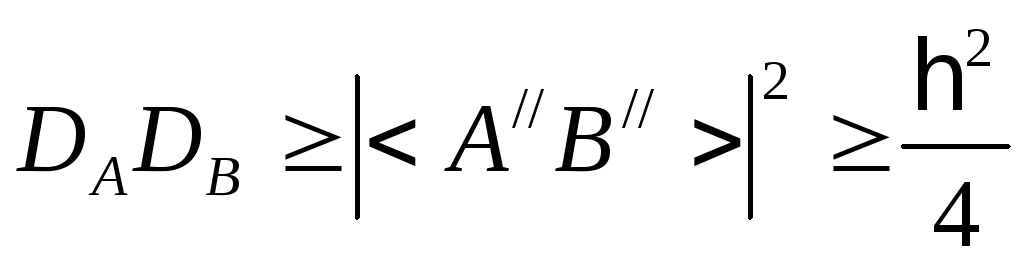 .
.