
|
1)Классическое и квантовое описание системы. Имеется источник частиц, экран с достаточно узким отверстием. Картину наблюдаем на Э2
1) При классическом описании опыт 3 давал бы сложение интенсивностей от опыта 1 и 2. Однако опыт 3 показал интерференционную картину, а это волновые свойства. Частица с определенной вероятностью проходит как через щель 1 так и через щель 2. Нельзя точно сказать через какую щель пройдет электрон. Классическая интерпретация (с числом степеней свободы n=1) решается составлением уравнений в форме Гамильтона:
Можно найти траекторию частицы. В общем случае состояние механической системы определяется 2n динамическими переменными. Т. е. 2n начальных условий.Но опыт показал, что мы не можем определить траекторию частицы в микромире.Количество динамических переменных, которые могут быть одновременно измерены в микромире, в квантовой механике – n.
Скорость
Координата
|
2)Принцип неопределенности.
Две формулировки: 1)В микромире понятие “траектория” отсутствует 2)Канонически сопряженные величины одновременно неизмеримы В трехмерном пространстве канонически сопряженные величины будут: px и x py и y pz и z Здесь n=3. Имеем 3 одновременно измеряемые динамические переменные. Например:
x, y, pz и тд. |
5)Волновая функция и ее свойства.Волновая функция динамических переменных и времени определяет состояние системы точностью до фазового множителя. Т. е.
|
|
4)Полный набор динамических переменных Полный набор динамических переменных – это наибольший набор независимых одновременно измеряемых динамических переменных. Измерение полного набора динамических переменных полностью определяет состояние квантово-механической системы. Число динамических переменных в квантовой системе - n и по сравнению с классической системой (2n) уменьшается в 2 раза. Максимальный набор – это значит, что к этому набору не может быть добавлена ни одна другая переменная, которая не являлась бы их функцией. В этом случае они не зависимы. Каждая из этих переменных не является функцией другой переменной из этого же набора. Зависимость не, а функциональная. |
||
|
8)Понятие о теории представлений Представление – это совокупность переменных в которых решается задача, т. е. набор динамических переменных. Рассмотрим одну материальную точку. Число степеней свободы n=3. Здесь могут быть 2 случая:
Под
Под
Операторы
в
Оператор
координаты
Оператор
импульса
Здесь
Операторы
в
Оператор
координаты
Оператор
импульса
Здесь
|
||
|
6)Принцип
суперпозиции состоянийЕсли
мы имеем состояние системы, описываемое
функцией
Иначе:
если
Отсюда
получаем: уравнения, которым подчиняется
Этот же вывод распространяется и на операторы и на операторы в квантовой механике. Принцип суперпозиции требует использования в квантовой механике линейных операторов. |
||
|
12)Среднее значение измеряемой величины. По определению
Рассмотрим
оператор
По
равенству Парсеваля
(3) Подставляя (3) в числитель, а (2) в знаменатель для (1), тогда имеем
Из
теории вероятности
|
13)Вероятность результатов измерения
Если
система находится в состоянии
В
общем случае
Условие
при котором собственная функция
оператора
Если
полная производная оператора
Для
непрерывного спектра, вероятность
того, что результаты измерения величины
A
для системы, находящейся в состоянии
или
плотность вероятности
|
15)Операторы
координаты
Будем
использовать координатное представление
(
Действие
Здесь строго соблюдается последовательность операторов при раскрытии векторного произведения, например, первая компонента:
однако для частного случая декартовых координат порядок операторов не существенен.
Оператор
энергии или Гамильтониан
здесь
Для одной материальной точки гамильтониан имеет вид:
Координата t – признак внешнего нестационарного поля.
Для
одной материальной точки:
|
|
21)Производная оператора по времени
Пусть
средняя от величины
Ставим
в соответствие величине
Распишем:
В
классической механике
В
квантовой механике существует связь:
В
пределе
В квантовой механике большинство операторов явно не зависят от времени и их частные производные равны 0.
|
22)Интегралы движения в кв. механике.
В
классической механике
В
квантовой механике, чтобы величина
Для
того чтобы физическая величина
сохранялась, необходимо и достаточно,
чтобы
1)т.
к.
2)
3)
4)
|
17)Оператор Гамильтона различных систем. Этот вопрос идентичен рассмотренной в классической механике будут те же соотношения, но для операторов
Поставим
в соответствие конкретной системе
операторы
В
декартовой системе координат Здесь n – число точек в системе.
Мы
рассматриваем
Мы
рассматриваем декартову систему
координат. Гамильтониан
Здесь
Индекс
a
означает,
что разные частицы могут взаимодействовать
с внешним полем по разному закону.
Если все частицы одинаковые и одинаково
взаимодействуют с внешним полем, то
индекс a
убирается.Внутреннее
взаимодействие
Центральное
поле
Рассмотрим систему двух материальных точек. Мы рассматриваем частный случай – замкнутая система двух материальных точек.
В
случае классической механики:
Отсутствие t в энергии взаимодействия – это однородность времени и закон сохранения энергии.
Зависимость
энергии от модуля
В
квантовой механике в
где
|
|
19)Стационарное состояние различных систем
Задача
Штурма-Лиувилля для оператора
Волновое
уравнение:
Как
только поставили в соответствие
системе оператор
Собственные функции задачи Штурма-Лиувилля и функции, являющиеся решением волнового уравнения совпадают при условии выполнения:
Так
как
Рассмотрим
стационарную задачу
Использую (*) и (**), получим
Это дифференциальное уравнение имеет решение
Подставим эту функцию в (*), тогда
Тогда получим
Получили стационарное уравнение Шредингера.
|
11)Решения задачи на собственные значения в случае операторов с дискретным спектром.
Как
частные случай рассмотрим
Для
эрмитова оператора
Рассмотрим
теперь
Умножая
(1) скалярно на
Теперь
(2) умножаем справа на
Почленно из (3) – (4):
|
10)Решения задачи на собственные значения в случае операторов с непрерывным спектром.
Используем искусственную операцию – введем понятие собственных дифференциалов, по определению:
т.
е. на числовой оси рассмотрим функции
с равным весом на интервале
Условие
ортонормируемости:
Здесь
уже
Собственные
функции
|
|
23)Флуктуации физических величин.
Пусть
есть
Мы вводили флуктуацию
Перенесем
все это на язык квантовой механики,
т. к. физической величине
Можно
показать, что
Теперь
если обозначить
|
25)Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: второе приближения. Для членов второго порядка малости из
запишем
Рассмотрим
теперь (10*): его можно в общем случае
записать, учмтывая, что
Re=
Случай
Обычно пишут
|
26)Спин: теория и эксперимент. Рассмотрим Na. У него есть желтая линия . Возникает при переходе с уровня 3p на 3s.
Первоначально
ее длина была 5892
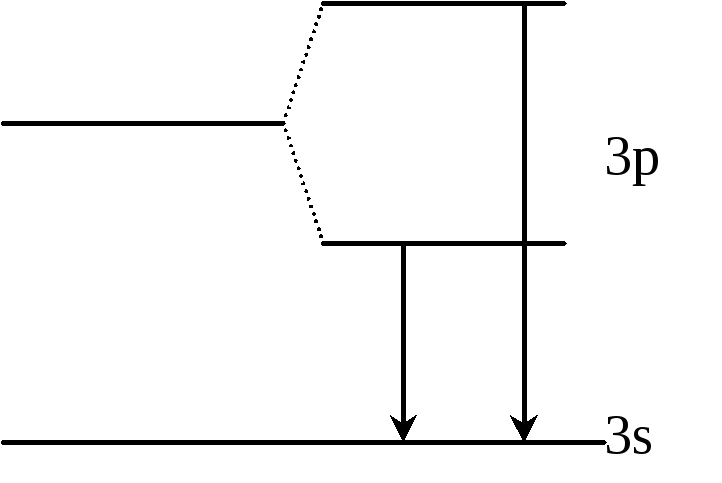
Было обнаружено, что эта линия расщепляется на две: дублет. Возникла идея расщепления уровня 3p на два, тогда можно объяснить возникновение двух линий.
Их
длины: 5896
В 1925 г. Была предложена гипотеза спина, т. е. собственного механического момента. У электрона спиновое число s=0.5. Впоследствии Паули ввел спин в теорию.
Если
имеем одну частицу, то она характеризуется
орбитальным квантовым числом
Состовная
частица (атом) состоит из многих
микрочастиц. Можно рассматривать эту
составную частицу вцелом и приписать
ей момент
Энергетический
уровень этой составной частицы в
некоторых полях будет зависеть от
орбитальных моментов микрочастиц Эти моменты являются внутренним свойством этой составной частицы. Можно рассматривать 2 момента:
1) 2)Частица сама движется по некоторой траектории.
У
частицы есть еще квантовое число
Вводят оператор собственного механического момента:
По аналогии
Спин – внутреннее свойство частицы. Его смысл – у частицы есть внутренний параметр, который реагирует на вращение координат независимо от места положения частицы. |
|
27)Спиновая переменная волновой функции
Рассмотрим
одну частицу – система с 3 степенями
свободы. Задача решается в
Вероятность
обнаружения частицы
Если
хотим найти реализацию конкретного
значения
Рассмотрим действие операторов в пространстве четырех переменных Было известно
и интеграл (**) переходит в интеграл:
|
29)Принцип тождественности.
Этот принцип в квантовой механике определенным образом связан с принципом Гайзенберга. Если рассмотрим ансамбль одинаковых частиц, то идентификация этих частиц невозможна. Одинаковые частицы обладают всеми одинаковыми внутренними свойствами (m, e, s, …). Мы не можем в квантовой механике ввести траекторию, тогда не можем различить одинаковые частицы. Например, в электронном газе не отдельные частицы, а целый ансамбль. В такой системе – тождественные частицы. В ансамбле одинаковых частиц реализуются состояния, инвариантные относительно их перестановок. Т. к. частицы идентифицировать невозможно, то мы не можем различить состояния, которые вызваны перестановкой частиц. |
32) Фермионы и бозоны
Все
проводится по аналогии с
Так
как
Но
Собственные значения оператора:
Тогда здесь всего 2s+1 значение оператора.
Перейлем
к классическому пределу:
Ввиду
связи
Ясно,
что так как
В классической механике этим величинам аналога нет и они обращаются в нуль.
В
случае спина мы не можем наложить
условие
Если
Если
Отсюда деление на 2 типа частиц: 1)Фермионы – спин полуцелый 2)Бозоны – спин целый. |

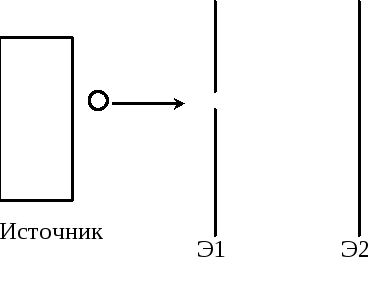 2)
2)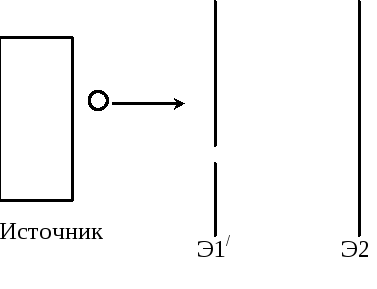 3)
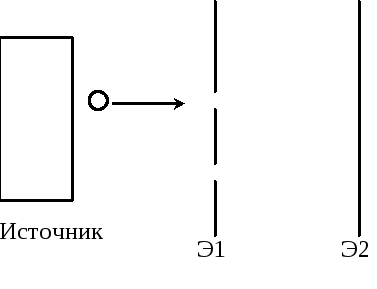
3)
 в
силу линейности опе-ра заносим его
под знак суммы
в
силу линейности опе-ра заносим его
под знак суммы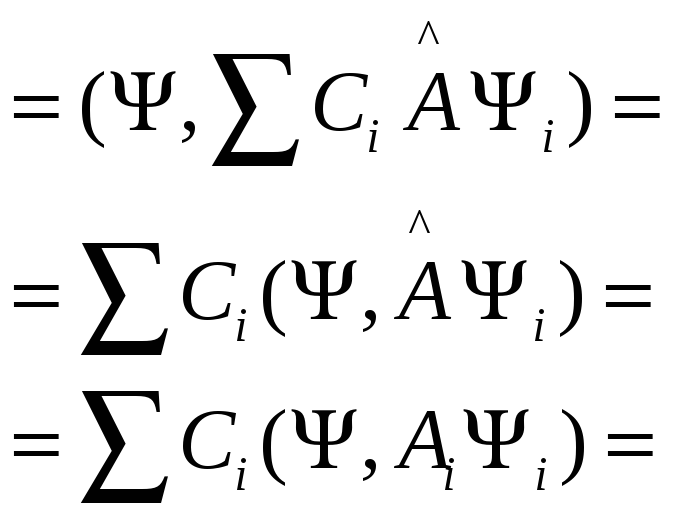
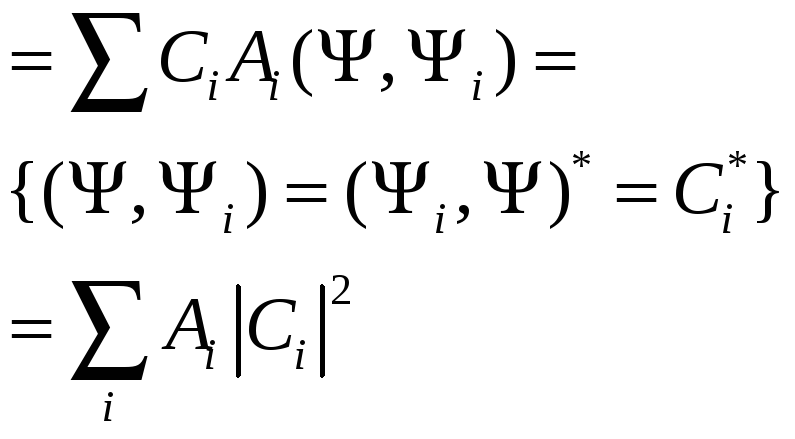
 (4)
(4)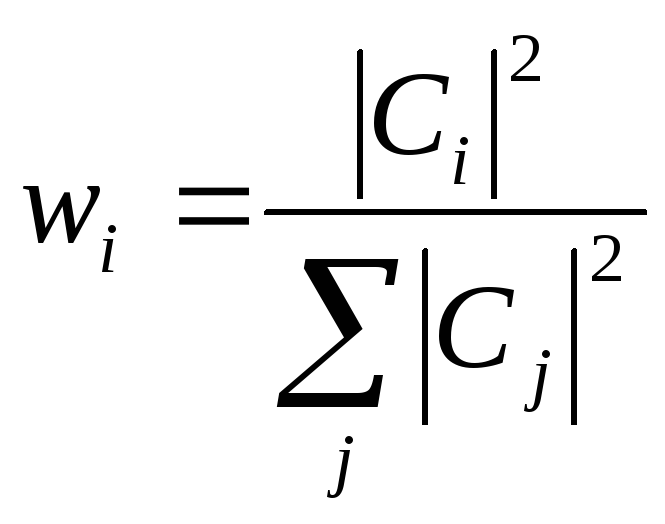
 .
.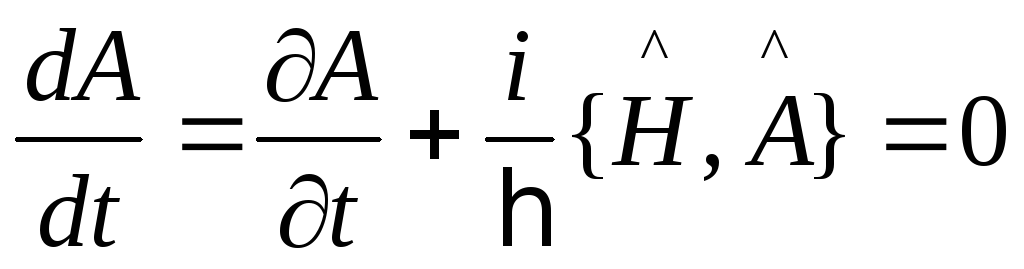
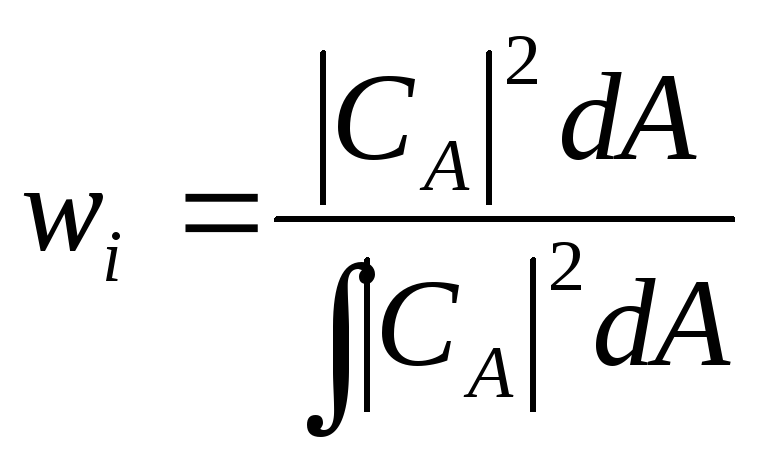

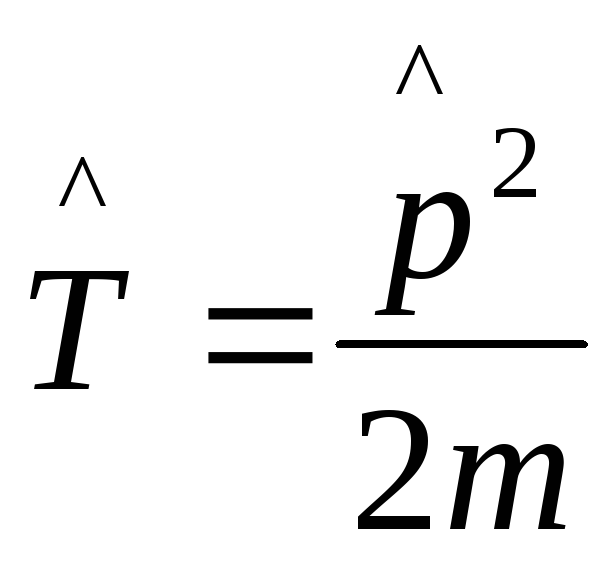
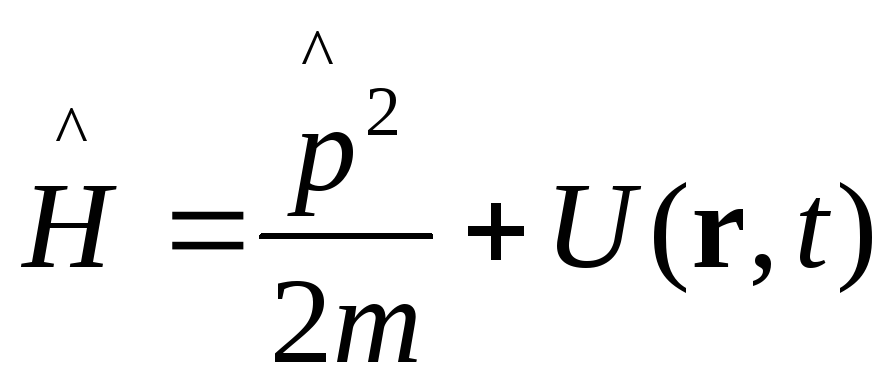 .
Тут присутствует
.
Тут присутствует
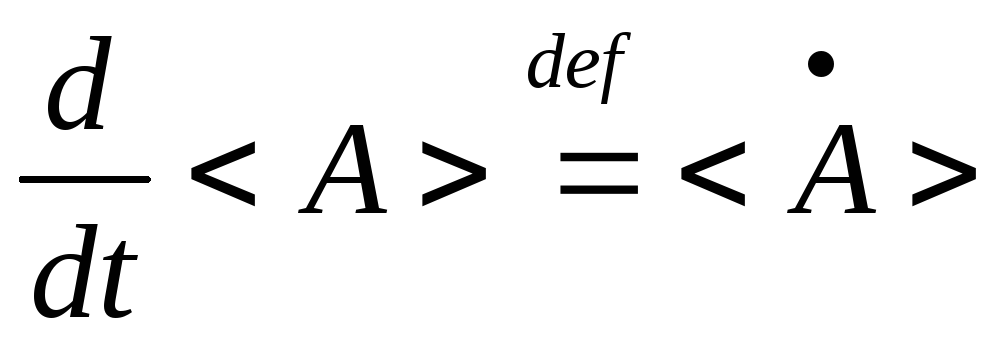 .
.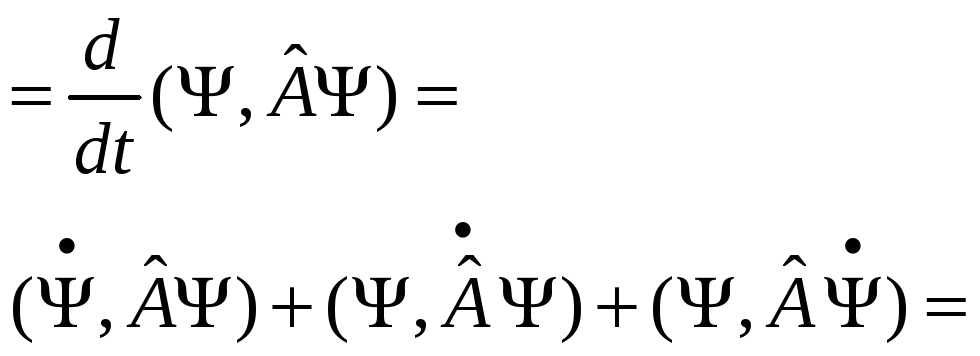 {
{ ,но
,но
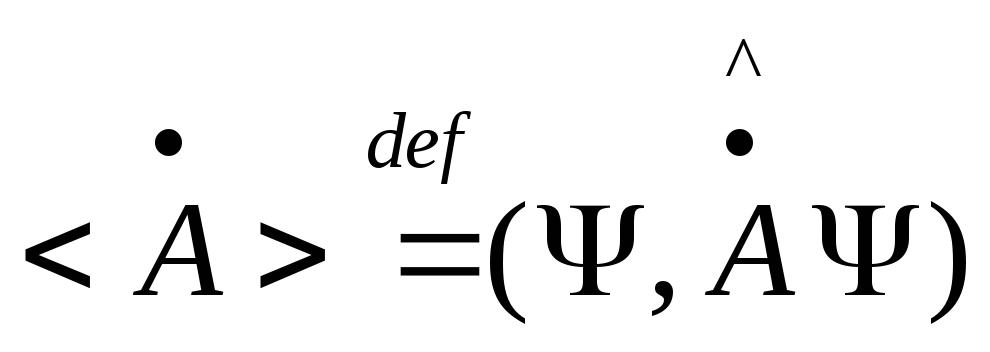 ,
тогда
,
тогда


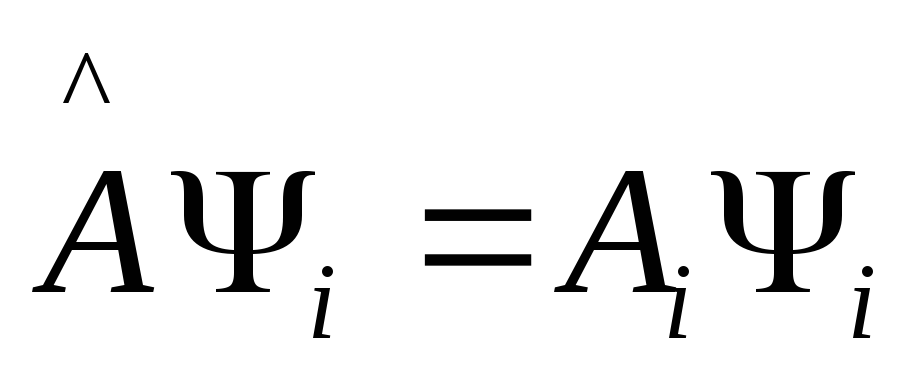 (1)
(1)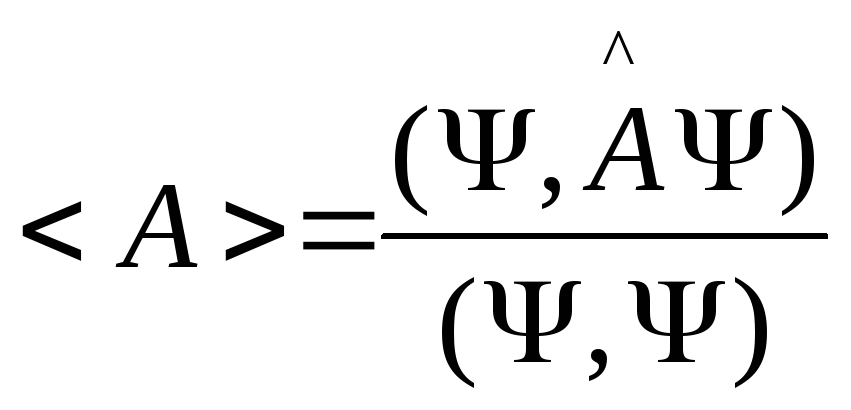 .
Если речь идет о физической величине,
то
.
Если речь идет о физической величине,
то
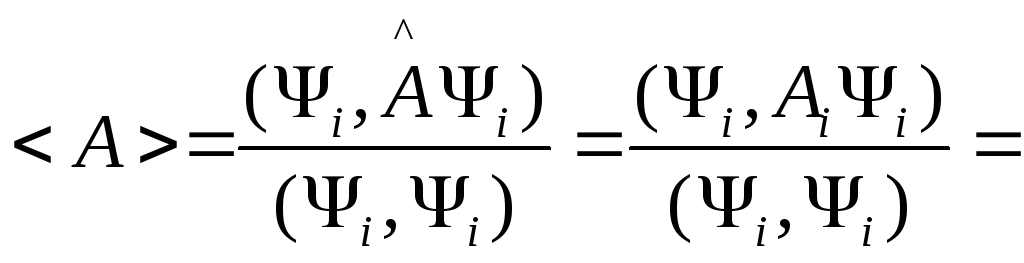
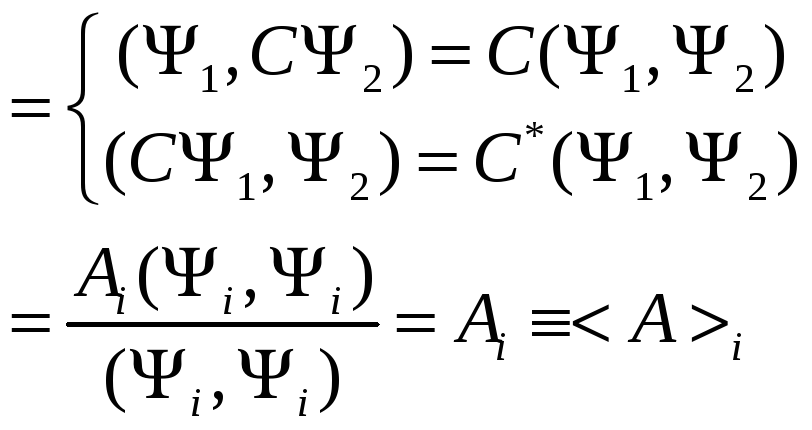 - это среднее значение величины
- это среднее значение величины
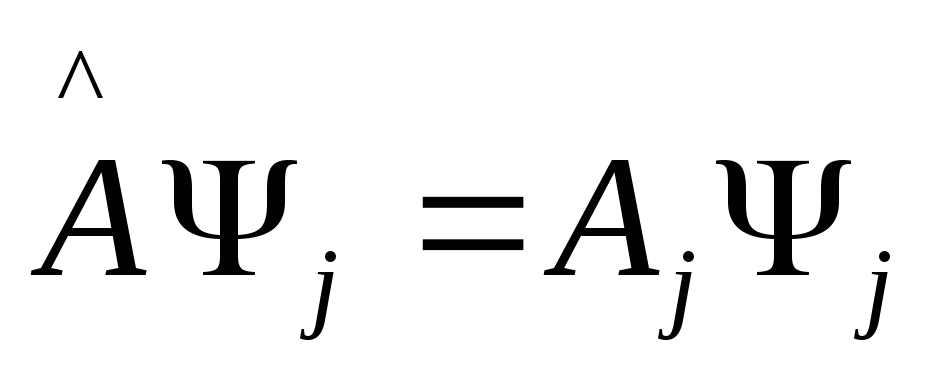
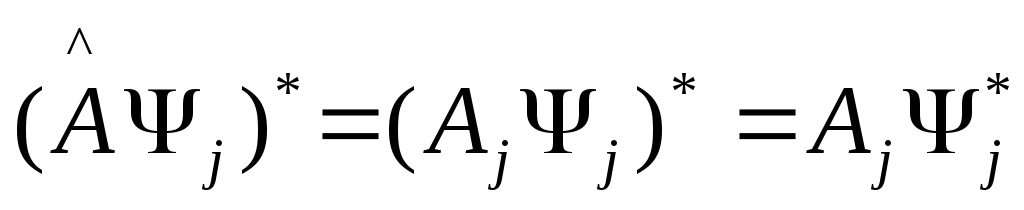 (2)
(2)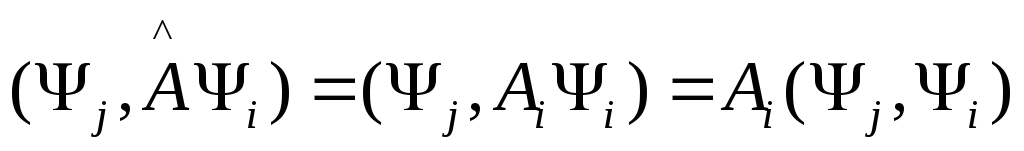 (3)
(3) (4)
(4) (5)т.к.
(5)т.к.
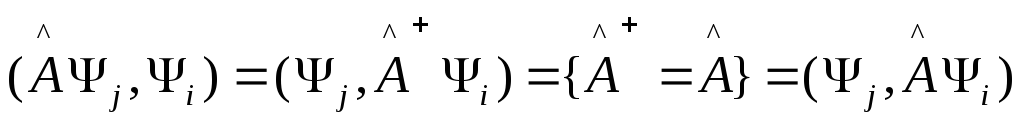 Из
5 имеем
Из
5 имеем
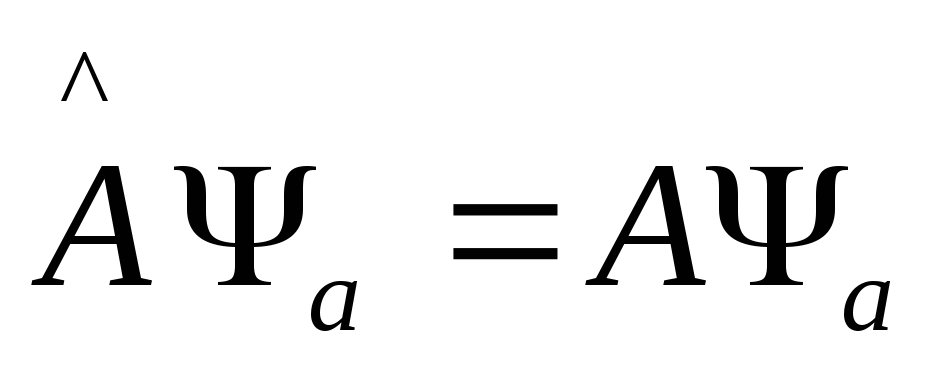 -
у собственной функции индексом является
собственное значение. Собственные
значения непрерывны, они сплошь
заполняют соответствующую числовую
ось.
-
у собственной функции индексом является
собственное значение. Собственные
значения непрерывны, они сплошь
заполняют соответствующую числовую
ось.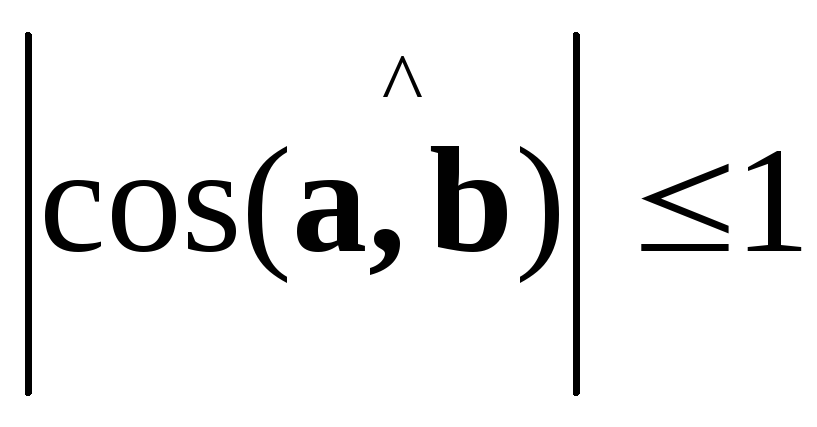 .
. Теперь
если определить
Теперь
если определить
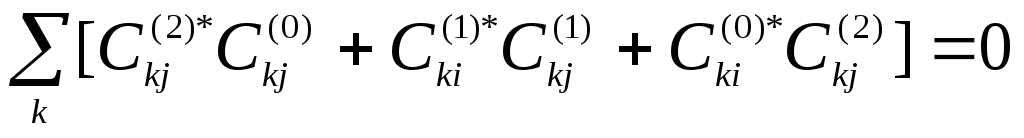 (10*)Рассмотрим
случай
(10*)Рассмотрим
случай
 Получили
поправку второго порядка малоси к
энергетическому уровню основного
состояния. Пусть j-
основное состояние
Получили
поправку второго порядка малоси к
энергетическому уровню основного
состояния. Пусть j-
основное состояние
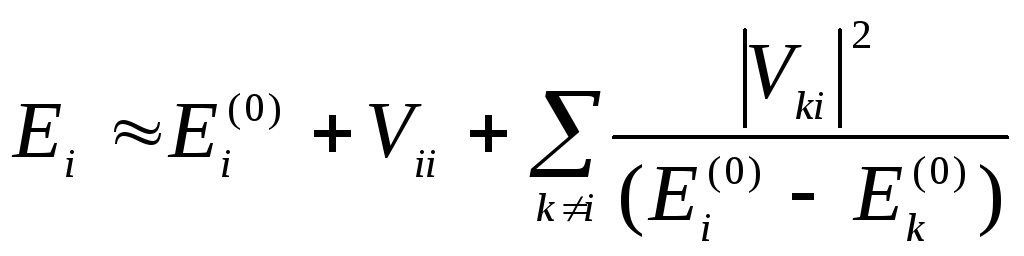 .
. Рассмотрим
случай
Рассмотрим
случай
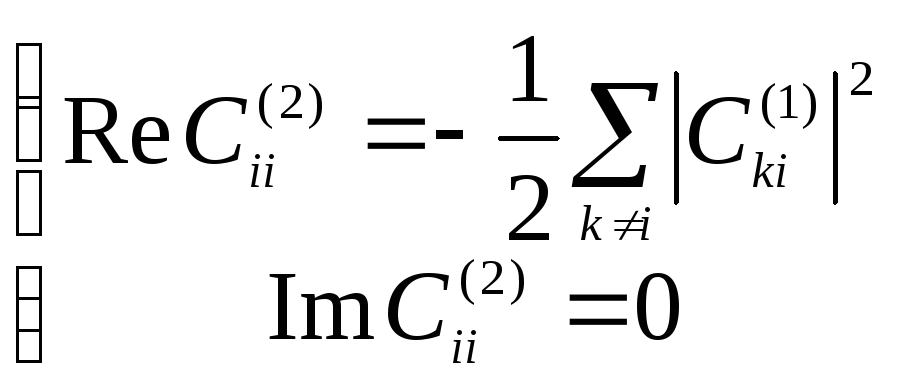 (11*)
(11*)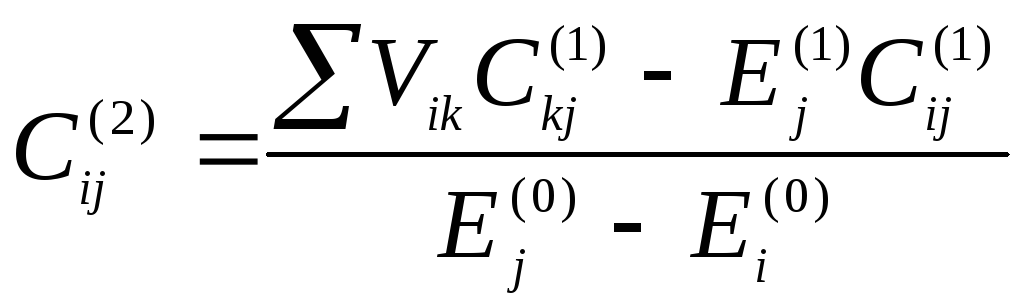
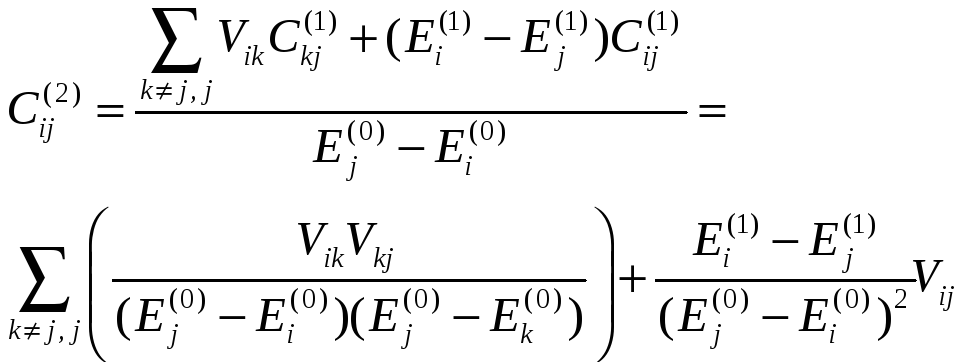 Тогда
Тогда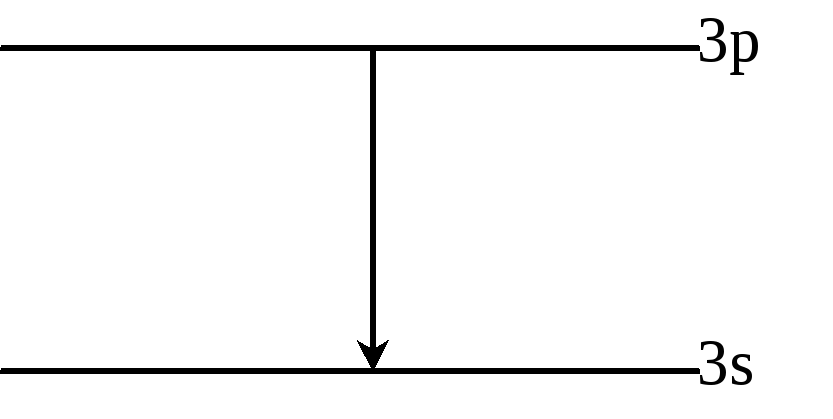
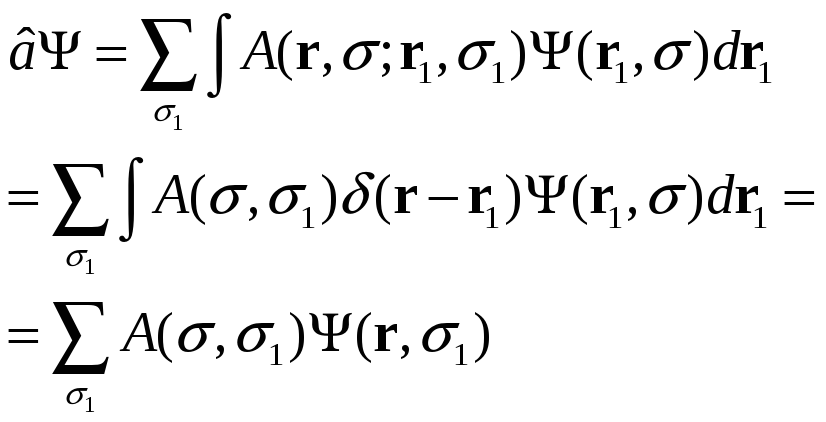 Тогда
Тогда