Задача№7

Електропривод працює в усталеному режимі, що характеризується координатами точки А механічної характеристики 1 двигуна (рис.12), рівняння якої має вигляд ω = ω₀₁ - М/β₁. Двигун навантажений постійним за величиною реактивним статичним моментом М_с. Треба розрахувати і побудувати графіки ω(t) и М(t) змінення в часі швидкості обертання та електромагнітного моменту двигуна від початкових ω_поч і М_поч до кінцевих ω_кін і М_кін значень в перехідному процесі, якій виникає при миттєвому переводі двигуна на механічну характеристику 2, рівняння якої має вигляд ω = ω₀₂ - М/β₂. Значення швидкостей ω₀₁ і ω₀₂ обертання двигуна при ідеальному холостому ході, модулей β₁ і β₂ жорсткості механічних характеристик 1 і 2, приведеного до валі двигуна підсумовного моменту інеції J електропривода та величини М_с статичного моменту наведені в табл.9.

Таблиця 9

Номер варіанта	ω01, рад/с	1, Н·м·с	ω02, рад/с	2, Н·м·с	Mс, Нм	J, кг·м2
17	104,66	7,64	0	1,8	150	10,0

Розв’язок:

Рівняння статичної механічної характеристики двигуна

ω = ω₀ - М/β,

де β - модуль жорсткості цієї характеристики.

Початкову швидкість знайдемо з закону змінення першого графіку. В сталому режимі електромагнітний момент дорівнює статичному (М = М_с):

ω_поч = ω₀₁ - М_с/β₁ = 104,66 - 150/7,64 = 85 рад/с.

Знаходимо швидкість усталеного режиму на другому графіку:

ω_уст = ω₀₂ - М_с/β₂ = 0 - 150/1,8 = -83,3 рад/с.

При М_с = Const електромеханічна постійна часу електропривода:

Т_м = J/β₁ = 10/7,64 = 1,31 c.

Момент короткого замикання:

М_кз = β₁ω₀₁ = 7,64104,66 = 799,6 Нм.

Функція ω(t) є рішенням диференційного рівняння:

Т_м(dω/dt) + ω = ω_уст.

У процесі розгону двигуна із непорушного стану до усталеної швидкості при ω₀ = Const рішення рівняння (2.59) має вигляд:

ω = ω_поч + ω_уст(1 - ).

ω(t) = 85- 83,3(1 - ) рад/с.

Закон змінення електромагнітного моменту в часі:

М(t) = М_кз – β₂ω(t) = М_кз – β₂ω_поч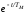 + β₂ω_уст(1 - )

М(t) = 799, 6 – 153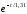- 149,94 (1 -) Н·м.

Рисунок 13, 14

Задача№8

Електромагнітний момент електродвигуна змінюється в часі за законом: М(t) = a + bt. Статичний момент М_с постійний за величиною, реактивний, не перешкоджуючий руху в позитивному напрямку. Визначити закон w(t) змінення кутової швидкості обертання двигуна та побудувати графік функції w(t), якщо початкове значення швидкості w_поч = 0. Поясніть, за яких умов перехідний процес може бути перерваний з переходом в усталений режим.

Значення моменту інерції J механічної частини електропривода, приведеного до швидкості обертання двигуна, величини М_с статичного моменту, коефіцієнтів a, b та постійної часу Т наведені в табл.10.

Таблиця 10

Номер варіанта	J, кг·м2	Mс, Нм	a, Нм	b, Н·м	T, с
17	2,8	240	-380	750	0,01

Розв’язок:

Закон зміни моменту двигуна у часі має вигляд:

М(t) = а + b(1-e^t/T)= -380-750(1-е^t/0,01)

Рівняння руху електроприводадля додатного напрямку руху має вид:

,

або

.

Звідси кутове прискорення буде:

.

Підставимо в заданий закон змінення в часі електромагнітного моменту двигуна. Тоді отримаємо:

.

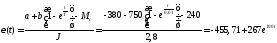Проінтегрувавши вираз , отримаємо шуканий закон ω(t) змінення кутової швидкості обертання двигуна (з урахуванням, що за умовою задачі ω_поч = 0):

.

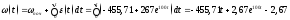За отриманою залежністю побудуємо графік швидкості обертання двигуна від часу ω(t).

Рисунок 15

В початковий момент пуску електропривода пусковий момент перевищує статичний момент, тому пуск двигуна відбувається відразу. Перехідний процес може бути перерваний з переходом в усталений режим за умови, якщо початковий момент двигуна буде меншим, за статичний. Продовж інтервалу часу, коли зберігається співвідношення двигун буде розганятися. Цей інтервал називається часом пуску.