
Московский институт электронной техники
Технический университет
А.Г. Фокин
Теоретическая механика и теория поля
(конспект лекций)
Математический аппарат в теоретической физике (механике).
-
Обобщенные координаты.
-
Описание эволюции системы в конфигурационном пространстве.
Для, того чтобы задать пространственное положение системы нужно координаты. В простейшем случае – декартовые координаты:
М атериальная
точка (м.т.) DN –
число координат, которое необходимое
для
атериальная
точка (м.т.) DN –
число координат, которое необходимое
для
Размер пространства (D) задания координат.
Число точек (N) Связи – любое ограничение, накладываемое на движение системы.
r 1
, rN
; ra=(xa,ya,za);
rai-номер
проекции на ось. x – 1
1
, rN
; ra=(xa,ya,za);
rai-номер
проекции на ось. x – 1
y – 2 D=3
z - 3
Голономные связи – могут быть выражены через координаты точек через равенства:
RN=(r1 … r2)
φα(RN,t)=0 – уравнение k-атой связи. α€[1;k],k – число связей.
Если присоединить время, то связь не стационарная – усложняет теорию.
Стационарные связи.
φα(RN)=0; k-уравнений, k – координаты могут быть выражены через другие. n≡DN-k
n – число степеней свободы – число независимых координат (перемещений), задающих пространству положение системы, они независимы.
Любые независимые переменные, полностью определяющие пространственное положение системы, называется обобщенными координатами.
Плоский математический маятник.


 k
k




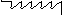 0
Y
0
Y
D =2
=2
n =1
=1
 l
l
 φ
φ
l=√x2 + y2 = const
уравнение связи (голономная)
n=2*1-1=1
 m x=l*cosφ
m x=l*cosφ
y=l*sinφ
X
-
Конфигурационное пространство.
Пространственно обобщенных координат – конфигурационное пр-во (воим – это угол). Как правило ортогонально.
qi , i€[1,n]
q – n-мерный вектор.
 D=3
D=3

 1
1

 q
q
и зображенная 2
зображенная 2
траектория
и
 зображение
зображение
т
 очки
очки
 конфигур. реальное
конфигур. реальное
пр-во
q

q| - полная производная по времени- скорость.
dqi /dt≡q|i ≡ тождественно или по определению.
Эволюция системы – развитие системы – движение изображения точки по изображенной траектории, которая соответствует движению реальных точек в реальном пространстве по реальным траекториям (в механике).
Задачей в механике является описание эволюции системы (механической).
Набор обобщенных координат и скоростей – динамические элементы.
[q + q|] – динамические элементы (переменные).
Этот вариант динамических переменных используется в методе Лагранжа.
Лекция №2 Принцип наименьшего действия
Вариация – изменение функции для данной координаты
Вариации координат и функций.



y=y(x); dy=y/ * dх;
2 dx→0;dy→0;


δy

 y(x)
y(x)
dy
 dx
dx
1
x
В
 ариации
бесконечно малые (произвольные)
ариации
бесконечно малые (произвольные)
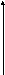
q2 t2
 δq
δq
δq1,δqi;; →δqi в общем случае.
L=L(q) Эйнштейн
F=f(q)=![]()
![]()
t 1
1
q1
Рассмотрим линейную часть по приращению первой вариации.
n=1
δF(q)=F|δq=![]() δq
δq
![]()
![]()
![]() ;
;
![]() ;
;
Принцип наименьшего действия (принцип Гамильтона).
Из всех возможных траекторий движения системы в этом конф. пространстве реализуется та, для которой вариация действия равна 0.
 функционал t.
функционал t.
L – функция Лагранжа (функция динамических переменных)
δS=0![]() уравнения
движения Лагранжа.
уравнения
движения Лагранжа.
Конечные точки траектории зафиксированы→вариации координат в эти моменты равны 0.
![]() ,
,![]() ;
;
![]() ;δ,
;δ,![]() - коммутат. (перестановочные)
- коммутат. (перестановочные)
δqi→![]() ;
;
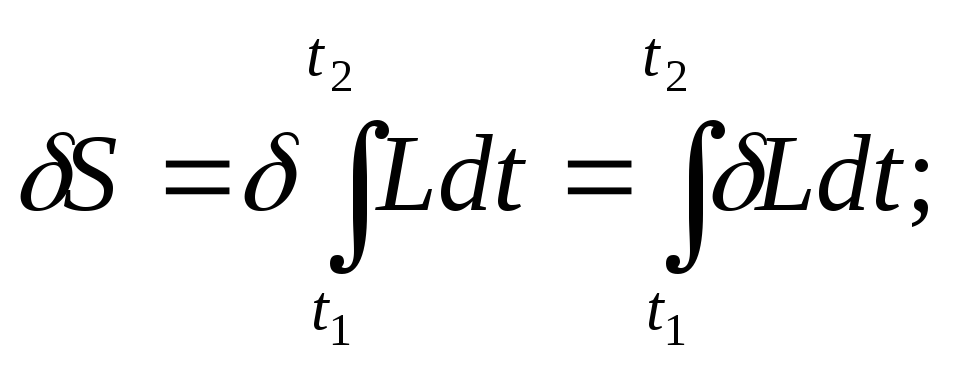
![]() ;
;
![]() ;
;

 -
вариация на концах = 0
-
вариация на концах = 0
 ;подъинтегральное
выражение = 0;
;подъинтегральное
выражение = 0;
![]()
вариации координат
не зависимы линейно. Fi=0
![]() →
→![]()
![]()
Функция Лагранжа и её свойства.
L=T(кинетическая энергия)-U(потенциальная энергия)
U=U(x,t) – внешнее поле не стационарно.
U=U(x) – стационарное поле.
Если U(x)=0 то свободная материальная точка.
1. Уравнение движения Лагранжа инвариантно
![]() ;
;
![]() ;
;![]()
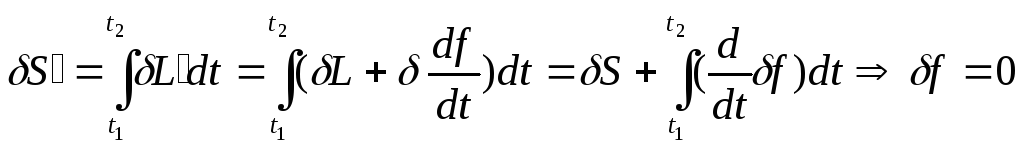 ;т.к.
функции через вариации координат, а они
на концах равны 0.
;т.к.
функции через вариации координат, а они
на концах равны 0.
![]()
Функция Лагранжа простейших систем.
![]() для 1 м.т.
для 1 м.т.
n=D
![]()
система n материальных точек.
Кинетическая энергия материальных точек аддитивна.
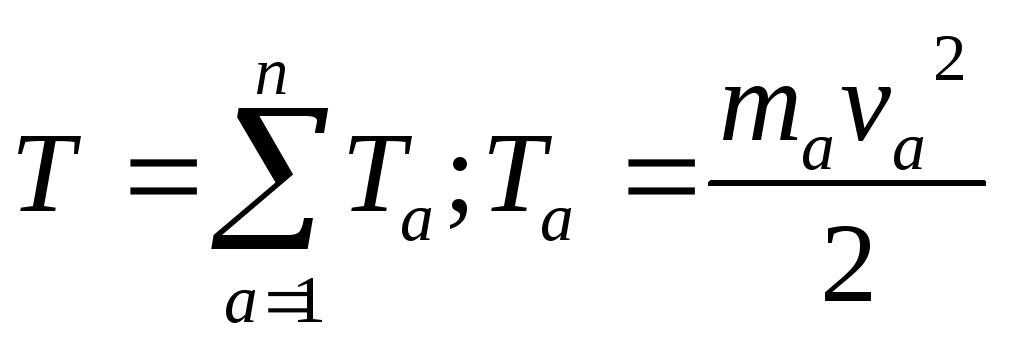
экстенсивный параметр – параметр зависит от размеров системы
потенциальная энергия:
![]()
U включает взаимодействия 1) из вне
2) между частиц (внутри)
внешнее воздействие аддитивно.
![]()
N

 =3 1 2
=3 1 2
![]()
3
N=2: Uint=U12
L=T-U
а) стационарное поле
б) замкнутая система
![]() -
для замкнутой системы
-
для замкнутой системы
Пространство замкнутой системы двух материальных точек.
![]()
одинаковые частицы:m1=m2
![]()
м


 аятник: D=2;n=1
аятник: D=2;n=1
k=1
 ;U=mgl(1-cosθ)
;U=mgl(1-cosθ)
l
θ
m
Можно получить уравнение движения Лагранжа.

рассмотрим малые колебания:
![]()
Свойства симметрии пространства и времени.
Для замкнутой системы реализуются свойства:
-
однородности времени
-
однородности и изотропности пространства.
t1,t2 – начало наблюдения для системы. Для замкнутой системы выбор роли не играет.
Свойства однородности:
![]()
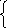
![]() ,τ-время
смещения начала отсчета.
,τ-время
смещения начала отсчета.
f(t)
![]()
![]() -обобщенная
координата,
-обобщенная
координата,
![]() -
обобщенная скорость
-
обобщенная скорость
![]()
используя формулу:
![]()
Интеграл движения.
Рассмотрим функцию динамических переменных и времени.
![]() -
сохраняющая своё значение при эволюции
системы (при движении в конфигурационном
пространстве).
-
сохраняющая своё значение при эволюции
системы (при движении в конфигурационном
пространстве).
Определение:![]()
![]()
интеграл движения 1-я функция динамических переменных и времени, сохраняющая свое значение при движение системы в конфигурационном пространстве по избранной траектории
![]()
в случае стационарных связей этот интеграл движения есть энергия.
Метод Лагранжа T+U=E
Закон сохранения энергии – следствие однородности времени для замкнутой системы.
![]() =0
=0
![]() E=const
– для стационарных внешних полей.
E=const
– для стационарных внешних полей.
