11. Теорема о связи "начальных" и "конечных" значений оригинала и изображения.

Начальное значение оригинала находится по формуле

(18)

Если существует конечный предел , то

(19)

Из соотношений (18) и (19) следует, что для нахождения начальных и конечных значений оригинала не требуется знания оригинала, а достаточно иметь соответствующее изображение. На практике соотношение (19) применяется, например, для нахождения установившегося значения выходного сигнала в системах автоматического регулирования.

Пример. Найти начальное и конечное значения оригинала, которому соответствует изображение .

Согласно (18) и (19)

С другой стороны, из примера (5.7) следует, что

,

поэтому легко убедиться в правильности полученного результата.

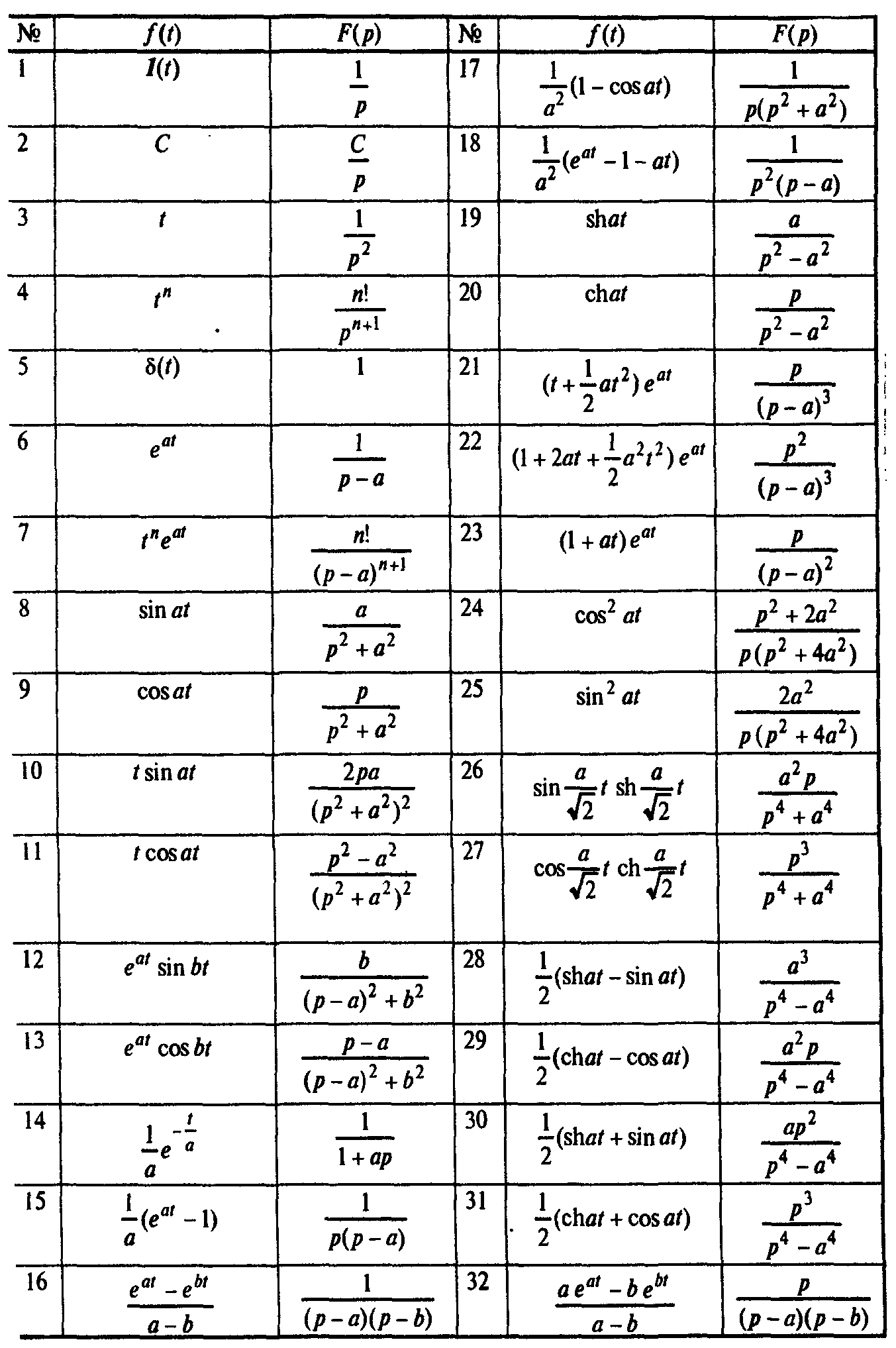
Полученные решения примеров позволяют сформировать таблицу преобразования Лапласа. Таблица является фрагментом более полных таблиц используемых далее при решении примеров и задач.

Нахождение изображения по оригиналу применение таблицы и свойств преобразования лапласа

Для нахождения изображения требуется применить свойства преобразования Лапласа так, чтобы к функции или ее составляющим можно было применить результаты, содержащиеся в таблице.

Таблица

Нахождение изображений периодических функций

Во многих приложениях используются оригиналы, являющиеся периодическими функциями.

Пусть - оригинал с периодом Т (рис.6, а), образованный повторением функции (рис. 6, б):

Рис. 6

Для нахождения изображения периодической функции следует:

1. Найти изображения функции :

.

2. Найти изображение по формуле

(20)

Решение и систем операционным методом:

Пример 1: найти решения уравнения:

НУ: .

Пример 2: найти решения уравнения:

НУ: .

Пример 3: найти решения системы уравнения:

НУ: .