Otchet_13

Новокузнецкий институт (филиал)

федерального государственного бюджетного образовательного учреждения

высшего профессионального образования

«Кемеровский государственный университет»

Отчет о лабораторной работе №1.3.

«Механические колебания».

Выполнил: студент гр. ПМИ-101

Черепанов Данил Владимирович

Принял: кандидат тех. наук,

доцент кафедры экологии и естествознания Чмелева К. В.

г. Новокузнецк

2011 г.

Лабораторная работа № 1.3

«Механические колебания».

ЦЕЛЬ РАБОТЫ:

0. Выбор физических моделей для анализа движения тел.

1. Исследование движения тела под действием квазиупругой силы.

2. Экспериментальное определение зависимости частоты колебаний от параметров системы.

КРАТКАЯ ТЕОРИЯ:

КОЛЕБАНИЕ - периодически повторяющееся движения тела. ПЕРИОД T - минимальное время, через которое движение полностью повторяется.

ГАРМОНИЧЕСКОЕ КОЛЕБАНИЕ - движение, при котором координата тела меняется со временем по закону синуса или косинуса: .

Основными характеристиками гармонических колебаний являются:

АМПЛИТУДА А₀ – максимальное значение параметра А.

ЦИКЛИЧЕСКАЯ ЧАСТОТА собственных колебаний ₀ - в 2 раз большая обычной или линейной частоты  = 1/Т ( - число полных колебаний за единицу времени).

ФАЗА (₀t + ₀) – значение аргумента косинуса.

НАЧАЛЬНАЯ ФАЗА ₀ – значение аргумента косинуса при t = 0.

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ свободных гармонических колебаний параметра А: 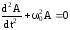, свободных затухающих колебаний:

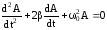, где  - коэффициент затухания .

МАТЕМАТИЧЕСКИЙ МАЯТНИК (ММ) и ПРУЖИННЫЙ МАЯТНИК (ПМ) это МОДЕЛИ объектов, в которых могут происходить гармонические колебания.

ММ это материальная точка, подвешенная на идеальной (невесомой и нерастяжимой) нити.

ПМ это материальная точка, прикрепленная к идеальной (невесомой и подчиняющейся закону Гука) пружине. Формулы для ₀ в этих системах выпишите из конспекта или учебника.

Ход работы:

b= 0,8 кг\с, ₀=20^о, х₀=10 см, m=0,5 кг, L₀=150 см, N=3.

Таблица 1. Результаты измерений (нить).

Номер измерения	N=3
	L(м)	∆t(с)	Т(с)	Т2(с2)
1	1,5	7,40	2,49	6,2
2	1,4	7,30	2,40	5,76
3	1,3	6,95	2,31	5,34
4	1,2	6,55	2,22	4,93
5	1,1	6,40	2,12	4,49
6	1	6,15	2,02	4,08
7	0,9	5,85	1,92	3,69
8	0,8	5,35	1,81	3,28
g (м/с2)	10

Таблица 2. Результаты измерений (пружина).

Номер измерения	N=3
	k(H/м)	∆t(с)	Т(с)	(1/с)	2(1/с2)
1	10	4,15	1,43	4,5	20
2	9	4,35	1,51	4,2	18
3	8	4,70	1,60	4	16
4	7	4,95	1,72	3,7	14
5	6	5,15	1,86	3,5	12
6	5	5,40	2,05	3,2	10

График зависимости квадрата периода колебаний от длины нити ММ.

L(м)

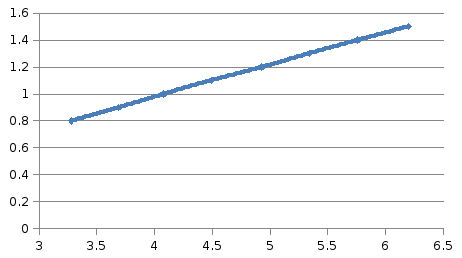
Т₂(с²)

График зависимости квадрата циклической частоты колебаний от коэффициента жесткости пружины ПМ.

k(H/м)))))

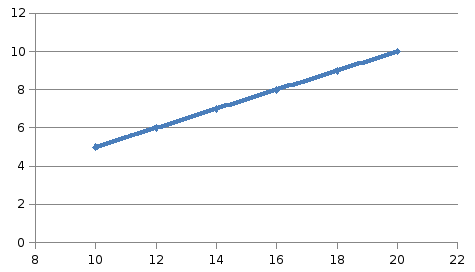
²(1/с²)

1)

,

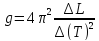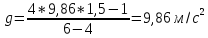
∆g_ош.=0,14 м/с²

2)

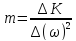
∆m_ош.= 0.

Выводы по графикам:

1) Полученный экспериментально график зависимости квадрата периода колебаний

от длины нити ММ имеет вид прямой и качественно совпадает с теоретической зависимостью данных характеристик, имеющей вид .

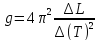2) Полученный экспериментально график зависимости квадрата циклической частоты колебаний от коэффициента жесткости пружины ПМ имеет вид прямой и качественно совпадает с теоретической зависимостью данных характеристик, имеющей вид ^.

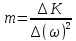Вывод: в данной работе мы экспериментально исследовали движение тела под действием квазиупругой силы, экспериментально определили зависимость частоты колебаний от параметров системы.