Вариант 5

1. Эпицентр циклона, движущийся прямолинейно, во время первого измерения находился в 7 км к северу и 4 км к западу от метеостанции, а во время второго измерения находился в 4 км к северу и 5 км к западу от метеостанции. Определить наименьшее расстояние, на которое эпицентр циклона приблизится к метеостанции.

2. Ветер, дующий в горизонтальном направлении со скоростью 2,8 м/сек, обусловливает подъем некоторой массы кучевых облаков со скоростью 5,6 м/сек. Определите направление и скорость движения облаков.

3.   В лаборатории производится анализ крови. Содержание гемоглобина в крови вычисляется как среднее арифметическое результатов нескольких измерений. Таблица содержит результаты пяти измерений гемоглобина (г/л) в одной пробе крови пациентки.

Номер измерения	1	2	3	4	5
Содержание гемоглобина (г/л)	120	170	100	80	110

а) Найдите среднее арифметическое результатов измерений.

б) Найдите дисперсию измерений.

Выбрано правило: если квадрат отклонения некоторого значения от среднего арифметического превышает дисперсию больше чем в 3,5 раза, то это значение считается ненадежным (выбросом) и в дальнейшем не учитывается.

в) Определите, является ли значение 170 ненадежным в соответствии с выбранным правилом.

г) Найдите среднее арифметическое всех надежных значений.

д) Нормальное содержание гемоглобина в крови мужчины 130–170 г/л. Можно ли считать, что у данного пациента нормальное содержание гемоглобина?

4. Изменение массы вещества при радиоактивном распаде характеризуется формулой:

m(t)=m_0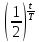.Период полураспада радиойода Т=8 суток. Сколько радиойда останется через 10 суток, если его начальная масса равна 100 г?

5. Дана матрица перераспределения населения между четырьмя районами:

.

а) Найти количество людей, переехавших из третьего района.

б) Найти количество людей, приехавших во второй район.

в) Найти количество всех переехавших.

6. А) Из цифр 1, 2, 3, 4, 5 составляются всевозможные числа, каждое из которых содержит не менее трех цифр. Сколько таких чисел можно составить, если повторения цифр в числах запрещены?

Б) Сколько существует различных автомобильных номеров, которые состоят из пяти цифр, если первая из них не равна нулю?

В) Абонент забыл последние две цифры номера телефона, и помня лишь, что эти цифры различные и четные, набрал их наудачу. Сколько вариантов набора номера существует?

_{7 .Агрофирма закупает огурцы в двух теплицах. 70% огурцов из первой теплицы – огурцы высшей категории, а из второй теплицы – 80% огурцов высшей категории. Всего высшую категорию получает 72% огурцов. Найдите вероятность того, что огурец, купленный у этой агрофирмы, окажется из первой теплицы.}