Лекции 2 курс / Лекция 5

Лекция 5.

Числовые характеристики дискретной случайной величины. Математическое ожидание.

Математическое ожидание дискретной случайной величины.

Определение 5.1. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.

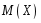Пусть случайная величина может принимать только значения , вероятности которых соответственно равны . Тогда математическое ожидание случайной величины определяется равенством

Замечание. Из определения следует, что математическое ожидание дискретной величины есть неслучайная (постоянная) случайная величина.

Пример 1. Найти математическое ожидание случайной величины , зная закон ее распределения

X	3	5	2
p	0,1	0,6	0,3

Решение. Искомое математическое ожидание равно сумме произведений всех возможных значений случайной величины на их вероятности:

Пример 2. Найти математическое ожидание числа появлений события в одном испытании, если вероятность события равна .

Решение. Случайная величина - число появлений события в одном испытании, может принимать только два значения (событие наступило) с вероятностью и 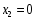(событие не наступило) с вероятностью .

Искомое математическое ожидание

Вероятностный смысл математического ожидания.

Пусть произведено испытаний, в которых случайная величина приняла раз значение , раз значение , …, 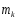раз значение , причем . Тогда среднее арифметическое всех значений, принятых равно

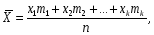
или

При большом числе испытаний

Тогда

Математическое ожидание приближенной равно среднему арифметическому наблюдаемых значений случайной величины.

Свойства математического ожидания

Свойство 1. Математическое ожидание постоянной величины равно самой постоянной

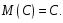
Свойство 2. Постоянный множитель можно выносить за знак математического ожидания

Определение 5.2. Две случайные величины называются независимыми, если закон распределения одной их них не зависит от того, какие возможные значения приняла другая величина.

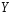Определение 5.3. Произведением двух независимых случайных величин и называется случайная величина 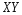, возможные значения которой равны произведениям каждого возможного значения величины на каждое возможное значение величины ; вероятности возможных значений произведения равны произведениям вероятностей возможных значений сомножителей.

Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий

Пример 3. Независимые случайные величины 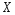и заданы следующими законами распределения

X	5	2	4
p	0,6	0,1	0,3

Y	7	9
p	0,8	0,2

Найти математическое ожидание величины .

Решение.

Случайная величина задана законом распределения

XY	35	45	14	18	28	36
p	0,48	0,12	0,08	0,02	0,24	0,06

Найдем математическое ожидание каждой из величин и :

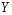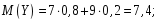
Тогда

Определение 5.4. Суммой двух случайных величин и называется случайная величина , возможные значения которой равны суммам каждого возможного значения величины с каждым возможным значением величины ; вероятности возможных значений суммы 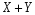для независимых величин равны произведениям вероятностей слагаемых, для зависимых величин – произведениям вероятности одного слагаемого на условную вероятность второго.

Свойство 4. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий

Пример 4. Производится 3 выстрела с вероятностями попадания в каждом из них . Найти математическое ожидание общего числа попаданий.

Решение. Число попаданий при первом выстреле есть случайная величина , которая может принимать только два значения: 1 (попадание) с вероятность и 0 (промах) с вероятностью . Математическое ожидание числа попаданий при первом выстреле равно вероятности попадания ( см. пример 2), т.е. .

Аналогично найдем математические ожидания числа попаданий при втором и третьем выстрелах:

Общее число попаданий есть также случайная величина, состоящая из суммы попаданий в каждом из трех выстрелов:

Тогда

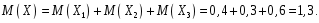
Пример 5. Найти математическое ожидание суммы числа очков, которые могут выпасть при бросании двух игральных костей.

Решение. Обозначим число очков, которое выпадет на первой кости, через и на второй кости – через 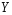. Возможные значения этих величин одинаковы и равны 1, 2, 3, 4, 5 и 6, причем вероятность каждого из этих значений равна 1/6.

Тогда математическое ожидание числа очков, которые могут выпасть на первой кости:

Очевидно, что и

Искомое математическое ожидание

Пусть производится независимых испытаний, в каждом из которых вероятность появления события постоянна равна .

Теорема 5.1. Математическое ожидание числа появлений события в независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании

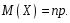
Замечание. Так как величина распределена по биномиальному закону, то теорему можно сформулировать так: математическое ожидание биномиального распределения с параметрами и равно .

Пример. Вероятность попадания в цель при стрельбе из орудия равна 0,6. Найти математическое ожидание общего числа попаданий, если будет произведено 10 выстрелов.

Решение. Попадание при каждом выстреле не зависит от исходов других выстрелов, поэтому рассматриваемые события независимы и, следовательно

Теорема 5.2. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю: