Вариант №6

1. Найти распределение случайной величины 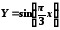, где- число очков, выпадающее при бросании игральной кости. Построить многоугольник распределения и вычислить математическое ожидание.

2. Пусть случайные величины и - независимы и их распределение задано таблицами:

	0	1	2			2	4
	0,2	0,4	0,4			0,6	0,4

Найти: 1) ряд распределения случайной величины ; 2) построить функцию распределения; 3) вычислить вероятность; 4) найти.

3. Случайная величина задана функцией распределения вероятностей:

.

Найдите параметр и плотность распределения вероятностей, постройте кривую распределения. Вычислите математическое ожидание, дисперсию этой случайной величины. Найдите вероятность события.

4. Химический завод изготавливает серную кислоту номинальной плотности 1,84 г/см³. В результате статистического исследования обнаружено, что практически 99,9% всех выпускаемых реактивов имеют плотность в интервале (1,82; 1,86). Найти вероятность того, что кислота удовлетворяет стандарту, если для этого достаточно, чтобы ее плотность не отклонялась от номинала более чем на 0,01 г/см³.

5. В автопарке 200 автомобилей. Каждый из них за время эксплуатации может выйти из строя, независимо от других, с вероятностью 0,04. Оцените вероятность того, что доля надёжных автомобилей отличается по модулю от вероятности безотказной работы любого из них не более чем на 0,1.

Вариант №7

1. В партии из 10 изделий 3 бракованных. Наудачу отобрали для проверки их качества 3 изделия. Случайная величина – число бракованных изделий среди отобранных. Для этой случайной величины: 1) составить закон распределения; 2) найти функцию распределения; 3) найти вероятность того, что число бракованных изделий не менее двух; 4) вычислить среднее число бракованных изделий; 5) найти моду.

2. Игра заключается в том, что монету бросают до появления герба. Если герб выпал при 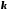-ом бросании монеты, то игрокполучаетрублей от игрока. Сколько рублей должен уплатить игрокигрокуперед началом игры для того, чтобы игра была безобидной (математическое ожидание проигрыша каждого игрока равно нулю)?

3. Пусть - непрерывная случайная величина с плотностью распределения вероятностей при идля. Постройте кривую распределения вероятностей. Найдите: 1)коэффициент ; 2) математическое ожидание ; 3) функцию распределения и постройте её график; 4) моду.

4. Цена некоторой ценной бумаги имеет нормальное распределение. В течение последнего года 20% рабочих дней она была ниже 88 ден.ед., а 75% – выше 90 ден.ед. Найти математическое ожидание и дисперсию цены ценной бумаги.

5. Вероятность производства бракованного изделия равна 0,05. Оценить вероятность того, что в партии из 1000 изделий число бракованных отличается от своего среднего значения менее чем на 5 изделий.

Вариант №8

1. В урне 3 белых и 2 черных шара. Из нее последовательно вынимают шары до первого появления белого шара. Случайная величина – число извлеченных шаров. Для этой случайной величины составить закон распределения, найти функцию распределения и построить её график. Вычислить математическое ожидание и моду. Найти вероятность того, что извлекли более двух шаров.

2. Считая, что вес тела с одинаковой вероятностью может быть равен любому целому числу граммов от 1 до 10, определите при какой из двух систем разновесов: 1) 1, 2, 2, 5, 10; 2) 1, 2, 3, 4, 10 – среднее число необходимых для взвешивания гирь будет наименьшим, если при взвешивании разрешается гири ставить только на одну чашу весов, а подбор гирь при взвешивании осуществляется так, чтобы использовать наименьшее возможное число гирь.

3. Случайная величина задана плотностью 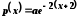дляипри. Найти: 1) коэффициент ; 2) постройте кривую распределения вероятностей; 3) математическое ожидание ; 4) моду.

4. Случайная величина ~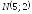. Постройте кривую распределения для этой случайной величины и вычислите: 1) ; 2) ; 3) для случайной величины вероятность. Постройте эскизы кривых распределения указанных случайных величин.

5. Вероятность того, что покупателю магазина женской одежды необходим 44 размер, равна 0,4. Оценить вероятность того, что доля покупателей одежды данного размера отклонится по абсолютной величине от вероятности этого события, не менее чем на 0,1, если всего в магазине ожидается 1000 покупателей.