1. Метод деления отрезка пополам (метод бисекций или дихотомия).

Простейшим и надежным алгоритмом уточнения корня на отрезке [a, b], если f(x) - непрерывная функция и f(a)f(b)<0, является метод деления отрезка пополам.

Очевидно, что середина отрезка служит приближением к корню уравнения (1) с точностью e<(b-a)/2. В середине отрезка x₁=(a+b)/2 определяется знак функции f(x), затем выбирается та половина отрезка [a, (a+b)/2] или [(a+b)/2,b], на концах которой функция f(x) принимает значения разных знаков, и деление повторяется.

Если требуется найти корень с точностью e, то деление отрезка продолжается до тех пор, пока длина отрезка не станет меньшей 2e.

Тогда середина последнего отрезка даст значение корня с требуемой точностью. В этом методе можно не вычислять значения функции f(x), достаточно лишь определить знак функции.

2. Метод хорд (метод линейной интерполяции).

В этом методе нелинейная функция f(x) на отделенном интервале [a, b] заменяется линейной, в качестве которой берется хорда – прямая , стягивающая концы нелинейной функции. Эта хорда определяется как прямая, проходящая через точки с координатами (a, f(a)) и (b, f(b)), т.е. делит отрезок [a, b] пропорционально величинам ординат ,f(a) и ,f(b),.

Имея уравнение хорды y=cx+d, можно легко найти точку ее пересечения с горизонтальной осью, подставив в уравнение хорды y=0 и найдя из него х. Естественно, в полученной таким путем точке х₁ не будет решения, ее принимают за новую границу отрезка, где содержится корень. Через эту точку с координатами (х₁, f(х₁)) и соответствующую границу предыдущего интервала опять проводят хорду, находят х₂, и т. д. несколько раз, получая последовательность х₃, х₄, х₅, , сходящуюся к корню.

Метод применим только для монотонных функций.

Алгоритм метода зависит от свойств функции f(x) .

Если f(b)f’’(b)>0, то строящаяся на каждом этапе хорда имеет правый фиксированный (закрепленный) конец. Для определенности f’’(x)>0 (обратный случай сводится к первому, если записать уравнение –f(x)=0). Тогда кривая y=f(x) будет выпукла вниз, т. е. расположена ниже своей хорды (см. рис.1).

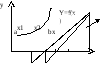
Рис.1

Итак, если f(b)>0, то алгоритм выглядит следующим образом:

Применяя этот прием к тому из отрезков [a, x₁] или [x₁, b], на концах которого функция f(x) имеет противоположные знаки, получим второе приближение корня x₂ и т. д. При этом последовательность x₁, x₂, будет приближаться к корню слева, (в качестве x₀ можно выбрать начало отрезка точку а).

Если f(a)f’’(a)>0, то строящаяся на каждом этапе хорда имеет левый фиксированный конец и алгоритм выглядит следующим образом:

При этом последовательность x₁, x₂, будет приближаться к корню справа, в качестве x₀ можно выбрать точку b)

Приведем формулу оценки абсолютной погрешности приближенного значения х_i , если известны два последовательных значения x_i и x_i+1.

Теоретически доказано, что если первые производные на концах интервала при монотонной и выпуклой функции f(x) не различаются более, чем в два раза, то справедливо соотношение |x^* - x_i | < |x_i - x_i-1| и условием прекращения итераций может быть |x_i - x_i-1 | £ e, а в качестве корня принято x_i+1 (можно также окончить процесс и при достижении f(x_i) £e). Таким образом, как только будет обнаружено, что

|x_i - x_i-1 | £ e, где e - заданная погрешность, то гарантировано, что |x - x_i | £ e.