Обусловленность матрицы. Погрешности.

Числа обусловленности матрицы определяют чувствительность решения системы линейных уравнений к погрешностям исходных данных. Следующие функции позволяют найти числа обусловленности матриц.

Значение cond(X), близкое к 1, указывает на хорошо обусловленную матрицу;

Вернемся к анализу формулы (4) для вариации решения x

1. Пусть матрица А известна точно (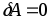) и погрешность решения связана лишь с погрешностью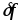правой части, тогда:

Из:

Перемножая полученные неравенства, найдем:

Или

=M/m - число обусловленности матрицы А.

 

- всегда (в любой норме), т.о. хорошо обусловленные матрицы – это матрицы с малым , при этом относительная погрешность решения мала.

2. Пусть известно возмущение 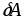матрицыА, при условии, что правая часть f задана точно.

Тогда:

Или

 

Таким образом, чем больше число обусловленности, тем чувствительнее система к округлениям.

 

Системы с большим числом обусловленности называют плохо обусловленными.

 

В случае СЛАУ 2-го порядка понятие обусловленности матрицы допускает наглядную геометрическую интерпретацию.

 

Лекция №3

Метод последовательного исключения неизвестных – метод Гаусса.

Методы решения систем линейных алгебраических уравнений (СЛАУ): 1) точные (прямые) 2)приближенные ( методы последовательных приближений.)

Прямые методы : метод Крамера, метод Гаусса и его модификации: (метод главного элемента, метод квадратного корня, метод отражений и другие), метод ортогонализации. N £ 10³.

Методы последовательных приближений (итерационные):

метод простой итерации,

метод Зейделя,

метод релаксаций,

градиентные методы и их модификации. N¸ 10⁶.

Рассмотрим систему n линейных алгебраических уравнений с n неизвестными:

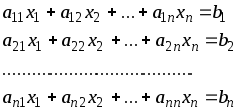(1)

в матричном виде: Ax = b;

здесь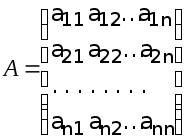- квадратная матрица размераn´n,

, - векторы n-го порядка.

В индексной форме:

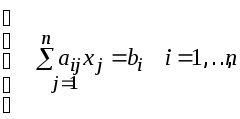(2)

Система линейных уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной (противоречивой), если она не имеет решений.

Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если более одного решения.

1. Схема единственного деления

Делим первое уравнение этой системы на коэффициент a₁₁ ¹ 0 при неизвестном х₁ (ведущий элемент).

Выполнения условия a₁₁¹ 0 можно добиться всегда путем перестановки уравнений системы.

(3) или

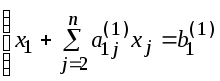
Исключаем неизвестное х₁ из остальных уравнений системы (для этого достаточно из каждого уравнения (i =2,3,…,n) вычесть уравнение (3), предварительно умноженное на коэффициент при х₁ , т.е. на a₂₁, a₃₁ и т.д. a_i1,

Например:

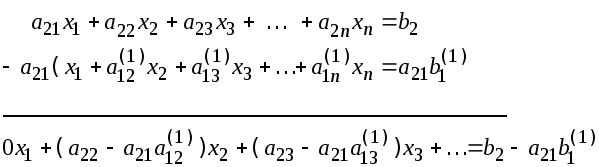
Обозначим

Преобразованные уравнения будут иметь вид:

Здесь обозначено

Матрица системы имеет вид:

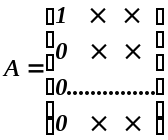
Вслед за этим, оставив первое уравнение в покое, над остальными уравнениями системы совершим аналогичные преобразования:

1. выберем из их числа уравнение с ведущим элементом a₂₂⁽¹⁾

2. и исключим с его помощью из остальных уравнений неизвестное х₂.

3. Повторяя этот процесс n раз, вместо системы (2) получим равносильную ей систему с треугольной матрицей:

(4)

Матрицы такого вида называются верхними треугольными матрицами.

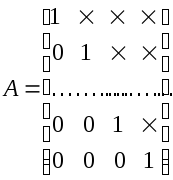
Из системы (4) последовательно находятся значения всех неизвестных x_n, x_n-1, ..., x₁.

Таким образом, процесс решения (1) по методу Гаусса распадается на два этапа. Первый этап, состоящий в последовательном исключении неизвестных, называют прямым ходом. (число арифметических действий ¸ 2N³/3)

Обратным ходом. (число арифметических действий ¸ N²)

Общие формулы обратного хода имеют вид: