
- •Лекция №1
- •§ 1. Задача вычисления.
- •§ 2. Абсолютная и относительная погрешности
- •§ 3. Неустранимая погрешность значения функций для приближенных значений аргументов. Погрешности арифметических операций.
- •Лекция №2 Численные методы линейной алгебры
- •Формальное решение. Устойчивость.
- •Обусловленность матрицы. Погрешности.
- •Лекция №3
- •1. Схема единственного деления
- •3. Расчетные формулы
- •Лекция № 4 Метод Гаусса с выбором главного элемента (оптимальный метод).
- •Применения метода Гаусса к вычислению определителей и обратных матриц.
- •Лекция № 5 Итерационные методы решения систем линейных алгебраических уравнений.
- •Лекция № 6 Метод Зейделя (модификация метода итераций).
- •Тогда условие окончания итерационного процесса Зейделя будет иметь вид:
- •Лекция № 7 Методы решения нелинейных уравнений и систем нелинейных уравнений.
- •1. Метод деления отрезка пополам (метод бисекций или дихотомия).
- •Метод хорд (метод линейной интерполяции).
- •3. Метод Ньютона (метод касательных или метод линеаризации).
- •4. Метод итераций (задача о неподвижной точке).
- •Оценка погрешности приближений:
- •Лекция № 8
- •1. Метод итераций для системы двух уравнений.
- •2. Метод Ньютона для системы двух уравнений.
- •Лекция №9 Алгебраическая проблема собственных значений.
- •Лекция № 10 Приближение функций и их производных.
- •Постановка задачи приближения функций.
- •2. Оценка погрешности полиномиальной интерполяции.
- •Лекция № 11 Интерполяционный многочлен Ньютона с конечными разностями.
- •Лекция № 12 Метод наименьших квадратов и наилучшие среднеквадратические приближения.
- •О нормальной системе мнк при полиномиальной аппроксимации.
- •Лекция №13 Сплайн интерполяция
- •Лекция № 15
- •Метод Эйлера – разные подходы к построению.
- •Методы Рунге – Кутта.
- •Лекция № 16
- •Лекция № 17 Разностные схемы для уравнений параболического типа.
- •Лекция №18
- •Лекция № 19 Разностные схемы для уравнений эллиптического типа.
§ 3. Неустранимая погрешность значения функций для приближенных значений аргументов. Погрешности арифметических операций.
Пусть
![]() - непрерывная дифференцируемая функция
независимых переменных
- непрерывная дифференцируемая функция
независимых переменных![]() .
Если значения аргумента даны неточно,
а приближенно
.
Если значения аргумента даны неточно,
а приближенно
![]() -
имеем неустранимую погрешность, то
вместо
y
из (3) мы получим некоторую величину y*,
-
имеем неустранимую погрешность, то
вместо
y
из (3) мы получим некоторую величину y*,
![]() (6).
(6).
Требуется
найти абсолютную погрешность
![]() ,
и относительную погрешность
,
и относительную погрешность![]() ,
характеризующие неустранимую погрешность
функции (6).
,
характеризующие неустранимую погрешность
функции (6).
Эту
задачу в каждом конкретном случае можно
совершенно строго решить при помощи
методов математического анализа,
исследуя область изменения y
при
![]() .
.
Однако, при более или менее сплошной функции f применение точных методов математического анализа приводит к сложным вычислениям. Поэтому целесообразнее иметь в своем распоряжении приемы, позволяющие решить поставленную задачу более элементарно, хотя м.б. более грубо. Для их применения наложим некоторые дополнительные условия на функцию f и погрешности ее аргументов.
Будем предполагать:
Частные производные f изменяются достаточно медленно.
Относительные погрешности
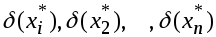 исходных данных достаточно малы.
исходных данных достаточно малы.
По формуле конечных приращений получим:
![]()
где
![]() - значения производных
- значения производных![]() - взятых в некоторой точке отрезка
- взятых в некоторой точке отрезка![]() .Используя
предположение 1), заменим
.Используя
предположение 1), заменим![]() на
на![]() .
.
Получим
![]()
Отсюда
![]() (7)
(7)
Разделим (7) на y* и учитывая 1) и 2), получим приближенную формулу для относительной погрешности функции:
![]() (8)
(8)
Если
применить формулы (7) и (8) к случаю функции
с одной переменной, то мы получим для
оценки ее абсолютной и относительной
погрешностей следующие формулы:
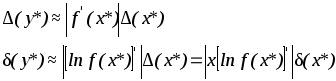
Лекция №2 Численные методы линейной алгебры
Решение систем линейных алгебраических уравнений СЛАУ с невырожденной (квадратной) матрицей.
Нахождение собственных значений и собственных векторов для квадратных матриц – алгебраическая проблема собственных значений.
1) Решение СЛАУ
![]() (1)
(1)
С квадратной невырожденной матрицей:
![]()
Матрица
А
определяет отображение
![]()
2) Вычисление определителя матрицы:
![]() (2)
(2)
3) Нахождение обратной матрицы А-1 для невырожденной квадратной матрицы А:
![]() (3)
(3)
Формальное решение. Устойчивость.
Формальное решение задачи (1) строится по известным формулам Крамера:
![]()
Формальное решение устойчиво, т.е. непрерывно зависит от входных данных A и f .
Действительно,
варьируя
![]() ,
найдем:
,
найдем:
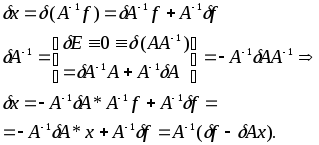
Получаем, что:
![]() (4)
(4)
Таким образом:
![]()
Нормы
Основные используемые
в
![]() нормы:
нормы:
1) Норма вектора x.
Запишем разложение вектора по базису:
![]()
![]() .
.
Базисные вектора образуют строку e , а координаты вектора `x - столбец X
Евклидова норма вектора
![]()
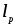 -Норма
(при p=2
норма Гильберта - Шмидта)
-Норма
(при p=2
норма Гильберта - Шмидта)
![]()
(для конечномерного случая 1/n можно перед суммой опустить).
с) c - норма (равномерная или Чебышевская норма вектора x)
![]()
В
![]() имеют место соотношения:
имеют место соотношения:
![]()
т.е.
в
![]() все эти нормыэквивалентны
и сходимость в любой из них влечет
сходимость в остальных нормах.
все эти нормыэквивалентны
и сходимость в любой из них влечет
сходимость в остальных нормах.
Проверим, например:
![]()
Имеем:
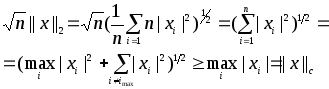
2). Норма матрицы А. Норма матрицы А, согласованная с нормой вектора x определяется следующим образом:
![]()
Отсюда
![]()
Это условие согласования норм ||x|| и ||A||.
Можно проверить, что введенная таким образом норма матрицы удовлетворяет неравенствам:
![]() ,
,
Для
квадратных матриц
![]() наиболее употребительны следующие
нормы:
наиболее употребительны следующие
нормы:
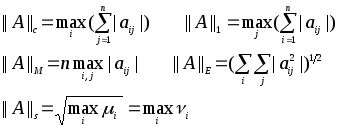
(где
![]() - собственные значения симметричной
самосопряженной матрицы
- собственные значения симметричной
самосопряженной матрицы![]() ,
,![]() ).
).
Первые две нормы не имеют специальных названий:
![]() -
называется максимальной,
-
называется максимальной,
![]() -
сферической
или евклидовой,
-
сферической
или евклидовой,
![]() -
спектральной.
-
спектральной.
Умножая вектор х на матрицу А, получаем новый вектор Ах, норма которого может сильно отличаться от нормы вектора х.
Величину
![]() можно рассматривать как своеобразный«коэффициент
растяжения»
вектора х
матрицей А.
Для некоторых векторов он может быть
малым, а для некоторых большим.
можно рассматривать как своеобразный«коэффициент
растяжения»
вектора х
матрицей А.
Для некоторых векторов он может быть
малым, а для некоторых большим.
Если
M
и m
– максимальное и минимальное значение
коэффициента растяжения, то
![]()
Нормой матрицы А называется максимальное значение коэффициента растяжения:
![]()
Минимальное значение коэффициента растяжения также играет важную роль в линейной алгебре.
Если А – невырожденная матрица, то для нормы обратной матрицы справедливо равенство:
![]()
