
- •Лекция №1
- •§ 1. Задача вычисления.
- •§ 2. Абсолютная и относительная погрешности
- •§ 3. Неустранимая погрешность значения функций для приближенных значений аргументов. Погрешности арифметических операций.
- •Лекция №2 Численные методы линейной алгебры
- •Формальное решение. Устойчивость.
- •Обусловленность матрицы. Погрешности.
- •Лекция №3
- •1. Схема единственного деления
- •3. Расчетные формулы
- •Лекция № 4 Метод Гаусса с выбором главного элемента (оптимальный метод).
- •Применения метода Гаусса к вычислению определителей и обратных матриц.
- •Лекция № 5 Итерационные методы решения систем линейных алгебраических уравнений.
- •Лекция № 6 Метод Зейделя (модификация метода итераций).
- •Тогда условие окончания итерационного процесса Зейделя будет иметь вид:
- •Лекция № 7 Методы решения нелинейных уравнений и систем нелинейных уравнений.
- •1. Метод деления отрезка пополам (метод бисекций или дихотомия).
- •Метод хорд (метод линейной интерполяции).
- •3. Метод Ньютона (метод касательных или метод линеаризации).
- •4. Метод итераций (задача о неподвижной точке).
- •Оценка погрешности приближений:
- •Лекция № 8
- •1. Метод итераций для системы двух уравнений.
- •2. Метод Ньютона для системы двух уравнений.
- •Лекция №9 Алгебраическая проблема собственных значений.
- •Лекция № 10 Приближение функций и их производных.
- •Постановка задачи приближения функций.
- •2. Оценка погрешности полиномиальной интерполяции.
- •Лекция № 11 Интерполяционный многочлен Ньютона с конечными разностями.
- •Лекция № 12 Метод наименьших квадратов и наилучшие среднеквадратические приближения.
- •О нормальной системе мнк при полиномиальной аппроксимации.
- •Лекция №13 Сплайн интерполяция
- •Лекция № 15
- •Метод Эйлера – разные подходы к построению.
- •Методы Рунге – Кутта.
- •Лекция № 16
- •Лекция № 17 Разностные схемы для уравнений параболического типа.
- •Лекция №18
- •Лекция № 19 Разностные схемы для уравнений эллиптического типа.
Методы Рунге – Кутта.
В процессе вычислений фиксированы некоторые числа:
![]() 0<j<i
0<j<i![]() q;
q;
Последовательно получаем:
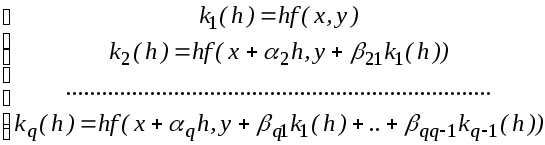
и
полагаем
![]()
Рассмотрим
вопрос о выборе параметров
![]()
Обозначим
![]() - погрешность на шаге.
- погрешность на шаге.
Если
f(x,y)-гладкая
функция своих аргументов, то
![]() тоже гладкие функции параметраh.
тоже гладкие функции параметраh.
Пусть
существуют производные
![]() а
а![]() выбраны так что
выбраны так что![]()
Кроме
того, предположим, что существует
![]() ,
для которой
,
для которой![]() .
.
Согласно формуле Тейлора выполняется равенство:
![]() ,
,
где
0<![]() <1
(15)
<1
(15)
Величина
![]() (h)-называется
погрешностью метода на шаге, а s-порядок
погрешности метода.
(h)-называется
погрешностью метода на шаге, а s-порядок
погрешности метода.
1. При q=1 имеем:
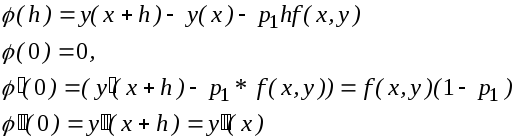
Равенство
![]() выполняется для всех гладких функцийf(x,y)
только при
выполняется для всех гладких функцийf(x,y)
только при
![]() .
.
Этому
значению
![]() соответствует метод Эйлера. Для
погрешности этого метода на шаге,
согласно (15) получаем выражение:
соответствует метод Эйлера. Для
погрешности этого метода на шаге,
согласно (15) получаем выражение:![]() .
.
Таким образом, s=1. Это метод первого порядка точности.
2. Рассмотрим q=2:
![]() где
где
![]() .
.
Вычисляем
производные
![]() ,
находим:
,
находим:
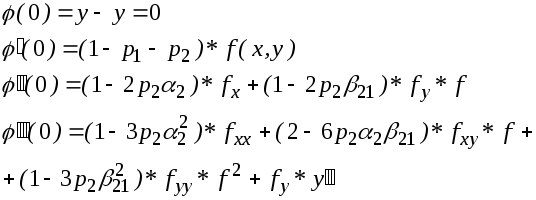
Соотношение
![]() ,
если
,
если![]()
![]() ,
если
,
если
![]()
Таким
образом,
![]() при всех
при всех![]() ,
если
,
если
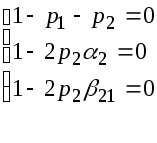
3 уравнения, 4 параметра. Задавая один из них произвольно, получим различные методы Рунге-Кутта с погрешностью второго порядка малости по h.
Например:
![]()
![]()
![]() ,
,
![]() ,
,![]() ,
что соответствует формулам (12) - метод
Эйлера пересчётом.
,
что соответствует формулам (12) - метод
Эйлера пересчётом.
![]()
![]()
![]() ,
,![]() ,
,![]() ,
что соответствует формулам (14) - метод
Эйлера с полуцелым шагом.
,
что соответствует формулам (14) - метод
Эйлера с полуцелым шагом.
Так
как
![]() ,
то нельзя построить формулы Рунге-Кутта
сq=3,
S=3;
,
то нельзя построить формулы Рунге-Кутта
сq=3,
S=3;
3. Рассмотрим q=4, S=4.
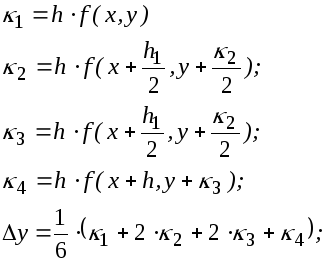 (16)
(16)
Один
из точных методов,
S=4,
![]() он
носит названиеметода
Рунге – Кутта.
он
носит названиеметода
Рунге – Кутта.
Численное решение дифференциальных уравнений высших порядков.
Рассмотрим однородное дифференциальное уравнение порядка (r)
![]()
Задача Коши: требуется найти частное решение, удовлетворяющее (r) начальным условиям:
![]()
Одним из способов численного решения начальных задач для дифференциальных уравнений высших порядков является их сведение к соответствующим задачам для систем уравнений первого порядка.
Заменой переменных сводим задачу к системе (r) уравнений 1-го порядка.
![]()
![]()
Например:
![]()
![]()
![]() начальные условия перепишутся в
виде
начальные условия перепишутся в
виде![]() т.
д.
т.
д.
Методы Рунге-Кутта легко распространяются на системы дифференциальных уравнений 1-го порядка.
Например:
рассмотрим систему
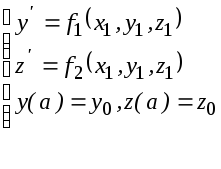
Приближённые
решения
![]() и
и![]() этой системы в точках
этой системы в точках![]() последовательно вычисляется по формулам:
последовательно вычисляется по формулам:
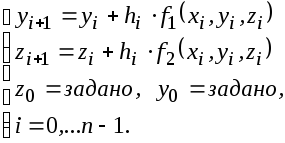 метод
Эйлера
метод
Эйлера
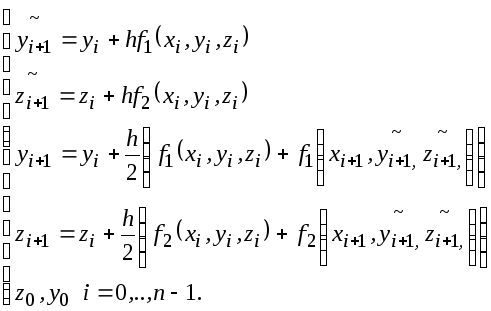
Метод Эйлера-Коши
Лекция № 16
Основные понятия теории разностных схем
Пусть на некотором отрезке D поставлена некоторая дифференциальная краевая задача.
![]() ,
(1)
,
(1)
L - заданный дифференциальный оператор, f - заданная правая часть.
Будем
предполагать, что решение u
задачи
(1) на отрезке
![]() существует.
существует.
На
отрезке D
конечное число точек,
![]() ,
,
Заменяем
u(x)
à
таблицей
![]() значений этого решения в
точках сетки
значений этого решения в
точках сетки![]() .
.
Предполагается,
что сетка
![]() зависит от параметраh>0.
зависит от параметраh>0.
Например,
можно положить h=1/N
, где N
- некоторое натуральное число, и принять
за сетку
![]() совокупность точек
совокупность точек![]() .
.
Искомая
сеточная функция
![]() в этом случае в точке сетки
в этом случае в точке сетки![]() принимает значения
принимает значения![]() ,
которое будем обозначать
,
которое будем обозначать![]() .
.
![]() .
(2)
.
(2)
Назовем ее разностной краевой задачей (разностной схемой).
Определение 1.
Будем
говорить, что решение
![]() разностной краевой задачи (2) при сгущении
сеткисходится
к решению u
дифференциальной
краевой задачи (1), если
разностной краевой задачи (2) при сгущении
сеткисходится
к решению u
дифференциальной
краевой задачи (1), если
![]() .
.
Если, сверх того, выполнено неравенство
![]() (3)
(3)
где С>0, k>o – некоторые постоянные, не зависящие от h, то будем говорить, что имеет место сходимость порядка hk или что разностная схема имеет k -й порядок точности.
В
этом определении
![]() - проекция точного решения задачи (1) на
сетку (
- проекция точного решения задачи (1) на
сетку (![]() -
сеточная функция, компоненты которой
есть значения точного решения в
узлах
сетки).
-
сеточная функция, компоненты которой
есть значения точного решения в
узлах
сетки).
Предположим,
что разностная задача (2) имеет единственное
решение
![]() .
.
Если
бы при подстановке в левую часть (2)
вместо
![]() сеточной функции
сеточной функции![]() (проекции точного решения на сетку)
равенство (2) оказалось бы в точности
выполненным, то ввиду единственности
решения имело бы место равенство
(проекции точного решения на сетку)
равенство (2) оказалось бы в точности
выполненным, то ввиду единственности
решения имело бы место равенство![]() =
=![]() ,
идеальное с точки зрения сходимости.
,
идеальное с точки зрения сходимости.
Это
означало бы, что решение
![]() разностной задачи (2) совпадает с искомой
сеточной функцией
разностной задачи (2) совпадает с искомой
сеточной функцией![]() ,
которую мы условились считать точным
решением.
,
которую мы условились считать точным
решением.
Однако,
как правило, систему (2) не удается
выбрать так, чтобы
![]() в точности ей удовлетворяла.
в точности ей удовлетворяла.
При подстановке в уравнение (2) возникает некоторая невязка:
![]()
Если
эта невязка
![]() стремится к нулю при
стремится к нулю при![]() ,
так что
,
так что![]() удовлетворяет уравнению (2) все точнее,
то будем говорить:
удовлетворяет уравнению (2) все точнее,
то будем говорить:
Определение 2.
Будем говорить, что разностная схема (2) аппроксимирует исходную дифференциальную задачу (1) на решении u, если
![]()
Если, сверх того, имеет место неравенство
![]() (4)
(4)
где С>0, k>o – некоторые постоянные, не зависящие от h, то будем говорить, что имеет место аппроксимация порядка hk или порядка к относительно величины h.
В
случае аппроксимации можно считать,
что уравнение (3) которому удовлетворяет
![]() ,
получается из уравнения (2) путем
прибавления к правой части некоторой
малой (при маломh)
добавки
,
получается из уравнения (2) путем
прибавления к правой части некоторой
малой (при маломh)
добавки
![]() .
.
Следовательно,
если решение
![]() задачи (2)устойчиво
относительно возмущения правой
задачи (2)устойчиво
относительно возмущения правой
![]() ,
т.е. мало изменяется при малом изменении
правой части, то решение
,
т.е. мало изменяется при малом изменении
правой части, то решение![]() задачи (2) и решение
задачи (2) и решение![]() задачи (3) отличаются мало, так что изаппроксимации
задачи (3) отличаются мало, так что изаппроксимации
![]() при
при
![]() следуетсходимость
следуетсходимость
![]() ,
при
,
при
![]()
Определение 3.
Будем называть разностную схему (2) устойчивой, если существуют такие постоянные h0 и d0, что при любом h<h0 и любой сеточной функции eрÎFh, такой, что
![]() разностная
задача
разностная
задача
![]() ,
,
полученная из (2) добавление к правой части возмущения eh имеет место и имеет только одно решение zh, причем справедлива оценка
![]() , (5)
, (5)
где С1 – некоторая постоянная, не зависящая от h.
Последнее неравенство означает, что малое возмущение eh правой части разностной схемы (2) вызывает равномерно относительно h малое возмущение (zh-uh) решения uh .
Определение 4.
Будем
называть разностную схему (2) с линейным
оператором
Lh
устойчивой,
если при любой правой части fhÎFh
уравнение
![]() имеет единственное решениеuhÎUh,
причем
имеет единственное решениеuhÎUh,
причем
![]() (6)
(6)
где С – некоторая постоянная, не зависящая от h.
Можно показать, в случае линейности разностного оператора Lh определения устойчивости 3 и 4 равносильны.
Теорема 1 (теорема Лакса о сходимости).
Пусть разностная схема (2) аппроксимирует задачу (1) на решении u с порядком hk и устойчива.
Тогда
решение разностной задачи
![]() сходится к решению дифференциальной
задачи
сходится к решению дифференциальной
задачи![]() ,
причем имеет место оценка
,
причем имеет место оценка
![]() ,
,
где С – некоторая постоянная, не зависящая от h.
Эта теорема позволяет свести вопрос о важнейшей с практической точки зрения проблеме исследования сходимости к вопросу исследования аппроксимации и устойчивости.
Доказательство:
Положим
![]() и
и![]() .
Тогда определение устойчивости (5)
.
Тогда определение устойчивости (5)
![]() примет
вид, (привлекая условие (4))
примет
вид, (привлекая условие (4))
![]()
