Лекция №1

§ 1. Задача вычисления.

Обычно задачу вычисления величины y по известной величине x записывают, с учетом интересующих нас причинно-следственных связей, в виде

(1)

Где yÎY, xÎX - элементы соответствующих функциональных пространств (как правило линейные, нормированные полные). A – оператор (правило), реализующий вычисления.

В первую очередь нас будут интересовать корректно поставленные задачи вычисления.

Задача вычисления называется корректно поставленной, если для любых входных данных из некоторого класса решение задачи существует, единственно и устойчиво по входным данным (т.е. непрерывно зависит от входных данных задачи).

При этом в первую очередь анализируют вопрос о вносимых в решение погрешностях

Есть четыре основных источника погрешности результата вычислений: математическая модель; исходные данные задачи; приближенный метод и погрешность при реализации вычислений (в частности погрешность округления):

• d₁y-погрешность математической модели, связана с физическими допущениями при выборе математической модели и на анализе этой погрешности мы останавливаться не будем;

• d₂y - погрешность исходных данных, порождает неустранимую погрешность решения

• d₃y - погрешность метода. Выражение A(x) , вообще говоря, не может быть просто численно реализовано. Задачу заменяют близкой задачей

(1')

мы переходим к другим функциональным пространствам , элементы которых допускают сравнительно простую численную реализацию. Соответствующим образом меняется и отображение.

при этом естественно требовать, чтобы задача (1') была корректна, и чтобы решение `y было близко к решению y. величина

и представляет собой погрешность метода.

• d₄y - вычислительная погрешность. При численной реализации `y , которая по предположению возможна получают элемент , поскольку промежуточные результаты округлялись т.п. таким образом,вычислительная погрешность может быть записана в виде

полезно сразу же сформулировать некоторые эмпирические правила, которых придерживаются при реализации задачи вычисления:

1. при проведении вычислений нужно стремиться, чтобы погрешность метода d₃y была бы в несколько раз меньше неустранимой погрешности решения d₂y;

2. вычислительная погрешность d₄y должна быть существенно меньше всех остальных погрешностей решения, т.е. расчет нужно вести с таким количеством значащих цифр, чтобы погрешность округления была существенно меньше всех остальных погрешностей.

Рассмотрим пример, иллюстрирующий эти определения. Пусть необходимо вычислить интеграл , гдеF(x) задана таблично на [a, b]

Для получения приближенного решения можно поступить следующим образом: заменим на промежутке [a, b] функцию F(x) интерполяционным полиномом P_n(x) степени £ n, принимающим в точке x_i те же значения, что и F(x), (такой многочлен существует и единственен).

Вместо интеграла будем находить интеграл, вычисление которого не составляет труда. В этом случае общая (полная) погрешность будет складываться из 3^-х частей:

1. Погрешностей, порождаемых неточностями исходных данных (т.е. табличными значениями Y=F(x)) – неустранимая погрешность;

2. Погрешности, порождаемой заменой F(x) полиномом P_n(x) – погрешность метода;

3. Погрешности округлений при вычислении 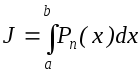-вычислительная погрешность.