
Раздел 1. Формальные грамматики
Лекция 1.
Тема лекции. Предварительные математические сведения. Основные понятия теории множеств. Операции над множествами. Свойства множеств. Произведение множеств. Отношения. Графы и деревья. Строки, формальные языки, операции над языками.
Для ознакомления с используемой в лекциях нотацией и правильного понимания излагаемого материала приводится краткий обзор понятий и положений из теории множеств и формальных языков, даются некоторые сведения о графах. Здесь также рассматриваются классификация формальных грамматик, отдельные их типы.
1.1 Обозначения и определения
1.1.1.Множества
Множество
- это набор несовпадающих объектов.
Объекты
обозначаются
своими
именами и называются элементами
множества.
Если множество содержит конечное число
элементов, то его можно задать простым
перечислением имен объектов. Например,
множество цветов можно определить
следующим
образом:
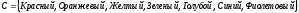
Множество
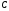 содержит семь элементов, которые
перечислены через запятую и заключены
в фигурные скобки. Порядок перечисления
элементов множества произвольный.
содержит семь элементов, которые
перечислены через запятую и заключены
в фигурные скобки. Порядок перечисления
элементов множества произвольный.
Если
объект
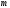 принадлежит
множеству
принадлежит
множеству
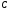 ,
то
,
то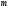 есть
элемент, что обозначается
есть
элемент, что обозначается
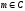 .
Если же
.
Если же
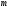 не является элементом множества
не является элементом множества
 ,
то это записывают в виде
,
то это записывают в виде
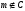 .
.
Например,
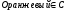 ,
а
,
а
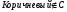 .
Задать множество простым перечислением
можно, когда оно содержит конечное число
элементов. Для задания бесконечных
множеств используется некоторое общее
свойство, которым должен обладать
объект, чтобы стать элементом данного
множества. Такое общее свойство записывают
в виде утверждения (предиката), содержащего
одну или несколько переменных. Предикат
может принимать одно из двух значений
- истина или ложь. В этом случае множество
состоит из тех элементов, для которых
предикат истинен. Выбирать предикат
необходимо осторожно, поскольку может
оказаться, что определяемое множество
не существует (парадокс Рассела). Примером
бесконечного множества может служить
множество
.
Задать множество простым перечислением
можно, когда оно содержит конечное число
элементов. Для задания бесконечных
множеств используется некоторое общее
свойство, которым должен обладать
объект, чтобы стать элементом данного
множества. Такое общее свойство записывают
в виде утверждения (предиката), содержащего
одну или несколько переменных. Предикат
может принимать одно из двух значений
- истина или ложь. В этом случае множество
состоит из тех элементов, для которых
предикат истинен. Выбирать предикат
необходимо осторожно, поскольку может
оказаться, что определяемое множество
не существует (парадокс Рассела). Примером
бесконечного множества может служить
множество
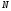 ,
содержащее целые числа.
,
содержащее целые числа.
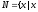 -простое
число
-простое
число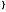
Переменная
 ,
принимает значения из заданного множества
и может быть целым числом.
,
принимает значения из заданного множества
и может быть целым числом.
Может
оказаться так, что множество не имеет
ни одного элемента (предикат принимает
значения ложь для всех значений
переменных). Такое множество называют
пустым множеством и обозначают
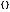 или
или
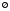 .
Множества могут быть элементами других
множеств, которые называют системами
множеств и обозначают
.
Множества могут быть элементами других
множеств, которые называют системами
множеств и обозначают
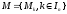 ,
где
,
где
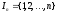
Говорят,
что множество
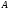 содержится
в множестве
содержится
в множестве
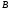 и пишут
и пишут
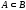 ,
если каждый элемент множества
,
если каждый элемент множества
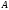 является элементом множества
является элементом множества
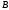 .
В этом случае множество
.
В этом случае множество
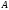 называют подмножеством множества
называют подмножеством множества
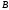 .
Если существует элемент
.
Если существует элемент
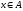 ,
который
не принадлежит
,
который
не принадлежит
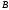
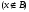 ,
то множество
,
то множество
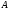 не является подмножеством множества
не является подмножеством множества
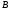 ,
что записывают в виде
,
что записывают в виде
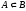 .
Например,
.
Например,
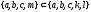 ,
в то время как
,
в то время как
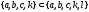
Следует
отметить, что пустое множество содержится
в любых других множествах
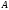 ,
,
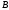 .
Два множества
.
Два множества
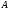 и
и
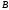 называются равными
называются равными
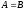 ,
если
,
если
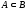 и
и
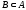 .
Например,
.
Например,
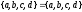 ,
в то время как
,
в то время как
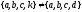
Таким
образом, множества
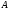 и
и
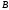 являются равными, если они совпадают
или другими словами содержат одни и те
же элементы.
являются равными, если они совпадают
или другими словами содержат одни и те
же элементы.
Из
множеств при помощи определенных
операций можно образовывать новые
множества. К основным операциям над
множествами относятся объединение
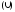 ,
пересечение
,
пересечение
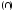 ,
вычитание
,
вычитание
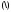 ,
дополнение
,
дополнение
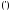 .
Предположим, что
.
Предположим, что
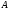 и
и
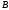 подмножества некоторого универсального
множества
подмножества некоторого универсального
множества
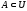 и
и
 .
Тогда основные операции можно определить
следующим образом:
.
Тогда основные операции можно определить
следующим образом:
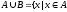 или
или
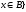 - объединение множеств, состоит из всех
элементов, принадлежащих, по крайней
мере одному из множеств
- объединение множеств, состоит из всех
элементов, принадлежащих, по крайней
мере одному из множеств
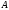 или
или
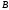 ;
;
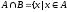 и
и
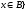 - пересечение множеств, состоит из всех
элементов, относящихся одновременно к
обоим множествам
- пересечение множеств, состоит из всех
элементов, относящихся одновременно к
обоим множествам
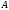 и
и
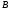 ;
;
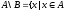 ,но
,но
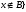 -
вычитание множеств, содержит все элементы
множества
-
вычитание множеств, содержит все элементы
множества
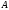 ,
которые не являются элементами множества
,
которые не являются элементами множества
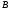 ;
;
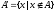 или
или
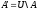 дополнение, охватывает все те элементы
множества
дополнение, охватывает все те элементы
множества
 ,
которые не являются
элементами
множества
,
которые не являются
элементами
множества
 .
.
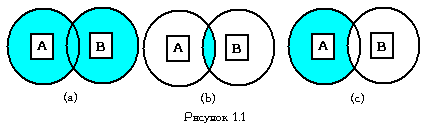
Графическое изображение выполнения операций над множествами представлено на рисунке 1.1 (а, b, с) в виде диаграмм Венна.
Рассмотрим
примеры выполнения операций для следующих
множеств
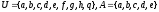 ,и
,и
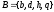 :
:
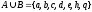
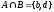
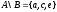
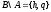
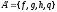
Для
любых множеств
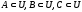 выполняются
следующие законы [2]:
выполняются
следующие законы [2]:
1) Ассоциативный закон:
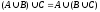
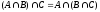
2) Коммутативный закон:
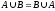
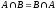
3) Закон о дополнении:
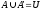
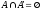
4) Закон идемпотенции:
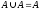
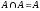
5) Закон эквивалентности:
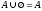
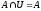
6) Закон существования пустого множества:
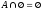
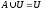
7) Закон инволюции:
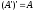
8) Закон Моргана:
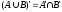
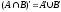
9) Дистрибутивный закон:
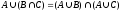
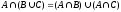
Поскольку
операции объединения и пересечения
множеств ассоциативны,
их можно применять для последовательности
множеств
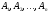 .
.
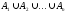 или
или
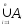
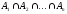 или
или
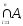
Особое
место среди операций над множествами
занимает прямое (декартово) произведение
множеств. Под произведением множеств
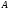 и
и
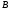 ,
обозначаемым через
,
обозначаемым через
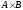 ,
понимают множество
,
понимают множество
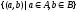 ,
состоящее из упорядоченных пар объектов.
Первый объект пары является элементом
множества
,
состоящее из упорядоченных пар объектов.
Первый объект пары является элементом
множества
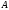 ,
второй - элементом множества
,
второй - элементом множества
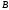 .
Рассмотрим пример
.
Рассмотрим пример
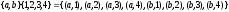
Отметим,
что в общем случае
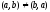 ,
но
,
но
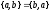 .
Аналогично можно определить произведение
трех и более множеств.
.
Аналогично можно определить произведение
трех и более множеств.
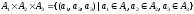
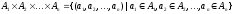
В
частности можно рассматривать произведение
 одинаковых
множеств
одинаковых
множеств
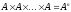
Между
элементами множеств могут существовать
определенные взаимосвязи или отношения.
Любое подмножество множества
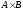 есть
отношение, при этом множество
есть
отношение, при этом множество
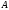 называют
областью определения, а множество
называют
областью определения, а множество
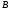 -
областью значений. Область определения
и область значений могут быть одним и
тем же множеством. Если
-
областью значений. Область определения
и область значений могут быть одним и
тем же множеством. Если
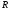 отношение
из
отношение
из
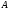 в
в
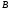 и
и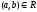 ,
то пишут
,
то пишут
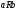 .
.
Отношение
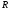 на множестве
на множестве
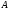 называют:
называют:
-
рефлексивным , если
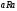 выполняется для всех
выполняется для всех
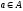 ;
; -
симметричным , если из
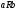 всегда следует
всегда следует
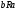 ;
; -
транзитивным , если из
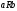 и
и
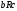 всегда следует
всегда следует
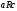 .
.
Рефлексивное, симметричное и транзитивное отношение называется отношением эквивалентности. Наряду с перечисленными выше отношениями важное значение имеет отношение, называемое отображением или функцией.
Функция
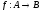 есть
отношение, определенное на множестве
есть
отношение, определенное на множестве
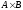 и представляющее собой множество пар
и представляющее собой множество пар
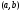 ,
где
,
где
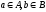 и
и
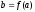 ,
причем, если
,
причем, если
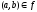 и
и
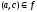 ,
то
,
то
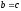 .
Такие функции называют однозначными.
Если функция определена на всех элементах
множества
.
Такие функции называют однозначными.
Если функция определена на всех элементах
множества
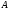 ,
то ее называют полной.
Полная функция будет взаимно
однозначной
, если из того, что
,
то ее называют полной.
Полная функция будет взаимно
однозначной
, если из того, что
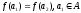 и
и
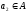 следует, что
следует, что
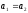 .
На рисунке 1.2 проиллюстрированы
перечисленные выше свойства функций.
Между множествами
.
На рисунке 1.2 проиллюстрированы
перечисленные выше свойства функций.
Между множествами
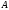 и
и
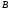 может быть установлено взаимно однозначное
соответствие, если существует полная
взаимно однозначная функция
может быть установлено взаимно однозначное
соответствие, если существует полная
взаимно однозначная функция
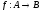 .
.









1.1.2 Графы и деревья.
Рассмотрим
множество
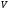 ,
соединенных некоторым образом точек.
Назовем
,
соединенных некоторым образом точек.
Назовем
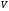 множеством вершин, а его элементы
множеством вершин, а его элементы
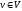 вершинами
[3]. Направленным
графом
вершинами
[3]. Направленным
графом
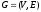 называется совокупность конечного
множества вершин и определенного на
этом множестве отношения
называется совокупность конечного
множества вершин и определенного на
этом множестве отношения
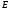 .
Направленный граф можно представить
графически следующим образом. Расположим
на листе бумаги все вершины множества
.
Направленный граф можно представить
графически следующим образом. Расположим
на листе бумаги все вершины множества
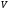 .
Каждую вершину изобразим в виде
окружности, внутри которой вписан
элемент множества
.
Каждую вершину изобразим в виде
окружности, внутри которой вписан
элемент множества
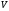 .
Две вершины
.
Две вершины
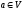 и
и
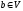 соединим отрезком линии, если существует
пара
соединим отрезком линии, если существует
пара
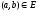 .
В этом случае будем говорить, что граф
.
В этом случае будем говорить, что граф
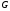 содержит ребро
содержит ребро
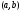 .
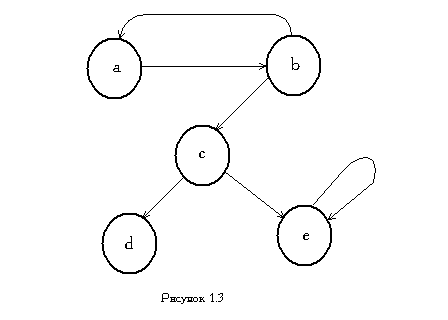
Например, на рис. 1.3 изображен граф
.
Например, на рис. 1.3 изображен граф
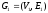 ,
где
,
где
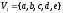 ,
,
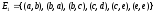 .
.
Если
в графе имеется некоторая последовательность
вершин
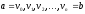 ,
где
,
где
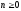 и
и
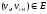 для
для
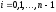 ,
говорят,
что в графе существует путь длиной
,
говорят,
что в графе существует путь длиной
 из вершины
из вершины
 в вершину
в вершину
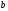 .
Для
.
Для
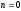
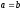 .
Граф
.
Граф
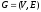 может
содержать подграфы вида
может
содержать подграфы вида
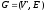 ,
если
,
если
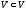 и
и
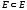 .
Два подграфа, не имеющие общих вершин,
называются раздельными подграфами.
.
Два подграфа, не имеющие общих вершин,
называются раздельными подграфами.
Для
нас представляет также интерес такая
разновидность
графа,
как дерево. Рекурсивное определение
дерева выглядит следующим образом.
Деревом
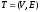 называют такой направленный граф,
который имеет либо одну единственную
вершину, называемую корнем
называют такой направленный граф,
который имеет либо одну единственную
вершину, называемую корнем
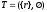 ,
либо совокупность корня, нескольких
раздельных подграфов-деревьев
,
либо совокупность корня, нескольких
раздельных подграфов-деревьев
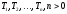 и
ребер от корня дерева
и
ребер от корня дерева
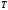 до вершин-корней деревьев
до вершин-корней деревьев
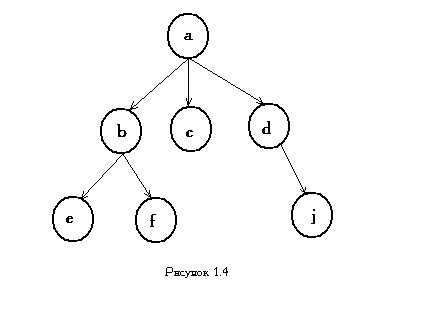
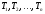 .На
рис. 1.4 представлен пример дерева. Обычно
дерево представляют в виде расположенного
вверху корня и направленных сверху вниз
ребер. В этом случае можно не указывать
направление ребер. Вершину дерева из
которой не выходит ни одного ребра
называют листом, остальные вершины -
внутренними вершинами дерева.
.На
рис. 1.4 представлен пример дерева. Обычно
дерево представляют в виде расположенного
вверху корня и направленных сверху вниз
ребер. В этом случае можно не указывать
направление ребер. Вершину дерева из
которой не выходит ни одного ребра
называют листом, остальные вершины -
внутренними вершинами дерева.

1.1.3. Строки.
В
данном курсе в основном рассматриваются
такие множества, элементами которых
являются символы, цепочки символов или
строки. Под строкой
всегда понимается некоторая
последовательность символов
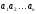 ,
каждый из которых принадлежит некоторому
конечному алфавиту
,
каждый из которых принадлежит некоторому
конечному алфавиту
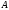 .
Например, строка
.
Например, строка
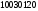 состоит из символов алфавита
состоит из символов алфавита
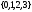 .
В дальнейшем для обозначения отдельных
символов будем использовать строчные
буквы
.
В дальнейшем для обозначения отдельных
символов будем использовать строчные
буквы
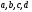 ,
а для обозначения строк - буквы
,
а для обозначения строк - буквы
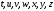 .
Строка, состоящая из
.
Строка, состоящая из
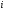 символов
символов
 ,
будет обозначаться
,
будет обозначаться
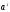 .
Длина произвольной строки
.
Длина произвольной строки
 представляет
собой число символов в строке и
обозначается
представляет
собой число символов в строке и
обозначается
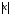 .
В приведенном выше примере
.
В приведенном выше примере
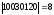 .
В общем случае существует пустая строка
.
В общем случае существует пустая строка
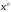 ,
которая имеет нулевую длину
,
которая имеет нулевую длину
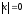 и обозначается
и обозначается
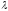 .
.
Формально
строки символов в алфавите
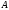 определяются следующим образом [1]:
определяются следующим образом [1]:
-
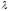 -
строка в
-
строка в
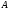 ;
; -
если
 - строка в
- строка в
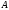 и
и
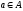 ,
то
,
то
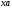 - строка в
- строка в
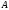 ;
; -
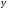 -
строка тогда и только тогда, когда она
является таковой в силу первых двух
положений.
-
строка тогда и только тогда, когда она
является таковой в силу первых двух
положений.
Над
строками можно выполнить ряд операций.
Если
 и
и
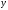 строки, то строка
строки, то строка
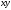 называется конкатенацией
(сцеплением или объединением)
называется конкатенацией
(сцеплением или объединением)
 и
и
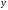 .
Например, если
.
Например, если
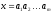 ,
а
,
а
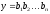 ,
тогда
,
тогда
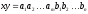 .
Отметим, что операция конкатенации
является ассоциативной операцией, но
не коммутативной, т.е.
.
Отметим, что операция конкатенации
является ассоциативной операцией, но
не коммутативной, т.е.
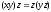 ,
но
,
но
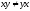 .
Для пустой строки справедливо следующее
утверждение
.
Для пустой строки справедливо следующее
утверждение
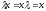 для любого
для любого
 .
Обращением строки
.
Обращением строки
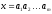 называется строка, записанная в обратном
порядке
называется строка, записанная в обратном
порядке
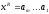 .
.
Пусть
 ,
,
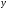 и
и
 произвольные строки в некотором алфавите
произвольные строки в некотором алфавите
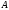 и строка
и строка
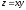 ,
тогда строка
,
тогда строка
 называется префиксом
строки
называется префиксом
строки
 ,
а строка
,
а строка
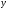 -
суффиксом
строки
-
суффиксом
строки
 .
Например, для приведенной выше строки
.
Например, для приведенной выше строки
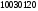 префиксом являются строки:
префиксом являются строки:
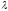 ,
,
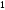 ,
,
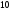 ,
,
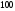 ,
,
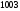 ,
,
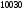 ,
,
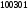 ,
,
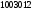 ,
,
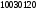 ,
а суффиксом строки:
,
а суффиксом строки:
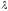 ,
,
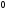 ,
,
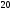 ,
,
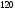 ,
,
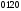 ,
,
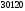 ,
,
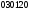 ,
,
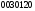 ,
,
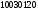 .
.
1.1.4. Формальные языки.
Обозначим
через
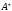 множество определенных над алфавитом
множество определенных над алфавитом
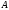 строк. Например, для
строк. Например, для
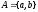
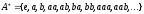
Множество
всех строк в
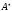 за исключением
за исключением
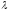 обозначается
обозначается
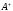 .
Таким образом
.
Таким образом
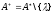 .
.
Формальным
языком
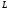 над алфавитом
над алфавитом
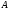 называется произвольное подмножество
множества
называется произвольное подмножество
множества
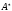 .
Пусть
.
Пусть
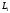 и
и
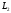 - два формальных языка, тогда их
конкатенация (объединение)
- два формальных языка, тогда их
конкатенация (объединение)
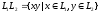 также является формальным языком.
Например, для языков
также является формальным языком.
Например, для языков
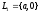 и
и
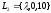 ,
,
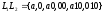 .
Конкатенация формального языка
.
Конкатенация формального языка
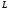 с самим собой записывается в виде
с самим собой записывается в виде
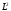 .
В общем случае это выглядит так
.
В общем случае это выглядит так
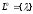 ,
,
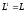 ,
,
 для
для
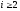 .
Тогда
.
Тогда
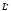 можно определить как
можно определить как
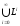 ,
а
,
а
