Лекции / Лекции (ЭТМО-2, Завьялова) / Лекц 6

Лекция 6.

$9. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.

Пусть Х – случайная величина с функцией распределения F(x). Если функция распределения дифференцируема, то ее производная F(x) = f(x) называется плотностью распределения, а сама случайная величина Х – непрерывно распределенной случайной величиной.

Отсюда следует, что функция распределения непрерывной случайной величины является первообразной от плотности распределения:

Утверждение 8. Cлучайная величина Х принимает значения из отрезка [x₁, x₂] c вероятностью F(x₂) – F(x₁).

Доказательство. P{x₁  X  x₂} = F(x₂) – Р(Х < x₁) = F(x₂) – F(х₁) (Т.к. F(х) непрерывна, для любого  > 0 существует  > 0 такая, что т.е. Поскольку для любого  > 0 то для любого  > 0 и значит, ). 

Cледствие. Вероятность того, что случайная величина Х принимает значения из отрезка [а, b] равна интегралу по этому отрезку от плотности распределения случайной величины Х.

Утверждение 9. При непрерывном распределении вероятности каждой отдельной точке соответствует вероятность 0, а отрезку [а, b] cоответствует та же вероятность, что и интервалу (a, b).

Доказательство. P(X = x) = P(x  X  x) = F(x) – F(x) = 0.

P(a  X  b) = P{a  X  b} – Р{Х = а} – Р{Х = b} = P{a < X < b}.

Свойства плотности распределения вытекают из свойств функции распределения ($2, Утверждения 1,3):

1) поскольку функция распределения не убывает, ее производная неотрицательна: f(x)  0;

2) интеграл от плотности по всей числовой прямой равен 1:

Замечание. Будем также рассматривать непрерывные случайные величины, сосредоточенные на интервале (a,b). Это такие случайные величины, у которых фукция распределения F(x) непрерывна, равна 0 при х  а, равна 1 при x  b, а на интервале (a, b) - дифференцируема. Плотность распределения таких случайных величин полагают равной 0 вне интервала (a, b) и F(x) на (a, b).

$10. ХАРАКТЕРИСТИКИ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН.

Математическим ожиданием непрерывной случайной величины Х называется если интеграл существует.

Моментом k-ого порядка, k = 1, 2, 3,…, непрерывной случайной величины Х называется математическое ожидание случайной величины Х^k:

Центральным моментом k-ого порядка непрерывной случайной ведичины Х

называется математическое ожидание случайной величины (Х – МХ)^k .

Как и для дискретных случайных величин дисперсия DХ непрерывной случайной величины Х - это второй центральный момент, среднее квадратическое отклонение, коэффициент асимметрии а_Х   = .

$11. ПРИМЕРЫ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН.

Пример 16. Равномерное распределение. Пусть на интервал (а, b) действительной прямой наугад бросают точку. Cлучайная величина Х – координата этой точки. Вероятность попадания точки на заданный интервал (х₁, x₂) из (a,b) 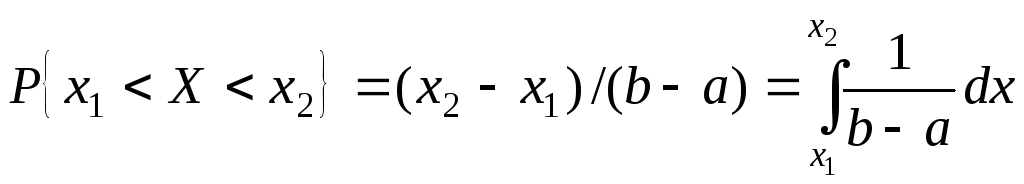. Поэтому плотность распределения

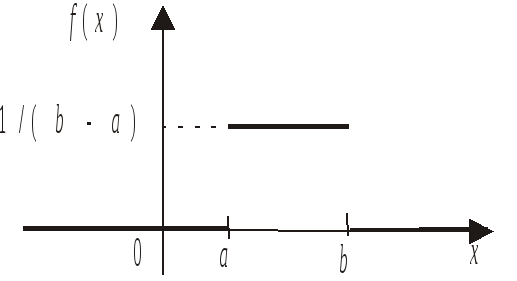
Такое распределение вероятностей называется равномерным на интервале (a, b).

Ф

ункция распределения равномерного закона

DX = M (X²) –(MX)² = 

В примере 1 из пятого параграфа первой главы время прихода пассажира на платформу метрополитена имеет равномерное распределение в интервале (0, 4). 

П

ример 17. Показательное распределение. Cлучайная величина Х имеет показательное распределение, если плотность распределения

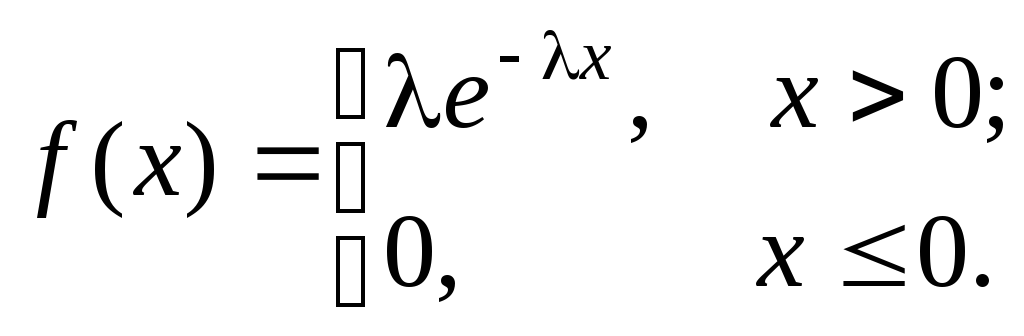
Функция распределения

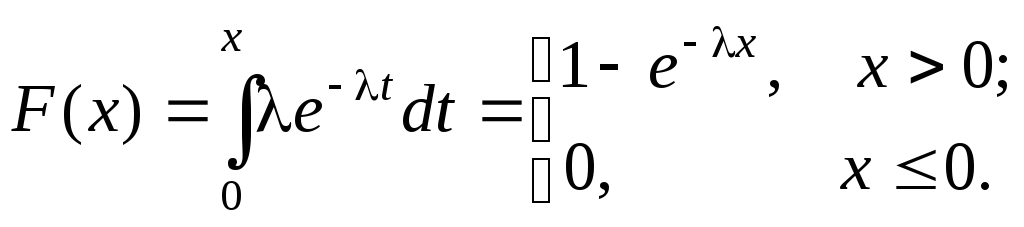
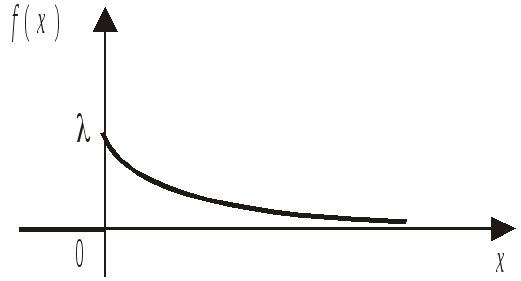
Показательное распределение часто имеют периоды ожидания или продолжительности “жизни” элементов (например, время до прихода автобуса или время “жизни” электрической лампочки). Показательное распределение обладает свойством отсутствия последействия: каков бы ни был настоящий “возраст” элемента, оставшееся время “жизни” не зависит от прошлого и имеет то же самое распределение, что и само время “жизни”. Отсутствие последействия присуще только показательному распределению. 

П

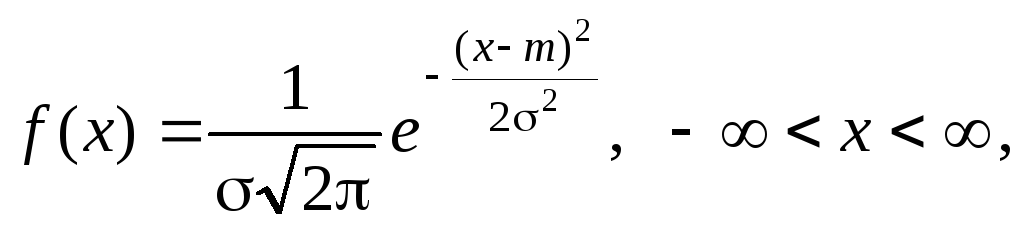ример 18. Нормальное распределение. Непрерывное распределение с плотностью называется нормальным распределением .

Графиком плотности является

так называемая гауссова кривая.

Она симметрична относительно параметра m.

Параметр m также совпадает с математическим ожиданием нормально распределенной случайной величины, т.к. .

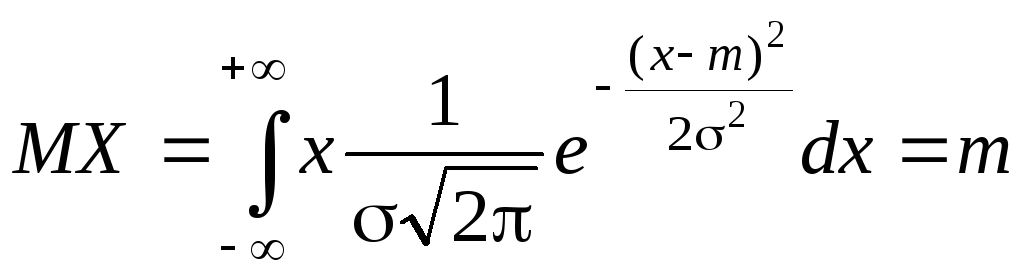Cо вторым параметром  совпадает среднее квадратическое отклонение, поскольку .

В силу симметричности плотности нормального распределения относительно математического ожидания любой центральный момент нечетного порядка равен нулю. следовательно, коэффициент асимметрии нормального распределения

а_Х  = 

Для нормального распределения отношение . равно 3. Это отношение принимают за эталон для всех распределений и величину называют коэффициентом эксцесса. Коэффициент эксцесса характеризует островершинность распределения. Для нормального закона он равен нулю. Для более островершинных распределений коэффициент эксцесса положительный, для менее островершинных - отрицательный.

Нормальное распределение с параметрами m = 0 и  = 1 называется стандартным нормальным распределением. Плотность стандартного нормального распределения

График плотности симметричен относительно нуля. 

$12. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ НОРМАЛЬНОГО ЗАКОНА.

Функция распределения стандартного нормального закона равняется интегралу

Но этот интеграл не берется в элементарных функциях. Функция F(x) относится к так называемым специальным функциям. Она обозначается Ф(x), значения ее можно найти в таблицах справочника по специальным функциям.

В силу симметричности стандартной нормальной плотности относительно нуля

Ф(–x) = 1 – Ф(x), – < x < .

Утверждение 10. Функция распределения F(x) нормального закона с параметрами m и  связана c функцией распределения стандартного нормального закона следующим соотношением

.

Доказательство.

.

Пример 19. Письменная работа на тестовых экзаменах оценивается в процентах. Cредняя оценка оказалась равной 50. Восемь десятых от общего количества абитуриентов получили оценки от 30 до 70. Cчитая, что оценка за письменную работу X имеет нормальное распределение, найдем среднее квадратическое отклонение этого распределения.

Р (30  X  70) = F(70) – F(30) = Ф((70-50)/) – Ф((30 – 50)/) = Ф(20/) –  – Ф(–20/) = 2*Ф(20/) – 1 = 0,8. Отсюда Ф(20/) = 0,9. Из таблицы функции распределения стандартного нормального закона следует, что 20/ = 1,28 и   15,625. 

5