Правило Ленца

Направление индукционного тока в контуре определяется правилом Ленца: индукционный ток направлен так, чтобы своим магнитным полем противодействовать изменению магнитного потока, которым он вызван. С учетом правила Ленца закон электромагнитной индукции записывают в виде .

Знак «минус» в этой формуле как раз и свидетельствует о «противодействии», оказываемом индукционным током его изменению.

25

• Явление самоиндукции. Индуктивность. Энергия магнитного поля.

Самоиндукция — это явление возникновения ЭДС индукции в проводящем контуре при изменении протекающего через контур тока.

При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность, ограниченную этим контуром. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.

Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока :

.

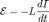Коэффициент пропорциональности  называется коэффициентом самоиндукции или индуктивностью контура (катушки).

Индукти́вность  — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность, краем которой является этот контур.

В формуле

 — магнитный поток,  — ток в контуре,  — индуктивность.

Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока:

.

Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.

Из закона сохранения энергии следует, что вся энергия, запасенная в катушке, выделится в виде джоулева тепла. Если обозначить через R полное сопротивление цепи, то за время Δt выделится количество теплоты ΔQ = I2 R Δt.

Ток в цепи равен 

Выражение для ΔQ можно записать в виде 

ΔQ = –L I ΔI = –Φ (I) ΔI.

В этом выражении ΔI < 0; ток в цепи постепенно убывает от первоначального значения I0 до нуля. Полное количество теплоты, выделившейся в цепи, можно получить, выполнив операцию интегрирования в пределах от I0 до 0. Это дает 

26

• Уравнения Максвелла для электромагнитного поля. Ток смещения.

Ток смещения или абсорбционный ток — величина, прямо пропорциональная скорости изменения электрической индукции

27

• Плоская электромагнитная волна. Волновое уравнение и его решение. Свойства волн. Скорость света.

Волна называется плоской, если поверхности равных фаз представляют собой плоскость, т.е. в плоской электромагнитной волне векторы  и  расположены в плоскости хода, перпендикулярно направлению распространения волны.