
Параграф 5_Свойства равн_сх_фп и рядов
.doc§ 5. Свойства равномерно сходящихся функциональных последовательностей и функциональных рядов
-
Предельный переход в функциональных последовательностях и функциональных рядах. Непрерывность и равномерная сходимость.
Теорема 1. ( о предельном переходе в функциональных последовательностях).
Пусть
fn
(x)
: X
®
R
,
![]() ,
,
![]() .
E
множество сходимости функциональной
последовательности
.
E
множество сходимости функциональной
последовательности
![]() N
. E
Ì
X
и пусть x
E.
N
. E
Ì
X
и пусть x
E.
Если функциональная
последовательность
![]() сходится
равномерно
к функции f(х)
на множестве E
при
сходится
равномерно
к функции f(х)
на множестве E
при
![]() и существует
и существует
![]() для любого
для любого
![]() N,
тогда
существуют
N,
тогда
существуют
![]() и
и
![]() .
.
![]() .
(1)
.
(1)
Следствие 1.
Пусть при
![]() fn
(x)
⇉
f(х)
на множестве E,
содержащем точку x
, и
fn
(x)
⇉
f(х)
на множестве E,
содержащем точку x
, и
функции fn
(x)
,
![]() N,
непрерывны
в точке
x
, тогда
предельная функция f(х)
непрерывна
в точке x
.
N,
непрерывны
в точке
x
, тогда
предельная функция f(х)
непрерывна
в точке x
.
Следствие 2.
Пусть при
![]() fn
(x)
⇉
f(х)
на множестве E
и
fn
(x)
⇉
f(х)
на множестве E
и
функции fn
(x)
,
![]() N,
непрерывны
на множестве
E
, тогда
предельная
функция f(х)
непрерывна
на множестве
E
.
N,
непрерывны
на множестве
E
, тогда
предельная
функция f(х)
непрерывна
на множестве
E
.
Равномерная сходимость функциональной последовательности – достаточное условие непрерывности предельной функции . Непрерывность предельной функции необходимое условие равномерной сходимости функциональной последовательности.
Теорема 1′. ( о предельном переходе в функциональных рядах).
Если при
![]()
![]() ⇉
S(х)
на множестве E,
содержащем точку x
, и
⇉
S(х)
на множестве E,
содержащем точку x
, и
при любом
![]() N
существует
N
существует
![]() ,
тогда числовой
ряд
,
тогда числовой
ряд
![]() сходится и имеет место равенство
сходится и имеет место равенство
![]() . (2)
. (2)
В равномерно сходящемся ряде можно переходить к пределу. Предел суммы (бесконечной) равен сумме (бесконечной ) пределов.
Следствие 3.
Пусть при
![]()
![]() ⇉
S
(х)
на множестве E
и
функции fn
(x)
,
⇉
S
(х)
на множестве E
и
функции fn
(x)
,
![]() N,
непрерывны
на множестве E
, тогда
функция S
(х)
непрерывна на
множестве E
.
N,
непрерывны
на множестве E
, тогда
функция S
(х)
непрерывна на
множестве E
.
Равномерная сходимость функционального ряда – достаточное условие непрерывности суммы функционального ряда . Непрерывность суммы функционального ряда необходимое условие равномерной сходимости функционального ряда.
Теорема 2. ( теорема Ди′ни - достаточное условие равномерной сходимости функциональных последовательностей ) ( Улисс Дини (1845-1918) – итальянский математик) .
Если
последовательность непрерывных функций
fn
(x),
заданных на отрезке
[ a,
b]
, не убывает
и сходится
поточечно
к непрерывной
функции
f(х),
то функциональная
последовательность
![]() сходится
равномерно к
функции f(х).
сходится
равномерно к
функции f(х).
Теорема 2′.
( теорема Дини - достаточное условие
равномерной сходимости функциональных
рядов ) Если
сумма
ряда S
(х)
=
![]() с неотрицательными
непрерывными
функциями
fn
(x)
непрерывна
на отрезке [ a,
b]
, то этот ряд
сходится
равномерно к
функции S
(х)
на
отрезке [ a,
b].
с неотрицательными
непрерывными
функциями
fn
(x)
непрерывна
на отрезке [ a,
b]
, то этот ряд
сходится
равномерно к
функции S
(х)
на
отрезке [ a,
b].
-
Предельный переход под знаком интеграла. Почленное интегрирование функциональных последовательностей и функциональных рядов.
Теорема 31. (интегрирование функциональных последовательностей )
Если последовательность
непрерывных
функций
fn
(x)
сходится
равномерно
на отрезке [ a,
b]
к функции f(х)
при
![]() , то функциональная
последовательность интегралов сходится
равномерно
к
, то функциональная
последовательность интегралов сходится
равномерно
к
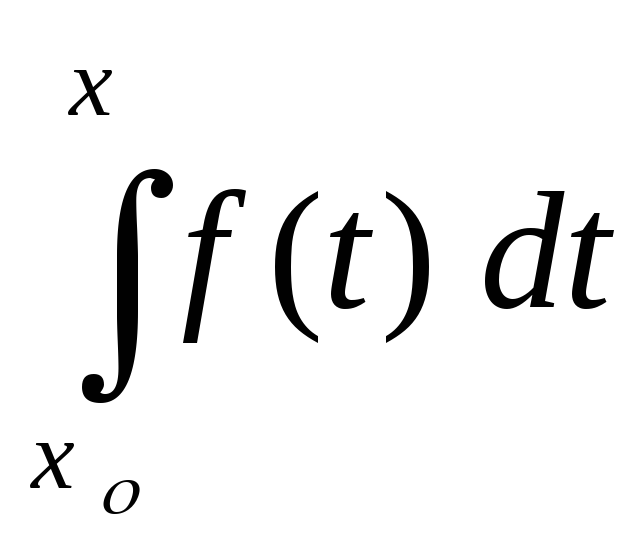 при
при
![]() для любых
x
, x
[ a,
b].
для любых
x
, x
[ a,
b].
(
![]() ⇉
f(х)
при
⇉
f(х)
при
![]() на отрезке
[ a,
b]
)
на отрезке
[ a,
b]
)
(
 ⇉
⇉ при
при
![]() для любых
x
, x
[ a,
b]
), т.е.
для любых
x
, x
[ a,
b]
), т.е.
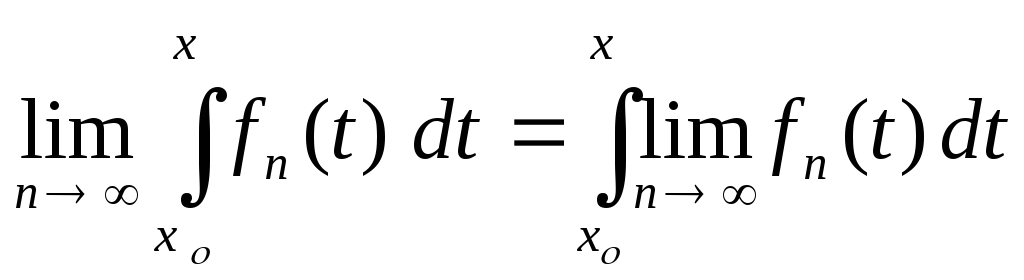 ,
(3)
,
(3)
операции взятия предела и интеграла перестановочны.
Теорема 32. (интегрирование функциональных последовательностей )
Если последовательность
функций fn
(x),
интегрируемых
по Риману на отрезке [
a,
b],
сходится
равномерно
на отрезке [ a,
b]
к функции f(х)
при
![]() , то функциональная
последовательность интегралов
сходится
равномерно
к
, то функциональная
последовательность интегралов
сходится
равномерно
к
 при
при
![]() на отрезке
[ a,
b]
для любых x
, x
[ a,
b]
и верно равенство
на отрезке
[ a,
b]
для любых x
, x
[ a,
b]
и верно равенство
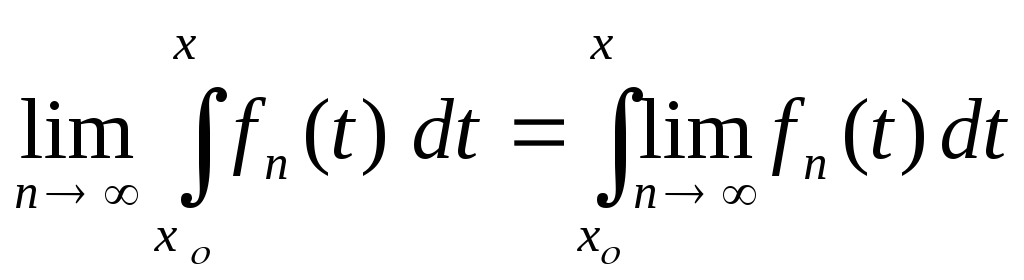 .
(3)
.
(3)
Теорема 32′. (интегрирование функциональных рядов )
Сумма
S
(х)
равномерно
сходящегося
на отрезке [
a,
b]
ряда
![]() ,
состоящего из интегрируемых
по Риману на отрезке [ a,
b]
функций ,
интегрируема по Риману
на отрезке [ a,
b].
,
состоящего из интегрируемых
по Риману на отрезке [ a,
b]
функций ,
интегрируема по Риману
на отрезке [ a,
b].
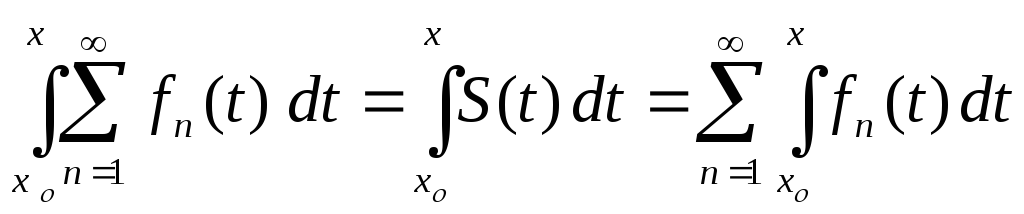 . (4)
. (4)
Равномерно сходящиеся ряды можно почленно интегрировать.
Интеграл от суммы ( бесконечной) функций равен сумме (бесконечной) интегралов.
-
Предельный переход под знаком производной. Почленное дифференцирование функциональных последовательностей и функциональных рядов.
Теорема 41. (дифференцирование функциональных последовательностей )
Если последовательность
непрерывно
дифференцируемых
функций f
n
(x)
сходится
поточечно
на отрезке [
a,
b]
к функции f
(х)
при
![]() , а
последовательность производных f
n
̉̍
(x)
сходится
на отрезке [ a,
b]
к функции φ
(х)
при
, а
последовательность производных f
n
̉̍
(x)
сходится
на отрезке [ a,
b]
к функции φ
(х)
при
![]() , то функция
f
(х)
дифференцируема на отрезке [
a,
b]
и
, то функция
f
(х)
дифференцируема на отрезке [
a,
b]
и
![]() ,
(5)
,
(5)
т.е. допустим предельный переход под знаком производной.
Теорема 42. (дифференцирование функциональных последовательностей )
Если каждая из
функций последовательности
![]() имеет производную на
отрезке [ a,
b]
и сходится
хотя бы в одной точке
x
[ a,
b]
к функции f(х)
при
имеет производную на
отрезке [ a,
b]
и сходится
хотя бы в одной точке
x
[ a,
b]
к функции f(х)
при
![]() , а функциональная
последовательность производных
, а функциональная
последовательность производных![]() сходится
равномерно
к φ
(х)
при
сходится
равномерно
к φ
(х)
при
![]() на отрезке
[ a,
b]
, то функция f
(х)
дифференцируема на отрезке [
a,
b]
и
на отрезке
[ a,
b]
, то функция f
(х)
дифференцируема на отрезке [
a,
b]
и
![]() .
(5)
.
(5)
