Лекция 05. Гиперболические функции

Лекция 5. Гиперболические функции.

5.1. Гиперболические косинус и синус.

Гиперболический косинус – это функция, зависящая от переменной х: .

Обозначение ch – сокращение латинских слов соsinus hyperbolicus.

Cвязь с показательной функцией следующая:

. (5.1)

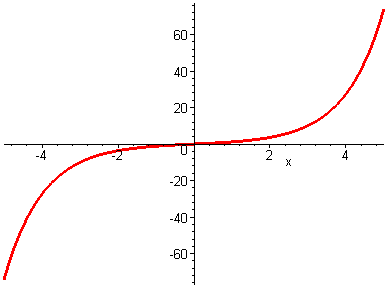
График функции изображён на рис. 5.1.

Функция принимает значения, не меньшие единицы ().

Рис. 5.1.

Гиперболический синус – это функция, зависящая от переменной х: .

Обозначение sh – сокращение латинских слов sinus hyperbolicus.

Cвязь с показательной функцией следующая:

. (5.2)

График функции изображён на рис. 5.2.

Функция принимает все возможные значения.

Рис. 5.2.

5.2. Гиперболические тангенс и котангенс.

Гиперболическим тангенсом и котангенсом называются соответственно функции

, (5.3)

. (5.4)

Значения функции содержатся между –1 и +1, значения больше +1 при и меньше –1 при . Прямые и служат горизонтальными асимптотами для обеих функций и .

График функции изображён на рис. 5.3, – на рис. 5.4.

Рис. 5.3.	Рис. 5.4.

5.3. Формулы для гиперболических функций.

Гиперболические функции связаны отношениями

, , , .

Для гиперболических функций доказываются формулы, аналогичные тригонометрическим. Так, например,

,

,

.

Эти формулы вытекают из формул (5.1)–(5.4).

Для каждой тригонометрической формулы, не содержащей постоянных величин под знаками тригонометрических функций, есть аналогичное соотношение между гиперболическими функциями. Для получения этих соотношений нужно в тригонометрических формулах заменить всюду на , а на , мнимости устранятся сами собой.

 Пример 5.1. Из тригонометрической формулы c помощью указанной замены получаем .

Разделив обе части равенства на i, получим . 

 Пример 5.2. Из формулы получаем .

Так как , то . 

5.4. Обратные гиперболические функции.

Для гиперболических функций , , , существуют обратные гиперболические функции:

– гиперболический ареасинус (рис. 5.5),

– гиперболический ареакосинус (рис. 5.6),

– гиперболический ареатангенс (рис. 5.5),

– гиперболический ареакотангенс (рис. 5.7).

Слово area в переводе с латинского означает площадь, что и объясняет приведённые названия.

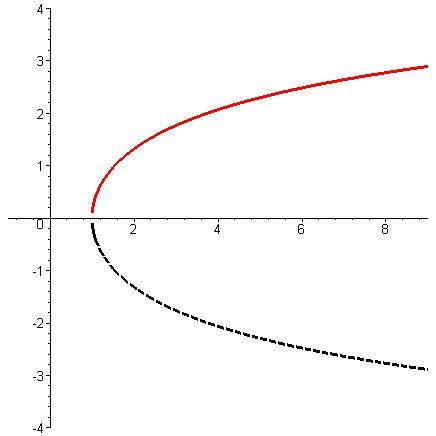
Функция однозначно определена на всей числовой оси. Через элементарные функции она выражается так: .

Функция однозначна, она определена в промежутке . Через элементарные функции выражается так: , где .

Рис. 5.5.

Функция определена на интервале и двузначна, значения её равны по абсолютной величине и отличаются знаком. Обычно рассматриваются лишь положительные значения; соответствующая ветвь графика (главная ветвь) расположена выше оси Ох. При этом условии функция становится однозначной, через элементарные функции выражается так: , .

Рис. 5.6.

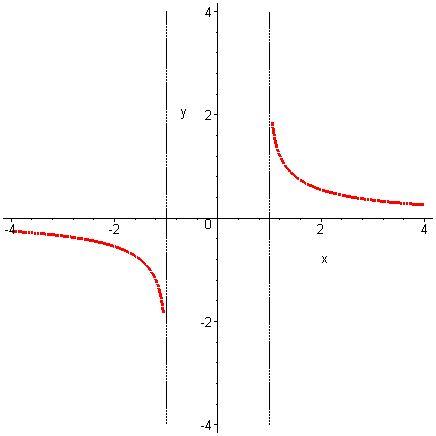
Функция определена вне промежутка . Прямые служат асимптотами для кривой . Выразим через элементарные функции:

, где

Рис. 5.7.

25