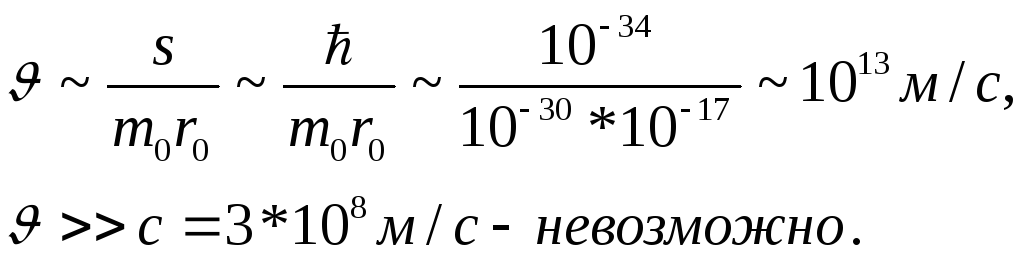§ 6. Круговые токи в атоме и магнитный момент орбитального движения электрона.

Состояние электрона в атоме водорода описывается волновой функцией вида:

.

Зная волновую функцию можно вычислить плотность тока вероятности:

.

Так как радиальная функция и полиномыявляются действительными функциями, то очевидно

Вывод: в стационарном состоянии атома проекции токов на радиус и медиан равен нулю, и токи текут вдоль широких кругов вокруг оси z.

Тогда .

Рассмотрим круговой проводник с током силой I, охватывающую поверхность площадью S:

Магнитный момент: . Разобьем весь объем атома на тонкие трубки тока сечением, текущей вокруг осиz. Величина тока в трубке:

Так как все магнитные моменты всех трубок тока направлены вдоль оси z, тогда полный магнитный момент будет равен:

-магнитон Бора.

, .

Запишем последнее выражение в векторном виде, учитывая, что :

.

Учитывая произвольности выбора оси z, последнее равенство можно записать в векторном виде: .

Аналогичная формула имеет место и в классической физике, однако в квантовой физике векторы , принимают дискретные значения:

l=0,1,2,...

.

§ 7. Понятие спина электрона.

Состояние атома описывается тремя квантовыми числами главным n, орбитальнымlи магнитнымml. Однако для описания всех свойств атома необходимо вводить четвертое квантовое число, называемым спином. Впервые идея была выдвинута Паулем. Представление спина как вращение и сам термин спин выдвинули Уленбек и Гаудсмит (1925г.). Строгую теорию спина можно построить лишь в рамках релятивисткой квантовой механики, основанной на уравнении Дирака. Из-за отсуствия траектории электрона невозможно определить явление вращения самого электрона. Однако наличие собственного механического момента спина должно приводить к появлению спинового магнитного момента, то есть- собственный механический момент (спин):. Электрон должен обладать спиновым магнитным моментом:. Будем предполагать, чтоа проекция на осьz.

ms=-s...+s.

Отсюда следует, должно принимать (2s+1) дискретное значение.

. То что электрон обладает спином говорят три эксперимента:

1. Опыт Штерна-Герлаха.

2. Дублетная структура спектра паров щелочных металлов.

3. Опыт Эйштейна-де Газа.

Суть первого опыта состояла в пропускании атомов серебра через

неоднородное магнитное поле. Брали откаченный баллон, ставилась диофрагмма:

В этом опыте были использованы атомы серебра по следующим соображениям: во-первых, атом является электронейтральной системой, на которую не действует сила Лоренца; во-вторых, серебро имеет единственный внешний валентный электрон находящийся в постоянном S-состоянии,l=0, . Следовательно, у этого атома отсуствует орбитальный момент, значит .

Bx=0,By=0,Bz=B(z) направление вдоль осиz.

, если попадает в поле.

На атом действует сила: .

Таким образом, на атом действует сила пропорциональна спиновым магнитным моментам, но так как спин принимает (2s+1) дискретных проекций, то пучок атомов пропущенных через неоднородное магнитное поле должен расщепляться на (2s+1) компоненту и на экране должно наблюдаться (2s+1) посеребренное пятно. Из этого опыта следует электрон всегда закручен:

В этом опыте измеряя расстояние между крайними точками можно измерить силу, действующую на атомы и для заданного градиента поля можно измерить .

, следовательно, .

.

Отсюда следует, что отношение магнитного момента к механическому в двое больше, чем для орбитального момента.

Во втором эксперименте, рассматривают атом натрия Na.

При возбуждении атома Naвалентный электрон переходит в 3pсостояние, а затем возвращается вниз 3sв основное состояние и излучает квант света.

Это явление появление двух желтых линий можно объяснить, 3sявляется одиночным уровнем, а 3pдвойным. Дальнейший анализ показал, что всеsдолжны быть одиночными, а всеp,d,fдолжны быть двойными. Указанное расщепление можно объяснить, введя дополнительное, спинно-орбитальное взаимодействие. Рассматривая качественно эти силы в рамках полуклассической теории.

Выберем неинерциальную систему отсчета, связанную с электроном. В системе координат электрон неподвижен и его момент равен нулю:

Однако электрон обладает спиновым магнитным моментом пропорциональный . В этой системе координат ядро движется и по закону Био-Савара-Лапласа создает магнитное поле:.

где определяет орбиту.

Каждый уровень, у которого , тогда каждый уровень должен расщепляться на два подуровня.

Если то- уровень одиночный.

В третьем опыте: - магнитный момент для любой системы.

gl=1.

gs=2.

Кварцевая нить помещена в катушку с проволкой.

H-кварцевая нить с известным коэффициентом упругости;

C-ферромагнитный стержень;

К-катушка с проволкой;

З-зеркало;

S-источник света;

Ш-шкала для измерения углового положения светового зайчика.

В начальный момент стержень был не намагничен, так как все атомные магнитные моменты были ориентированы хаотически. После включения тока в катушке возникло продольное магнитное поле и стержень намагничевался, приобретая магнитный момент единицы объема Кроме того стержень приобрел и механический момент. Однако для замкнутых систем выполняется закон сохранения вращательного момента и, следовательно, стержень должен повернуться. Зная коэффициент упругости нити и угол поворота можно определить вращательный момент. Для известной конструкции катушки можно также измерить и величину, следовательно, можно измерить отношениеMкG, значит явление ферромагнетизма носит число квантовых спиновых происхождений.

Замечание: наличие спина является атрибутам не только электронов.

Есть частицы с нулевым спином s=0, п, к-мезоны.

Покажем, что наглядно спин нельзя представить вращение шарика вокруг своей оси:

Предположим, что вся масса электрона сосредоточена по экватору.

, .

Возьмем эксперимент с ипосмотрим с какой скоростью будет двигаться электрон: