Глава 4. Движение микрочастиц в центрально симметричных полях.

Поле U=U(r) называется центрально симметричным, если потенциальная энергия частицы зависит от расстояния до некоторого силового центра и не зависит от углов.

§ 1. Разделение переменных в уравнении Шредингера для центрально симметричного поля.

В центральных полях весь анализ удобно проводить в сферических координатах r, ,:

,

,

.

Элемент объема: .

Оператор Лапласа:

.

Введем следующие обозначения:

,

,

,

,

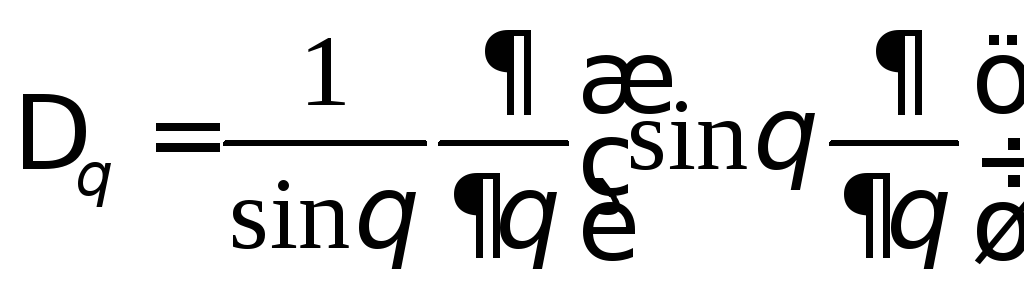. (1)

Пусть частиц массой m₀ движется в некотором произвольном центральном поле U(r). Движение микрочастицы описывается трехмерным стационарным уравнением Шредингера:

,

-дифференциальное уравнение второго порядка в частных производных.

Будем искать решение этого уравнения методом разделения переменных: подставим вида (1) в уравнение Шредингера, имеем:

,

,

.

Умножим все члены последнего уравнения на :

.

В последнем уравнении левая часть зависит только от r, а правая лишь от угловых переменных . И это равенство должно выполняться при всех значениях (r,,), но это возможно лишь в том случае, если правая и левая части. Тогда переходим к двум независимым уравнениям:

Отсюда видно, что силовое поле U(r) определяет поведение радиальной части волновой функции R(r), поэтому это уравнение называется радиальным уравнением Шредингера. При этом угловая часть является универсальной для всех центрально симметричных полей.

Рассмотрим уравнение для функции Y (угловой части):

.

Разделим переменные и в этом уравнении, для этого запишем угловую часть в виде произведения двух функций: .

.

Умножим все члены на :

.

Получаем два независимых уравнения:

Найдем решение последних двух уравнений:

, .

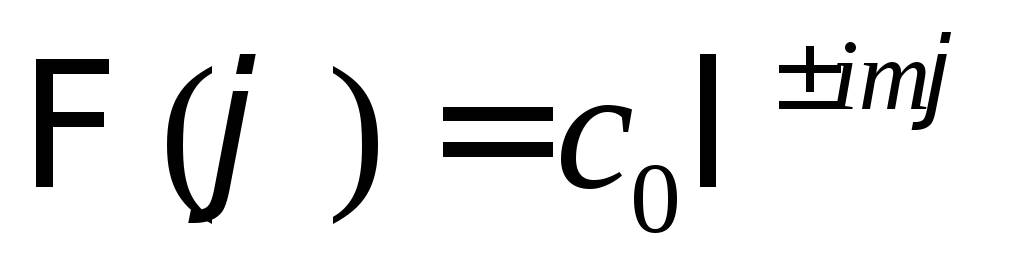Если число m можем принимать как положительные, так и отрицательные значения, то общее решение можно записать в виде одной экспоненты:

.

Надо потребовать для условия однозначности:

,

.

, -магнитное квантовое число.

Рассмотрим уравнение: .

Имеет решение удовлетворяющее стандартным условиям, если выполнены два требования или два условия:

1. ,l=0,1,2,...

2. ,, (2l+1-дискретных значения).

При этом решение имеют вид:.

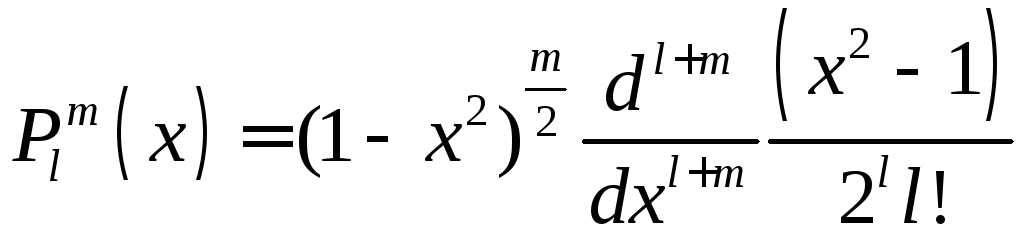- присоединенные полиномы Лежандра.

Коэффициенты c и c₀ находят из условия нормировки:

,

,

.

Приведем некоторые частные производные функции :

1. l=0, m=0, .

2. l=1, , , , .

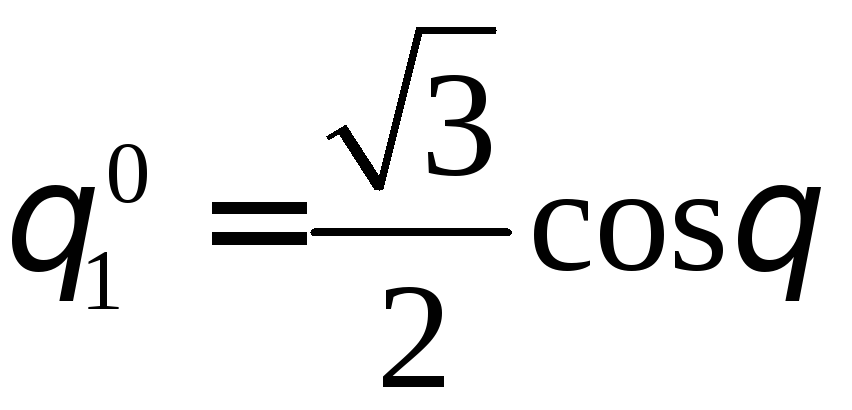В любых центральных полях угловая часть волновой функции зависит от двух дискретных индексов l и m:

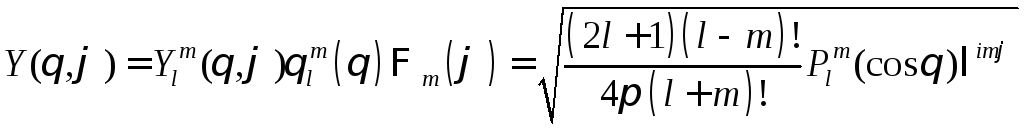-шаровая функция.

l=0,1,2,... (орбитальное квантовое число), (магнитное квантовое число).

§ 2. Операторы момента импульса, их собственные функции и их собственные значения.

Операторы момента импульса имеют вид:

,

,

,

.

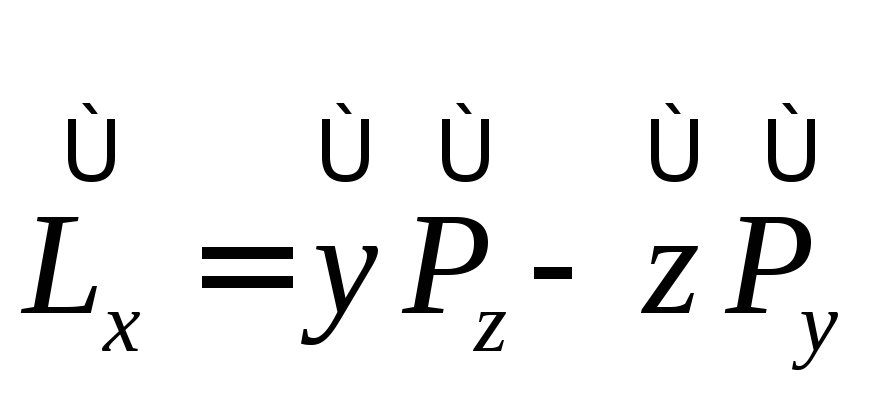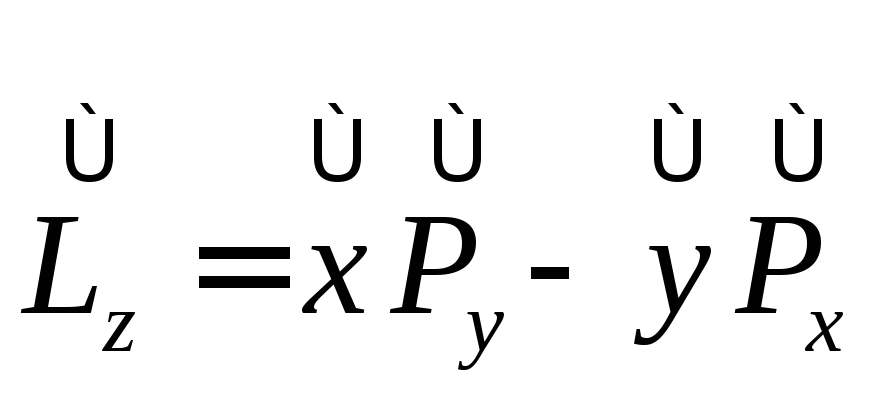Учитывая коммутированные свойства операторов координаты и импульса:

, ,.

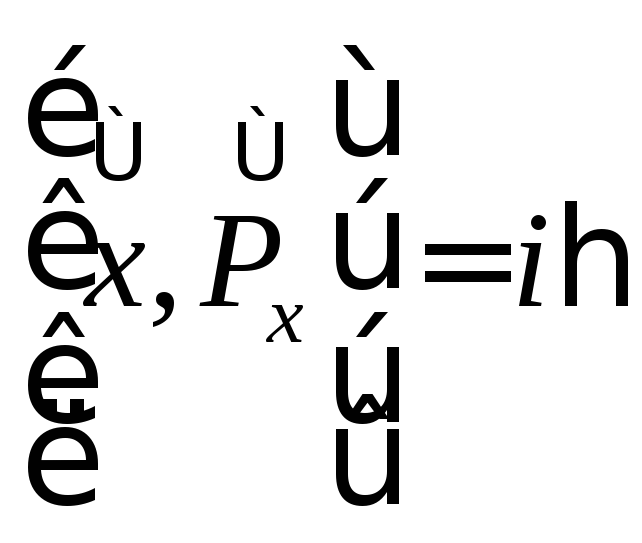Опираясь на эти коммутационные соотношения:

, можно воспользоваться правилом циклической подстановки.

,

,

.

Из приведенных коммутационных условий следуют два условия:

1. Невозможность одновременного измерения двух любых проекций момента импульса.

2. Возможно измерить квадрат момента импульса вместе с любой своей проекцией.

В дальнейшем будем считать ,. Покажем, что шаровая функция:

является собственной функцией операторов ,. Запишем операторы,в сферических координатах:

, .

Покажем теперь, что шаровая функция является собственной функцией:

, следовательно, - в этом состоит физический смысл магнитного квантового числа.

,

.

-формула квантования для длины волны.

В спектроскопии атома орбитальное квантовое число l принято записывать в виде маленькой латинской буквы: l=0,1,2,3,4,5,6,7,8

s,p,d,f,g,h,i,j,k

Если электрон находится в d-состоянии, это означает, что l=2, и имеет пять проекций.