III. Уравнение Шредингера и его следствия
Уравнение непрерывности в квантовой механике имеет вид:
а)
,
б)
,
с)
,
д)
.
Волновая функция частицы равна ψ(х) = Аsinх. Вероятность обнаружения частицы в пространстве равна:
а) Аsinх,
б) Асоsх,
с) А²sin²х,
д) А².
Волновая функция частицы равна ψ(х) = А sinх. Плотность тока вероятности равна:
а) А²sin²х,
б) Асоs²х,
с) 0,
д) Аsin2х.
Волновая функция частицы равна ψ(х) = Аеiрх/ћ. Вероятность обнаружения частицы в пространстве равна:
а)
,
б) А² х² ,
с) А² р²,
д) |А|².
Волновая функция частицы равна ψ(х) = Аеiрх/ћ. Плотность тока вероятности равна:
а)
|А|²
,
б) А² р²,
с) А² х²,
д) |А|²
.
Оператор Â явно от времени не зависит. Найти производную
.
а) 0,
б)
,
с)
,
д) 
.
Свободно движущаяся частица имеет энергетический спектр, который является:
а) непрерывным,
б) дискретным и действительным,
с) зависящим от массы частицы,
д) дискретным и комплексным.
Вычислить производную по времени
.
а) 2
,
б)
,
с)
,
д)
.
Вычислить производную по времени
.
а) 
,
б)
,
с)
,
д)
.
Вычислить производную по времени
для частицы, движущейся в потенциальном
полеU(x).
а) 
,
б) 
,
с) 
+
,
д)
– (
+
).
Какие физические величины (Е, рх, Lх, L²) являются интегралами движения при свободном движении микрочастицы?
а) Е,
б) Е, рх,
с) Е, рх, Lх, L²,
д) указанные величины не сохраняются.
Среднее значение х-координаты частицы, состояние которой определяется волновой функцией ψ(х), равно:
а)
,
б) 
,
с)
,
д) 
.
Среднее значение проекции импульса частицы рх, состояние которой определяется волновой функцией ψ(х), равно:
а) 
,
б) 
,
с)
,
д)
–
.
Частица движется в потенциальном поле U(z) = аz, где а = const. Какие проекции импульса (рх, ру, рz) сохраняются в этом поле?
а) рх, ру,
б) рz,
с) рх, ру, рz,
д) рх, рz.
Частица движется в потенциальном поле U(z) = аz, где а = const. Какие проекции момента импульса (Lх, Lу, Lz) сохраняются в этом поле?
а) Lх,
б) Lу,
с) Lz,
д) Lх, Lу, Lz.
Частица движется в стационарном поле
.
Производная по времени
равна:
а) z
,
б) y
,
с) y
– z
,
д)
z
– y
.
Частица движется в стационарном поле
.
Производная по времени
равна:
а)
x
–
z
,
б) z
– x
,
с) x
,
д) y
.
Частица движется в стационарном поле
.
Производная по времени
равна:
а) x
+ y
,
б)
y
– x
,
с) x
,
д) y
.
Имеются два произвольных оператора Â и Ĉ. Какое из равенств является верным?
а)
(ÂĈ)
=
Ĉ,
б)
(ÂĈ)
= Â
,
с)
(ÂĈ)
= [Â,Ĉ],
д)
(ÂĈ)
=
Ĉ
+ Â
.
Среднее значение квадрата величины А вычисляется по формуле
.
Каким свойством должен обладать операторÂ?
а) Â – линейный,
б) Â – не эрмитовый,
с) Â – эрмитовый,
д) Â – любой.
Две волновые функции частицы ψ1 и ψ2 связаны условием ψ2 = = 2ψ1. Как связаны вероятности нахождения частицы в точке х(W1, W2)?
а) W1 = W2,
б) W1 = 2W2,
с) W2 = 2W1,
д) W2 = 4W1.
Волновая функция ψ (х) называется нормированной, если выполняется условие:
а)
= 1,
б)
= 1,
с)
= 1,
д) ψ* = ψ.
Стационарное одномерное уравнение Шредингера в поле U(х) имеет вид:
а) ψ´´
+
ψ
= 0,
б) ψ´
+
ψ
= 0,
с)
ψ´´
+
ψ
= 0,
д) ψ´´
+
ψ
= 0.
(символ штрих означает производную по координате)
Принцип причинности в квантовой механике позволяет:
а) обосновать принцип запрета Паули,
б) построить волновую функцию ψ(х,t) при t > 0 для заданной ψ(х,0),
с) построить волновую функцию ψ(х,t) при t > 0 для заданных ψ(х,0) и ψ´(х,0),
д) рассчитать траекторию движения микрочастицы.
(символ штрих означает производную по координате).
Равенство
=
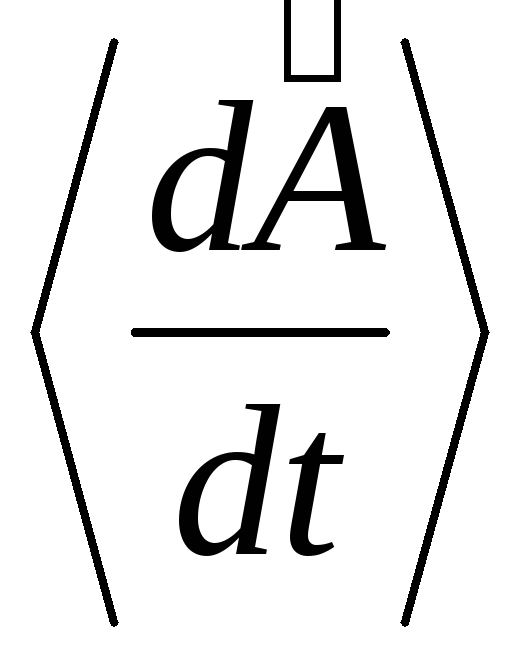выполняется:
а) всегда,
б) только для линейных операторов,
с) только для эрмитовых операторов,
д) только для стационарных силовых полей.
В каком случае собственное значение λ оператора Â будет сохраняться о времени?
а) Â – эрмитовый оператор,
б)
= 0,
с)
= 0 и
=
0,
д)
=
0.
В каких силовых полях
проекция момента импульсаLz
будет интегралом движения?
а)
,
б)
,
с)
,
д)
.
В каких силовых полях
проекция момента импульсаLz
сохраняется?
а)
,
б)
,
с)
,
д)
.
Частица движется в потенциальном поле U(х) = ах, где а = const. Вычислить коммутатор
.
а) 0,
б) а,
с)
–
а,
д) 
а.
Частица движется в потенциальном поле U(х) = ах, где а = const. Вычислить коммутатор
.
а) а, б)
–
а, с)
а, д)
0.