Лекции / №9

9.Формула полного математического ожидания. Улутшение несмещенной оценки посредством усреднения по достаточной ст-ке.

Пусть - это некоторая функция случайной величины . Тогда по определению математического ожидания можно записать , где - это плотность распределения вероятностей случайной величины . Воспользуемся выражением условной вероятности через безусловную . Из (1) получим: . . Формула (2) называется формулой полного математического ожидания. Полагая в формуле (2) , получим . Аналогичным образом можно доказать, что дисперсия . , зн.

Сущ-ие минимальных оценок с мин-ыми оценками.

Пусть V-это несмещенная оценка для параметра , т. е. . И пусть S это достаточная статистика для .

Введем ф.-ю и будем считать, что эта ф.-я зависит только от S.

Покажем теперь, что Т является несмещенной оценкой для .

Действ., .

Покажем, что дисперсия оценки Т меньше, чем V.

Найдем дисперсию

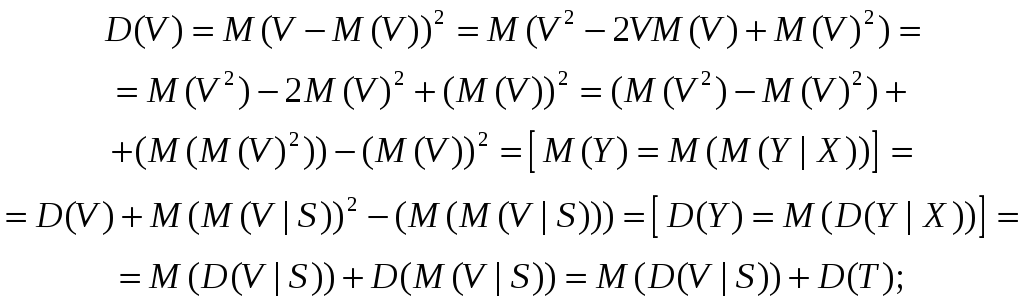
т. е. дисперсия действ. стала меньше.

Равенство достигается в том и только том случае, когда , т. е. когда V явл. ф.-ей от S с вероятностью 1. Пусть теперь имеется две различные несмещенные оценки и и для них и . Эти оценки и явл.-ся такими ф.-ми от S, что для всех вып-ся рав-во . Действ., .

Если S- полная достаточная статистика (полнота означает, что , если ), то рав-во выполняется только том случае, когда . Т. о. любая ф.-я полной достаточной статистики явл.-ся един.-й несмещенной оценкой ми-ной дисперсией для своего математического ожидания.

Описанный метод ценен в основном в теоретическом плане. Иногда он полезен для построения несмещенных оценок, но его можно использовать только для относительно простых задач.