
Авиационная электросвязь / 12.Частотная модуляция
.docxЛекция 12
Частотная модуляция
Частотная модуляция (ЧМ) — вид аналоговой модуляции, при котором информационный сигнал управляет частотой несущего колебания. По сравнению с амплитудной модуляцией здесь амплитуда остаётся постоянной.
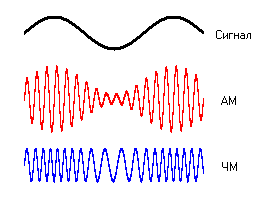
Пример частотной модуляции. Вверху — информационный сигнал на фоне несущего колебания. Внизу — результирующий сигнал
Применение:
Частотная модуляция применяется для высококачественной передачи звукового (низкочастотного) сигнала в радиовещании (в диапазоне УКВ), для звукового сопровождения телевизионных программ, видеозаписи на магнитную ленту, музыкальных синтезаторах.
Высокое качество кодирования аудиосигнала обусловлено тем, что при ЧМ применяется большая (по сравнению с шириной спектра сигнала АМ) девиация несущего сигнала, а в приёмной аппаратуре используют ограничитель амплитуды радиосигнала для ликвидации импульсных помех.
Частотная
модуляция (ЧМ)
заключается в изменении частоты
генерируемых колебаний на величину
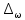 ,
пропорциональную изменению уровня
модулирующего сигнала, представленного
формулой (1.26)
,
пропорциональную изменению уровня
модулирующего сигнала, представленного
формулой (1.26)
Постоянный
уровень
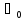 этого сигнала соответствует
немодулированному колебанию несущей
частоты
этого сигнала соответствует
немодулированному колебанию несущей
частоты
 (t)=
(t)= +
+ cos
cos t
(1.26)
t
(1.26)
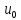 (t)=
(t)=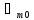 cos
cos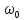 t
(1.27)
t
(1.27)


а фаза
 (1.31)
(1.31)
то
для неизменной частоты
 ;
;
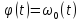 ,
а выражение (1.27) записываетсяс в виде:
,
а выражение (1.27) записываетсяс в виде:
 (t)=
(t)=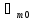 cos
cos t)
(1.32)
t)
(1.32)
Исходя из сущности частотной модуляции, можно записать мгновенное значение частоты, полагая, что модулирующий сигнал изменяется по гармоническому закону в соответствии с выражением (1.26):
 +∆
+∆ cos
cos t
(1.33)
t
(1.33)
Интегрирование выражения (1.32) согласно формуле (1.31) дает следующий результат:
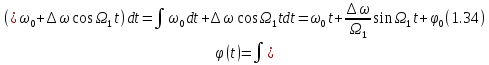
Заменяя
 в формуле (1.32) выражением (1.34) и положив
что удобства последующих преобразований
в формуле (1.32) выражением (1.34) и положив
что удобства последующих преобразований
 получаем ЧМ сигнал:
получаем ЧМ сигнал:

Отношение
 называется индексом модуляции и
обозначается символом
называется индексом модуляции и
обозначается символом
 .
Разделив
числитель и знаменатель этого отношения
на 2π, получим
.
Разделив
числитель и знаменатель этого отношения
на 2π, получим
 =
=
где

Для рассмотрения спектра ЧМ сигнала (рис. 1.18) следует прибегнуть к известному расположение выражения (1.35) в ряд [5]:
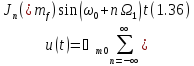
где
 (
( -
функция
Бесселя n-го
порядка 1-го рода.
-
функция
Бесселя n-го
порядка 1-го рода.
При
n
целом
 поэтому ряд (1.36) можно представить в
виде:
поэтому ряд (1.36) можно представить в
виде:
 (
( )
) (
( )
[
)
[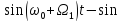 (
(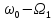 )
t ] +
)
t ] +
 (
(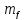 )
[
)
[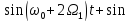 (
( )
t ] +
)
t ] + (
( )
[
)
[ (
( )
t ]+….} (1.37)
)
t ]+….} (1.37)
Выражение (1.37) показывает, что спектр амплитуд ЧМ сигнала содержит колебания несущей частоты и боковых составляющих первой и высших гармоник модулирующего сигнала, число которых бесконечно велико. Амплитуды боковых составляющих спектра пропорциональны бесселевым функциям, зависимость которых от индекса модуляции представлена на рисунках.

Рис.1. Временные диаграммы а – модулирующий сигнал; б – колебания с ЧМ.

Рис. 2. Функции Бесселя.
Графики
беселевых функций показывают, что при
малых индексах модуляции ( амплитуды высших гармонических
составляющих спектра сигнала близки к
нулю. В этом случае он по ширине и составу
не отличается от спектра АМ.
амплитуды высших гармонических
составляющих спектра сигнала близки к
нулю. В этом случае он по ширине и составу
не отличается от спектра АМ.
С
ростом
 убывает
до нуля, а боковые составляющие
увеличиваются, и возрастает значимость
высших гармоник. Происходит расширение
полосы частот спектра. Дальнейшее
увеличение
убывает
до нуля, а боковые составляющие
увеличиваются, и возрастает значимость
высших гармоник. Происходит расширение
полосы частот спектра. Дальнейшее
увеличение
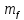 ведет к волнообразному изменению
амплитуды несущей частоты и еще большему
расширению спектра. На рис. 3 показаны
спектры сигналов с ЧМ для трех значений
индекса модуляции 1, 2, 4. Из приведенных
примеров следует, что ширина спектра
практически может быть ограничена
боковыми частотами, которые образуются
гармониками сигнала с номером, равным
индексу модуляции. Таким образом, при
m
≥ 1 ширина спектра примерно равна
удвоенному значению девиации частоты.
2
ведет к волнообразному изменению
амплитуды несущей частоты и еще большему
расширению спектра. На рис. 3 показаны
спектры сигналов с ЧМ для трех значений
индекса модуляции 1, 2, 4. Из приведенных
примеров следует, что ширина спектра
практически может быть ограничена
боковыми частотами, которые образуются
гармониками сигнала с номером, равным
индексу модуляции. Таким образом, при
m
≥ 1 ширина спектра примерно равна
удвоенному значению девиации частоты.
2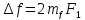 ,
что согласуется с физическим смыслом
частотной модуляции.
,
что согласуется с физическим смыслом
частотной модуляции.
Рис.3. Спектры ЧМ колебаний. Зависимость спектров от коэффициента модуляции.
При
увеличении индекса модуляции
 возникают ряды
возникают ряды


в
спектре ЧМ появляются частоты
 .
При больших
.
При больших
 ширина спектра
ширина спектра
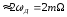 ,
причем несущая подавлена до уровня
остальных составляющих :
,
причем несущая подавлена до уровня
остальных составляющих :

Основное
применение ЧМ - высококачественное
радиовещание (при девиации частоты
~100KHz - т.е. с
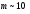 )
в диапазоне УКВ (60-100MHz) и в каналах
передачи звука в телевещании. Причина
- низкая чувствительность к паразитной
амплитудной модуляции и к помехам.
)
в диапазоне УКВ (60-100MHz) и в каналах
передачи звука в телевещании. Причина
- низкая чувствительность к паразитной
амплитудной модуляции и к помехам.
