
РГР 2
.docxВопросы к защите РГР №2 по математике за 1 семестр.
-
Определение вектора, длины вектора.
Вектор - это направленный отрезок, который имеет начало и конец.
Длиной
ненулевого вектора
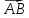 называется
длина отрезка AB.
называется
длина отрезка AB.
-
Определение нулевого вектора.
Нулевой вектор — вектор, начало которого совпадает с его концом.
-
Определение ортов.
Орты – единичный вектор.
-
Определение коллинеарных и компланарных векторов.
Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.
Векторы называются компланарными, если существует плоскость, которой они параллельны.
-
Определение суммы векторов.
Чтобы
сложить два вектора, нужно от конца
одного из них отложить второй вектор;
тогда сумма – это вектор с началом в
начале первого вектора и концом в конце
второго вектора: 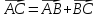 .
.
-
Определение разности векторов.
Разностью
двух векторов
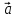 и
и 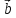 называется
такой третий вектор
называется
такой третий вектор  ,
который равен сумме векторов
,
который равен сумме векторов 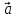 и
и 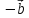 .
.
-
Определение проекции вектора на ось.
Проекцией вектора 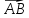 на
ось
l называется
длина его составляющей
на
ось
l называется
длина его составляющей 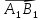 по
этой оси, взятая со знаком «+», если
по
этой оси, взятая со знаком «+», если 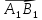 сонаправлен с l,
и со знаком «-»,если
сонаправлен с l,
и со знаком «-»,если 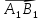 не
сонаправлен с l.
не
сонаправлен с l.
-
Определение разложения вектора по ортам.
Разложение вектора по ортам имеет вид:

-
Длина вектора в координатной форме.
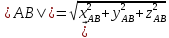
![]()
-
Сумма и разность векторов в координатной форме.
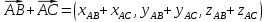
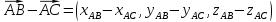
-
Равенство векторов в координатной форме.
Два вектора называются равными, если они сонаправленные и имеют равные модули.

-
Коллинеарность векторов в координатной форме.
a={ax; ay; az} и b={bx; by; bz} коллинеарны если
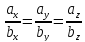
-
Определение радиус-вектора точки.
Радиус-вектор точки - называется вектор, начало которого совпадает с началом системы координат, а конец - с данной точкой.
-
Определение скалярного произведения векторов.
Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.
-
Вычисление скалярного произведения в координатной форме.
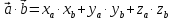
-
Условие перпендикулярности двух векторов в векторной и координатной форме.
Для
перпендикулярности двух ненулевых
векторов
 и
и
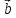 необходимо и достаточно, чтобы их
скалярное произведение равнялось нулю,
то есть, чтобы выполнялось равенство
необходимо и достаточно, чтобы их
скалярное произведение равнялось нулю,
то есть, чтобы выполнялось равенство
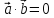 .
.
Необходимое
и достаточное условие перпендикулярности
двух векторов в координатах имеет вид
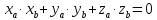 .
.
-
Формула вычисления угла между двумя векторами.
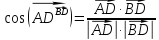
-
Определение векторного произведения векторов.
Векторным
произведением вектора 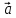 на
вектор
на
вектор 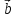 называется
третий вектор
называется
третий вектор 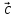 который
обладает следующими свойствами:
который
обладает следующими свойствами:
-
Его длина равна
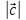 =
=
-
Вектор
 перпендикулярен
к плоскости, в которой лежат вектора
перпендикулярен
к плоскости, в которой лежат вектора 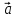 и
и 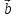
-
Вектор
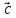 направлен
так, что поворот от вектора
направлен
так, что поворот от вектора 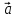 к
вектору
к
вектору 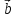 осуществляется
против часовой стрелки, если смотреть
из конца вектора
осуществляется
против часовой стрелки, если смотреть
из конца вектора 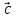 (в
этом случае, говорят, что тройка
векторов
(в
этом случае, говорят, что тройка
векторов 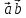 и
и 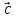 –
правая).
–
правая).
-
Вычисление векторного произведения в координатной форме.
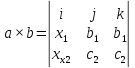
-
Геометрический смысл векторного произведения.
Геометрический смысл векторного произведения: модуль векторного произведения векторов численно равен площади параллелограмма, построенного на этих векторах как на сторонах.
-
Определение смешанного произведения векторов.
Смешанное произведение векторов a, b, c — скалярное произведение вектора a на векторное произведение векторов b и c.
-
Вычисление смешанного произведения в координатной форме.
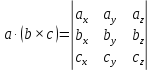
-
Геометрический смысл смешанного произведения.
Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами a, b, c.
-
Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.
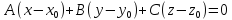
-
Общее уравнение плоскости.
Ax + By + Cz + D = 0
-
Какой геометрический смысл имеют коэффициенты в общем уравнении плоскости?
Геометрическое значение коэффициентов A, B и C в общем уравнении плоскости Ax + By + Cz + D = 0 состоит в том, что они являются проекциями на координатные оси Ox, Oy, Oz вектора, перпендикулярного этой плоскости.
-
Частные случаи общего уравнения плоскости.
1) By + Cz + D = 0 - параллельна оси Ox;
2) Ax + Cz + D = 0 - параллельна оси Oy;
3) Ax + By + D = 0 - параллельна оси Oz;
4) Cz + D = 0 - параллельна оси Oxy;
5) By + D = 0 - параллельна оси Oxz;
6) Ax + D = 0 - параллельна оси Oyz;
7) Ax + By + Cz = 0 - проходит через начало координат;
8) By + Cz = 0 - проходит через ось Ox;
9) Ax + Cz = 0 - проходит через ось Oy;
10) Ax + By = 0 - проходит через ось Oz;
11) z = 0 - плоскость Oxy;
12) y = 0 - плоскость Oxz;
13) x = 0 - плоскость Oyz.
-
Уравнение плоскости, проходящей через три данные точки.
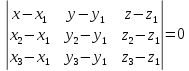
-
Угол между двумя плоскостями.
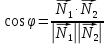
-
Условия параллельности и перпендикулярности двух плоскостей.
Две
плоскости параллельны тогда и только
тогда, когда их нормальные векторы
параллельны, а значит
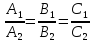 .
.
Две
плоскости перпендикулярны тогда и
только тогда, когда их нормальные векторы
перпендикулярны, а значит
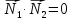 .
.
-
Расстояние от точки до плоскости.
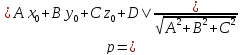
-
Канонические уравнения прямой.
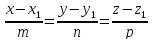
-
Какой геометрический смысл имеют коэффициенты, входящие в канонические уравнения прямой?
m, n, p – направляющий вектор прямой
-
Уравнение прямой в пространстве, проходящей через две заданные точки.
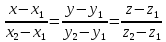
-
Параметрические уравнения прямой в пространстве.
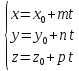
-
Угол между прямыми в пространстве.

-
Условия параллельности и перпендикулярности двух прямых в пространстве.
Чтобы две прямые были параллельны необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, т.е. их соответствующие координаты были пропорциональны.
Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю (скалярное произведение).
-
Угол между прямой и плоскостью.
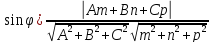
-
Условия параллельности и перпендикулярности прямой и плоскости.
Для того, чтобы прямая и плоскость были параллельны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были перпендикулярны. Для этого необходимо, чтобы их скалярное произведение было равно нулю.
Для того, чтобы прямая и плоскость были перпендикулярны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были коллинеарные. Это условие выполняется, если векторное произведение этих векторов было равно нулю.
-
Как найти координаты точки пересечения прямой и плоскости.
-
Привести уравнение прямой к параметрическому виду:
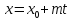 ;
;
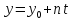 ;
;
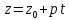
-
Подставить эти выражения в уравнение плоскости.
-
Из полученного найти t, а потом x,y и z.
