§3.1. Механические затухающие колебания.

Механическая система: пружинный маятник с учетом сил трения. Силы, действующие на маятник:

1.       Упругая сила. , где  k – коэффициент жесткости пружины, х – смещение маятника от положения равновесия.

2.       Сила сопротивления. Рассмотрим силу сопротивления, пропорциональную скорости v движения (такая зависимость характерна для большого класса сил сопротивления): . Знак «минус» показывает, что направление силы сопротивления противоположно  направлению скорости движения тела. Коэффициент сопротивления r численно равен силе сопротивления, возникающей при единичной скорости движения тела:

 

.

 

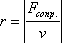Закон движения пружинного маятника – это второй закон Ньютона: ma = F_упр. + F_сопр. Учитывая, что

 

 и , запишем второй закон Ньютона в виде: .

 

 

Разделив все члены уравнения на m, перенеся их все  в правую часть, получим дифференциальное уравнение затухающих колебаний:

 

.

 

Обозначим ,  где β – коэффициент затухания,  , где  ω₀ – частота незатухающих свободных колебаний в отсутствии потерь энергии в колебательной системе. В новых обозначениях дифференциальное уравнение затухающих колебаний имеет вид:

 

.

 

Это линейное дифференциальное уравнение второго порядка. Уравнение затухающих колебаний  есть решение такого дифференциального уравнения:

 

, .

 

В приложении 1 показано получение решения дифференциального уравнения затухающих колебаний методом замены переменных. Частота затухающих колебаний:

(физический смысл имеет только вещественный корень, поэтому ).