§1.2. Зависимость амплитуды и начальной фазы колебаний от начальных условий.

Решения дифференциального уравнения колебаний определены с точностью до постоянной величины, поэтому таких решений бесчисленное множество. Выбор решения для данной конкретной колебательной системы можно сделать, если задать ее поведение в начальный момент времени, то есть начальные условия. Например, если просто отклонить маятник, растянув пружину, а затем спокойно отпустить его, или отклонить, а затем подтолкнуть маятник, то движения маятника будут различными. Рассмотрим зависимость параметров колебательной системы от  начальных условий.

Пусть при t = 0 смещение системы от положения равновесия равно х₀, а начальная скорость v₀. Гармоническое колебание описывается уравнением . При t = 0 имеем два уравнения: ,  . Возведя в квадрат оба уравнения и сложив их, получим уравнение для амплитуды:

.

 

Поделив одно уравнение на другое, получим соотношение для начальной фазы:

.

 

Таким образом, и амплитуда, и начальная фаза колебаний зависят от начальных условий колебательной системы.

 

§1.3. Свободные гармонические колебания в lc-контуре.

1.                      Электромагнитный контур состоит из плоского конденсатора емкостью С и катушки индуктивности (соленоида) с индуктивностью L. Такой контур называется идеальным контуром с сосредоточенными параметрами. Конденсатор зарядили, на одной пластине заряд +q, на другой  (–q).

Рассмотрим процессы в LC – контуре за время T, называемое периодом колебаний. Момент времени t = 0. Конденсатор заряжен, ключ «К» разомкнут, ток в контуре не идет: I = 0,

 

,   

 

Ключ замкнут, по цепи идет ток разрядки до тех пор, пока не выровняются потенциалы обкладок конденсатора. При  

 

 Когда конденсатор разрядится, ток разрядки прекратится. Магнитное поле в катушке индуктивности, не поддерживаемое током, начнет уменьшаться. Уменьшение магнитного поля вызовет уменьшение магнитного потока сквозь площадь катушки, возникнет ЭДС индукции. По цепи контура пойдет индукционный ток того же направления, что и ток разрядки (правило Ленца). Это приведет к перезарядке конденсатора. При    

  Направление тока разрядки в контуре изменится. Ток разрядки будет идти по цепи до выравнивания потенциалов на обкладках конденсатора.

 

При При t = T система вернется в исходное положение.

В рассмотренном LC – контуре происходит превращение энергии из одного вида в другой и обратно, полная энергия контура - величина постоянная    . Периодические изменения вектора напряженности Е электрического поля и вектора магнитной индукции В магнитного поля в закрытом колебательном  LC – контуре называется электромагнитными колебаниями.

2. Используем 2-й закон Кирхгофа для получения дифференциального уравнения электромагнитных колебаний. Для любого замкнутого контура алгебраическая сумма падений напряжений на всех его участках равна алгебраической сумме ЭДС, действующих в этом контуре (2-е правило Кирхгофа). Падение напряжения на обкладках конденсатора в LC – контуре равно

 

 

где q – величина заряда на обкладках, С – емкость конденсатора. ЭДС индукции, возникающая в катушке индуктивности при изменении тока в ней, определяется формулой:

 

 

 (закон электромагнитной индукции Фарадея). Второе правило Кирхгофа для LC – контура имеет вид:

 

 или  .

 

По определению сила тока равна первой производной по времени от заряда ,  тогда  . Преобразуем уравнение 2-ого закона Кирхгофа, получим

 

Обозначим   , получим окончательно уравнение вида:

 

Это линейное дифференциальное уравнение второго порядка, решениями которого являются функции   или . И дифференциальное уравнение для электромагнитных колебаний, и его решения подобны тем, которые получены для механической системы (пружинного маятника). Величины, входящие в уравнения электромагнитных колебаний, имеют следующий смысл: q0 – амплитуда заряда – максимальный заряд конденсатора; q –  величина заряда на обкладках конденсатора в момент времени t;  – фаза колебаний – величина, определяющая заряд конденсатора в любой момент времени t; α – начальная фаза определяет заряд конденсатора в начальный момент времени (t = 0).

Циклической  частотой  периодических колебаний в LC – контуре является величина  .

 

Период колебаний равен  (формула Томсона).

Определим зависимость силы тока, ЭДС и энергии  колебаний от времени в LC – контуре. Уравнение изменения заряда на обкладках конденсатора возьмем в  виде:  . Сила тока  в контуре определяется соотношением:

 

.

 

Величину  называют амплитудой  силы тока. Уравнение для ЭДС имеет вид:

 

.

 

Величина  – амплитуда  ЭДС. Электрическая и магнитная энергия изменяется согласно уравнениям:

 

 

 

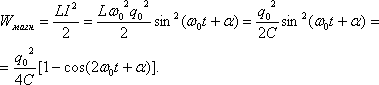
Полная энергия колебаний в LC - контуре   не зависит от времени (закон сохранения энергии). Графики зависимостей от времени t физических величин, характеризующих электромагнитных колебаний в LC – контуре, аналогичны графикам для механических колебаний (см. Рисунок 1.2). Если заряд на обкладках изменяется по закону , т.е. начальная фаза α = 0, то его график  такой же как график смещения.

Напряжение между обкладками конденсатораизменяется по тому же закону, что и заряд конденсатора, только амплитуда напряжения будет другой . Изменение силы тока аналогично изменению скорости тела при механических незатухающих колебаниях. W_эл. изменяется  как  W_пот.,  а  W_магн.  - как  W_кин..