29. Преобразование Лапласа. Свойство подобия.
Преобразова́ние
Лапла́са —
интегральное преобразование, связывающее
функцию 
комплексного
переменного (изображение)
с функцией 
вещественного
переменного (оригинал).
С его помощью исследуются свойства динамических
систем и
решаются дифференциальные и интегральные
уравнения.
Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так, свёртка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими.
Прямое преобразование Лапласа[править | править исходный текст]
Преобразованием
Лапласа функции вещественной
переменной 
,
называется функция 
комплексной
переменной 
[1],
такая что:
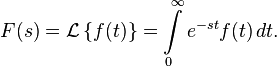
Правая часть этого выражения называется интегралом Лапласа.
Обратное преобразование Лапласа[править | править исходный текст]
Обратным
преобразованием Лапласа функции комплексного
переменного 
,
называется функция 
вещественной
переменной, такая что:
где 
—
некоторое вещественное число (см. условия
существования).
Правая часть этого выражения
называется интегралом
Бромвича.
Двустороннее преобразование Лапласа[править | править исходный текст]
Основная статья: Двустороннее преобразование Лапласа
Двустороннее
преобразование Лапласа — обобщение
на случай задач, в которых для
функции 
участвуют
значения 
.
Двустороннее преобразование Лапласа определяется следующим образом:
Дискретное преобразование Лапласа[править | править исходный текст]
Применяется в сфере систем компьютерного управления. Дискретное преобразование Лапласа может быть применено для решётчатых функций.
Различают 
-преобразование
и 
-преобразование.
-преобразование
Пусть 
—
решётчатая функция, то есть значения
этой функции определены только в
дискретные моменты времени 
,
где 
—
целое число, а 
—
период дискретизации.
Тогда, применяя преобразование Лапласа, получим:
-преобразование
Основная статья: Z-преобразование
Если применить следующую замену переменных:
получим 
-преобразование:
2.Теорема подобия. Для любого постоянного a >0
.
61. Разложение в ряд Фурье четных и нечетных функций
Пусть f(x) - четная функция с периодом 2L, удовлетворяющая условию f(-x) = f(x) .
Тогда для коэффициентов ее ряда Фурье находим формулы:
=
=
=
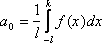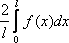
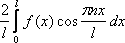
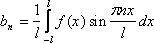0
,
где n=1,2,
...
Таким образом, в ряде Фурье для четной функции отсутствуют члены с синусами, и ряд Фурье для четной функции с периодом 2L выглядит так:
Пусть теперь f(x) - нечетная функция с периодом 2L, удовлетворяющая условию f(-x) = - f(x).
Тогда для коэффициентов ее ряда Фурье находим формулы:
,
где n=1,2,
...
Таким образом, в ряде Фурье для нечетной функции отсутствует свободный член и члены с косинусами, и ряд Фурье для нечетной функции с периодом 2L выглядит так:
Если
функция f(x)
разлагается в тригонометрический ряд
Фурье на промежутке
то 
,
где 
,
,
,
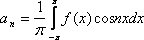Если f(x) разлагается в тригонометрический ряд Фурье на [0,L], то доопределив заданную функцию f(x) соответствующим образом на [-L,0]; далее периодически продолжив на (T=2L), получим новую функцию, которую разлагаем в тригонометрический ряд Фурье.
Для разложения в ряд Фурье непериодической функции, заданной на конечном произвольном промежутке [a,b], надо : доопределить на [b,a+2L] и периодически продолжить, либо доопределить на [b-2L,a] и периодически продолжить.
Билет.30