55.Биноминальный ряд
БИНОМИАЛЬНЫЙ РЯД - степенной ряд вида
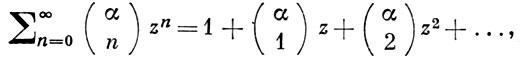
где n - целое, а α - произвольное фиксированное число (вообще говоря, комплексное), z = x + iy - комплексное переменное, (αn) - биномиальные коэффициенты. Для целых α = m ≥ 0 Б. р. сводится к конечной сумме m + 1 слагаемых
называемой Ньютона биномом. Для остальных значений α Б. р. абсолютно сходится при |z| < 1 и расходится при |z| > 1. В граничных точках единичной окружности |z| = 1 Б. р. ведет себя следующим образом: 1) если Re α > 0, то он абсолютно сходится во всех точках окружности |z| = 1; 2) если Re α ≤ - 1, то он расходится во всех точках окружности |z| = 1; 3) если - 1 < Rе α ≤ 0, то Б. р. расходится в точке z = - 1 и условно сходится во всех остальных точках окружности |z| = 1. Во всех точках, в к-рых Б. р. сходится, он представляет главное значение функции (1 + z)α, равное 1 при z = 0. Б. р. является частным случаем гипергеометрического ряда.
Если z = x и α - действительные числа, причем α не есть целое неотрицательное число, то Б. р. ведет себя следующим образом: 1) если α > 0, то он абсолютно сходится при - 1 ≤ x ≤ 1 2) если α ≤ - 1, то Б. р. абсолютно сходится при - 1 < x < 1 и расходится при всех иных значениях х; 3) если - 1 < α ≤ 0, то Б. р. абсолютно сходится при - 1 < x < 1, условно сходится при х = 1 и расходится при х = - 1; при |х| > 1 Б. р. всегда расходится.
Б. р. появляется впервые, по-видимому, у И. Ньютона (I. Newton) в 1664-65. Исчерпывающее исследование Б. р. было проделано Н. Абелем [1]. Оно послужило началом теории степенных рядов в комплексной области.
Билет 25
25. Определение изображения по заданному оригиналу.
будем
рассматривать функции 
действительного
переменного 
,
заданные на 
.
Иногда будем считать, что 
определена
на 
,
но при 
функция 
.
Кроме того, будем предполагать, что
функция 
кусочно-непрерывна
и на каждом конечном промежутке имеет
конечное число точек разрыва первого
рода. Пусть 
-
комплексное число.
Рассмотрим функцию
.
(1)
Если
,
(2)
где 
,
то функция 
аналитическая
в полуплоскости 
(рис.
158).
Рис. 158
В самом деле,
,
(3)
так
как 
.
Законность дифференцирования по 
под
знаком интеграла следует из неравенства
(3) и того факта, что функция 
кусочно-непрерывна
(см. теорему 2 § 2.15).
Функция 
называется
изображением Лапласа функции 
, 
-изображением
или преобразованием Лапласа.
Мы будем употреблять обозначения
, 
, 
.
Функцию 
в
этом случае называют начальной функцией
или оригиналом. Число 
называется
показателем роста функции 
(ниже,
если особо не оговорено, то мы считаем,
что показатель роста 
равен 
).
Процесс нахождения изображения для заданного оригинала и обратно, нахождение оригинала по известному изображению называется операционным исчислением, начало которому положил Хевисайд. Разработав операционное исчисление, Хевисайд не дал ему обоснования. Отметим, что он рассматривал преобразование
,
т.е. 
.
В одних вопросах удобным является преобразование Лапласа, в других - преобразование Хевисайда. Мы будем рассматривать преобразование Лапласа.
Обоснование операционного исчисления было дано в двадцатых годах нашего века в работах ряда математиков.
Теорема
1 (единственности). Если две непрерывные
функции 
и 
имеют
одно и то же 
-изображение 
,
то они тождественно равны.
Мы не доказываем эту теорему.
На
основании теоремы 1 мы можем сказать,
что для непрерывной функции 
,
тождественно не равной нулю, изображение
не может быть периодической функцией.
В
самом деле, если 
,
где 
,
то
.
По теореме 1
,
т.
е. 
,
чего быть не может.