54. Вывод формулы Эйлера с помощью рядов Маклорена

ЭЙЛЕРА - МАКЛОРЕНА ФОРМУЛА

формула суммирования, связывающая частные суммы ряда с интегралом и производными его общего члена:

где  - Бернулли числа, R_n - остаточный член. С помощью Бернулли многочленов B_n(t), В _n(0)=В _п остаточный член записывается в виде:

Для n=2sостаточный член R_2s может быть представлен с использованием чисел Бернулли:

Если производные  и имеют одинаковые знаки и не меняют знака на [ р, т],то

Если, кроме того,

то Э.-М. ф. может быть записана в виде:

В такой форме Э. - М. ф. применяется, напр., при выводе Стирлинга формулы. В этом случае  и с - Эйлера постоянная. Имеются обобщения Э. - М. ф. на случай кратных сумм.  Э.-М. ф. применяется для приближенного вычисления определенных интегралов, для исследования сходимости рядов, для вычисления сумм и для разложения функций в рядТейлора. Напр., при т=1, р=0, п=2т+1,  Э.-М. ф. дает следующее выражение:

Э.-М. ф. играет важную роль при изучении асимптотич. разложений, в теоретико-числовых оценках, в конечных разностей исчислении.  Э.-М. ф. иногда применяется в виде:

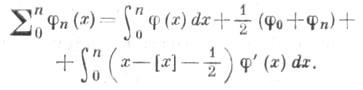
Э.-М. ф. была впервые приведена Л. Эйлером [1] в виде:    где S - сумма первых членов ряда с общим членом t(п), S=t=0 при n=0, а коэффициенты определяются рекуррентными соотношениями:

 

Билет 24

24. Определение изображения по заданному оригиналу.

 будем рассматривать функции  действительного переменного , заданные на . Иногда будем считать, что  определена на , но при  функция . Кроме того, будем предполагать, что функция  кусочно-непрерывна и на каждом конечном промежутке имеет конечное число точек разрыва первого рода. Пусть  - комплексное число.

Рассмотрим функцию

.            (1)

Если

,  (2)

где , то функция  аналитическая в полуплоскости  (рис. 158).

Рис. 158

В самом деле,

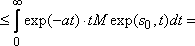
,           (3)

так как . Законность дифференцирования по  под знаком интеграла следует из неравенства (3) и того факта, что функция  кусочно-непрерывна (см. теорему 2 § 2.15).

Функция  называется изображением Лапласа функции , -изображением или преобразованием Лапласа.

Мы будем употреблять обозначения

, , .

Функцию  в этом случае называют начальной функцией или оригиналом. Число   называется показателем роста функции  (ниже, если особо не оговорено, то мы считаем, что показатель роста  равен ).

Процесс нахождения изображения для заданного оригинала и обратно, нахождение оригинала по известному изображению называется операционным исчислением, начало которому положил Хевисайд. Разработав операционное исчисление, Хевисайд не дал ему обоснования. Отметим, что он рассматривал преобразование

,

т.е. .

В одних вопросах удобным является преобразование Лапласа, в других - преобразование Хевисайда. Мы будем рассматривать преобразование Лапласа.

Обоснование операционного исчисления было дано в двадцатых годах нашего века в работах ряда математиков.

Теорема 1 (единственности). Если две непрерывные функции  и  имеют одно и то же -изображение , то они тождественно равны.

Мы не доказываем эту теорему.

На основании теоремы 1 мы можем сказать, что для непрерывной функции , тождественно не равной нулю, изображение не может быть периодической функцией.

В самом деле, если , где , то

.

По теореме 1

,

т. е.  , чего быть не может.