
- •17. Понятие фундаментальной системы решений линейных однородных диф уравнений.Вронскийан.
- •50.Ряды Тейлора и Маклорена. Вывод формулы для общего члена ряда Маклорена.
- •20. Лоду с пос коэф. Второго порядка
- •54. Вывод формулы Эйлера с помощью рядов Маклорена
- •24. Определение изображения по заданному оригиналу.
- •55.Биноминальный ряд
- •25. Определение изображения по заданному оригиналу.
- •56. Применение рядов для вычисления пределов
- •29. Преобразование Лапласа. Свойство подобия.
- •30 Преобразование лапласа. Интегрирование оригинала.
- •31 Преобразование Лапласа. Теорема запоздания.
Билет 17
17. Понятие фундаментальной системы решений линейных однородных диф уравнений.Вронскийан.
Фундаментальной системой решений однородного линейного дифференциального уравнения называется упорядоченный набор из n линейно независимых решений уравнения.
Иными словами любые n линейно независимых решений y1(x), y2(x),..., yn(x) уравнения y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = 0 образуют фундаментальную систему решений.
Доказано, что у однородного линейного дифференциального уравнения с непрерывными коэффициентами существует фундаментальная система решений.
Пусть задана некоторая линейно независимая система n векторов из Rn:
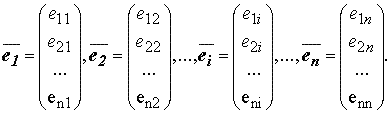
И пусть функции y1(x), y2(x),..., yn(x) — решения линейного однородного уравнения с начальными условиями:

Функции y1(x), y2(x),..., yn(x) образуют фундаментальную систему решений линейного однородного уравнения.
Вронскиа́н (определитель Вронского)
системы функций ![]() ,
дифференцируемых на промежутке
,
дифференцируемых на промежутке ![]() (n-1)-раз
— функция на
(n-1)-раз
— функция на ![]() ,
задаваемая определителем следующей матрицы:
,
задаваемая определителем следующей матрицы:
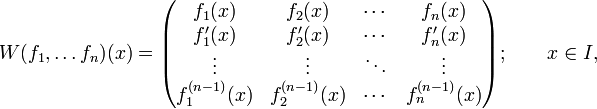 .
.
Также
вронскианом называют функцию, заданную
определителем более общего вида. А
именно, пусть задано n вектор-функций ![]() с
n компонентами:
с
n компонентами: ![]() .
Тогда определитель будет выглядеть так
(чтобы избежать разночтений обозначим
его
.
Тогда определитель будет выглядеть так
(чтобы избежать разночтений обозначим
его ![]() ):
):
 .
.
Определитель Вронского применяется для решения дифференциальных уравнений, например для того, чтобы узнать, являются ли найденные решения однородного линейного дифференциального уравнения (либо системы уравнений) линейно независимыми. Это помогает в поиске его общего решения.
48. представление функции ln(1+x) в виде степенного ряда.

Билет 18
18.Линейные однородные диф уравнения с пост коэффициентами второго порядка.
Случай различных диф корней характеристического уравнения.
Рассмотрим линейное дифференциальное уравнение вида
![]()
где p, q − постоянные коэффициенты. Для каждого такого дифференциального уравнения можно записать так называемое характеристическое уравнение:
![]()
Обшее решение однородного дифференциального уравнения зависит от корней характеристического уравнения, которое в данном случае будет являться квадратным уравнением. Возможны следующие случаи:
Дискриминант характеристического квадратного уравнения положителен: D > 0. Тогда корни характеристического уравнения k1 и k2 действительны и различны. В этом случае общее решение описывается функцией
![]()
где C1 и C2 − произвольные действительные числа.
Дискриминант характеристического квадратного уравнения равен нулю: D = 0. Тогда корни действительны и равны. В этом случае говорят, что существует один корень k1 второго порядка. Общее решение однородного дифференциального уравнения имеет вид:
![]()
Дискриминант характеристического квадратного уравнения отрицателен: D < 0. Такое уравнение имеет комплексно-сопряженные корни k1 = α + βi, k1 = α − βi. Общее решение записывается в виде
![]()
Рассмотренные три случая удобно представить в виде таблицы:
|
|
Если
все корни характеристического уравнения
(3) действительные и различные числа ![]() ,
то система решений
,
то система решений ![]() будет
линейно независимой, а общее решение
уравнения (2) запишется в виде:
будет
линейно независимой, а общее решение
уравнения (2) запишется в виде:
![]() , (4)
, (4)
где ![]() -
произвольные константы.
-
произвольные константы.
49. представление функции arctg x в виде степенного ряда.
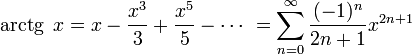
Билет 19
19. Лоду с пос коэф. Второго порядка.
Случай кратных действ корней характеристического уравнения
Случай различных диф корней характеристического уравнения.
Рассмотрим линейное дифференциальное уравнение вида
![]()
где p, q − постоянные коэффициенты. Для каждого такого дифференциального уравнения можно записать так называемое характеристическое уравнение:
![]()
Обшее решение однородного дифференциального уравнения зависит от корней характеристического уравнения, которое в данном случае будет являться квадратным уравнением. Возможны следующие случаи:
Дискриминант характеристического квадратного уравнения положителен: D > 0. Тогда корни характеристического уравнения k1 и k2 действительны и различны. В этом случае общее решение описывается функцией
![]()
где C1 и C2 − произвольные действительные числа.
Дискриминант характеристического квадратного уравнения равен нулю: D = 0. Тогда корни действительны и равны. В этом случае говорят, что существует один корень k1 второго порядка. Общее решение однородного дифференциального уравнения имеет вид:
![]()
Дискриминант характеристического квадратного уравнения отрицателен: D < 0. Такое уравнение имеет комплексно-сопряженные корни k1 = α + βi, k1 = α − βi. Общее решение записывается в виде
![]()


