§ 8. Эксцентриситет гиперболы

Определение: Эксцентриситетом ε гиперболы называется отноше-ние её фокусного расстояния к расстоянию между её вершинами.

Если действительной осью гиперболы является ось ОХ, то её эксцентриситет выражается формулой

ε =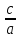 (32).

Т. к. для гиперболы с а, то

ε 1 (33).

Приняв во внимание соотношение (26), получим

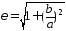(34),

(35).

§ 9. Фокальные радиусы гиперболы

Определение: Фокальными радиусами точки М гиперболы называются отрезки, соединяющие эту точку с фокусами F₁ и F₂ гиперболы.

Их длины выражаются формулами (36) и (37) для правой ветви гиперболы

r₁ = F₁M = +a = ε + a (36),

r₂ = F₂M = –a = ε – a (37).

и формулами (38) и (39) – для левой ветви

r₁ = F₁M = – 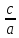– a = – ε – a (38),

r₂ = F₂M = – +a = – ε + a (39).

§ 10. Равносторонняя гипербола как график обратной

пропорциональной зависимости

В школьной программе гипербола определяется уравнением

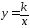(40).

Это уравнение выражает обратную пропорциональную зависи-мость переменных величин х и у. В выражении (40) нелегко распо-знать (увидеть) связь с каноническим уравнением (25) гиперболы.

При 0 график гиперболы имеет вид

у = х

у = - х

Рис. 5

Для параболы (38) центр координатной системы является центром симметрии. А прямые у = х и у = – х являются осями симметрии.

Совершим поворот осей ОХ и ОУ на 45⁰ против часовой стрелки. В матричной форме этот переход будет иметь вид

= (41)

или

(42).

Представим уравнение (38) в виде

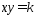(43).

Подставим в левую часть этого уравнения выражения для х и у из системы (40)

[()² – ()²] = или ()² – ()² = 2

Тогда

Т. е. получаем уравнение той же гиперболы (но повёрнутой на 45⁰ против часовой стрелки) в каноническом виде (Рис. 6).

Рис. 6

§ 11. Директрисы эллипса и гиперболы

Определение: Директрисами эллипса называются две прямые,

перпендикулярные к большой оси эллипса и расположенные

симметрично относительно центра на расстоянии от него.

Если эллипс задан каноническим уравнением (8), причём ab, то в выбранной системе координат его директрисы определяются уравнениями и(44).

Рис. 8

Т. к. для эллипса 0 ε 1, тоa. Это означает, что директрисы эллипса не имеют с ним общих точек.

Определение: Директрисами гиперболы называются две прямые, перпендикулярные к большой оси гиперболы и расположенные симметрично относительно центра на расстоянии

от него.

Если гипербола задана каноническим уравнением (25), то в данной системе координат её директрисы определяются уравнениями (44).

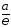
Поскольку для гиперболы ε 1, тоa. Это означает, что директрисы гиперболы не имеют с ней общих точек.

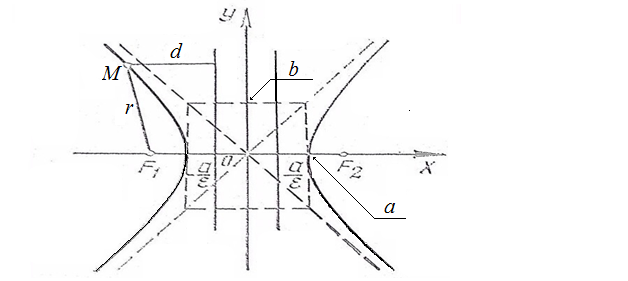
Рис. 9

Важное свойство директрис эллипса и гиперболы выражает следующая теорема.

Теорема. Отношение расстояния r произвольной точки эллипса (гиперболы) до фокуса к расстоянию d этой точки до соответствующей директрисы есть постоянная величина, равная

Доказательство. Рассмотрим, например, левый фокус и левую директрису эллипса. Пусть ()М(х;у) – произвольная точка эллипса (рис. 8). Здесь

r = a + εx, d = – (– 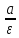) =x + .

Если ()М(х;у) – произвольная точка левой ветви гиперболы

(Рис. 9), то

r = – εx – a, d = – x – .

.

Свойство, выраженное вышеприведённой теоремой, может быть положено в основу определения эллипса и гиперболы.

Множество всех точек плоскости, для которых отношение расстояния r до фиксированной точки (фокуса) к расстоянию d до фиксированной прямой (директрисы) есть – величина постоянная. Причём фигура оказывается эллипсом при 1 и – гиперболой при 1.

Вопрос о том, что представляет собой это множество точек в случае 1, рассматривается в следующем параграфе.