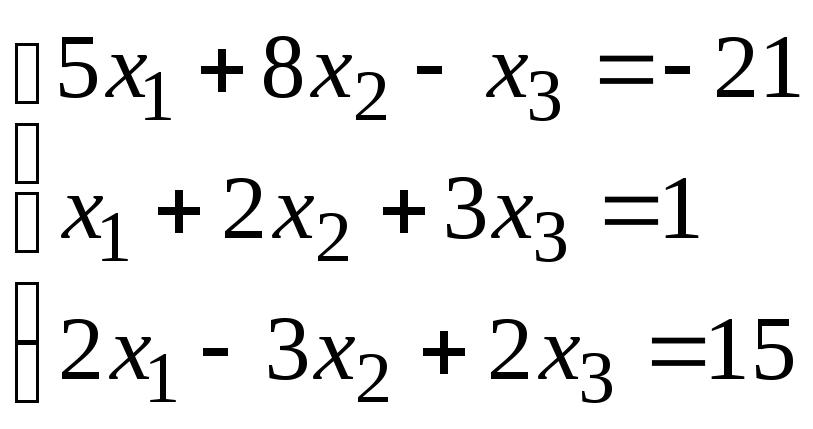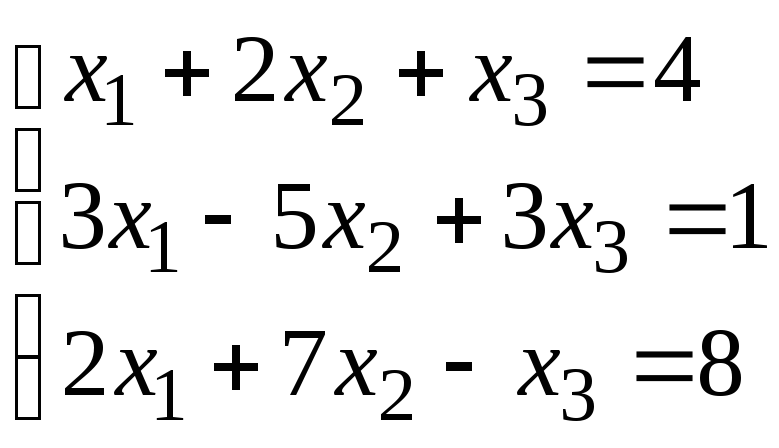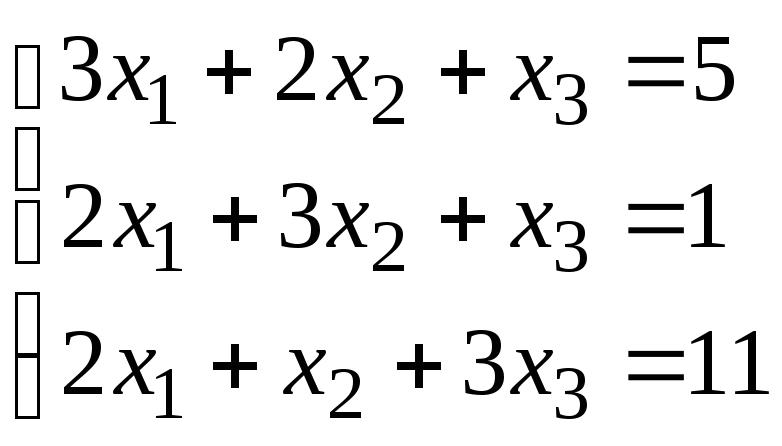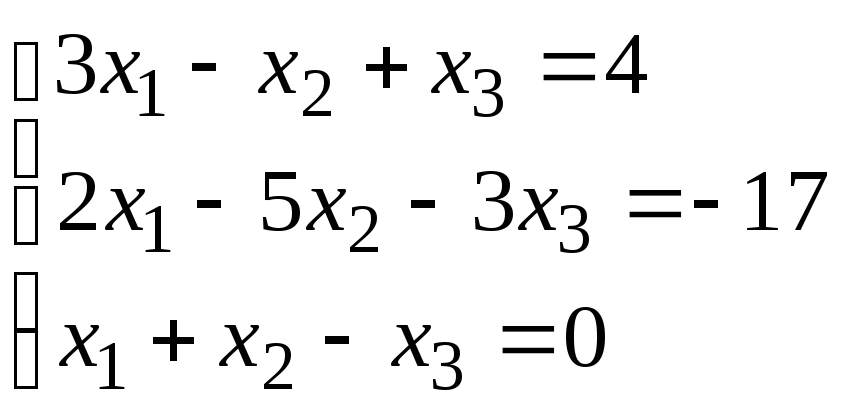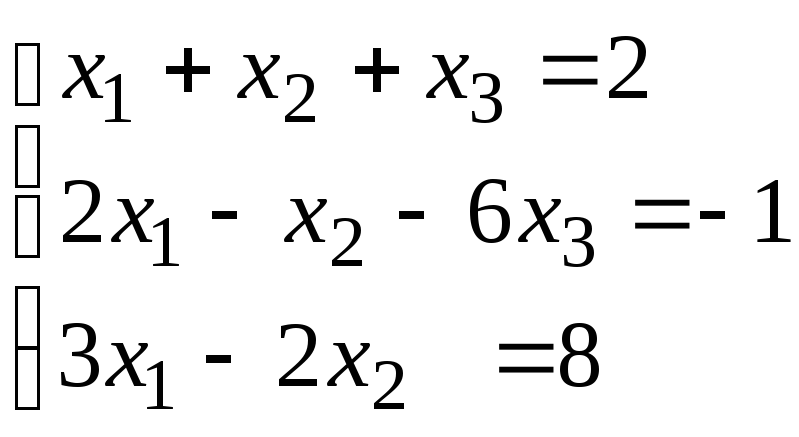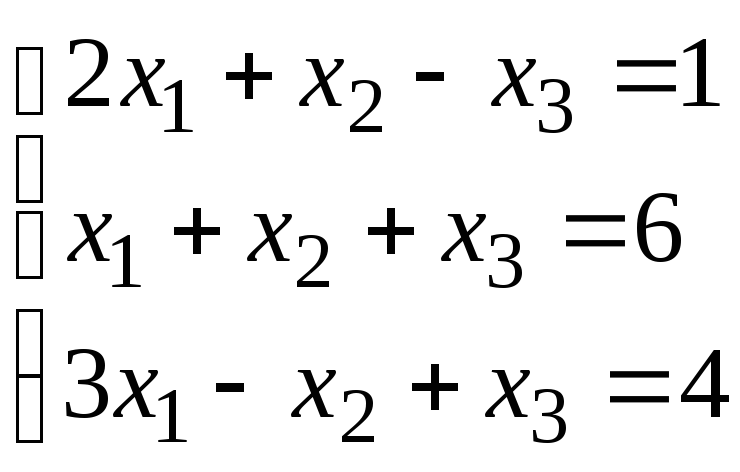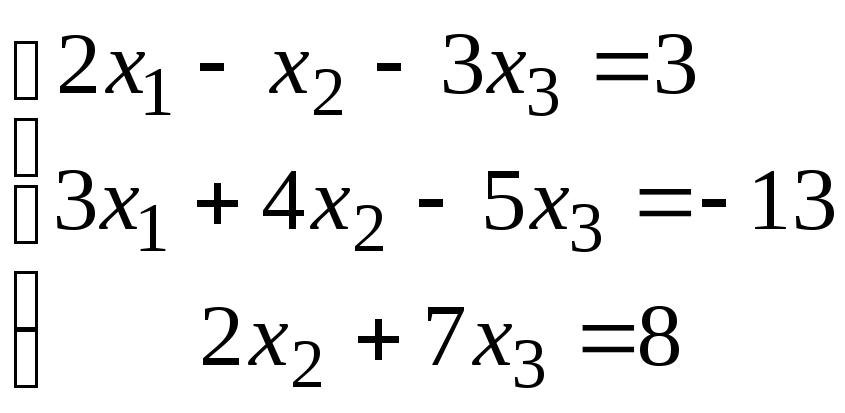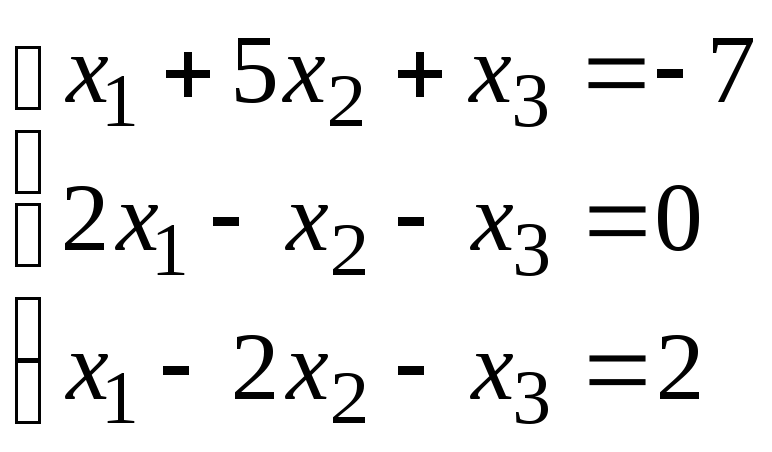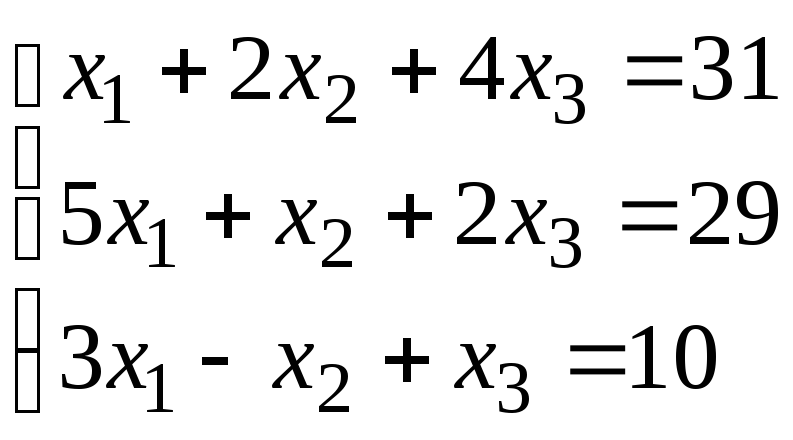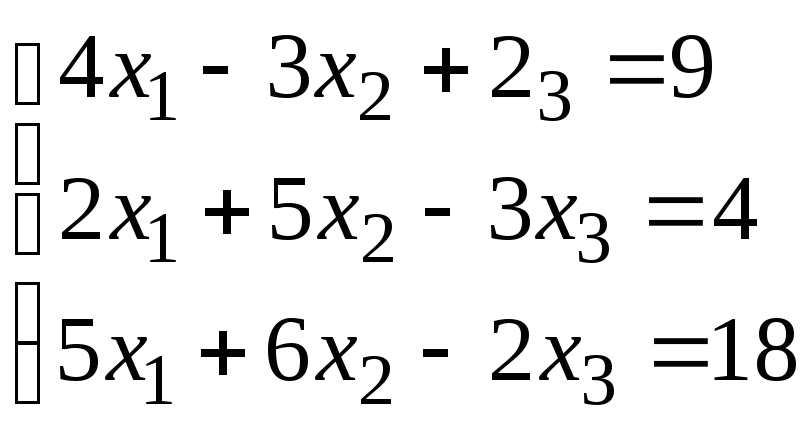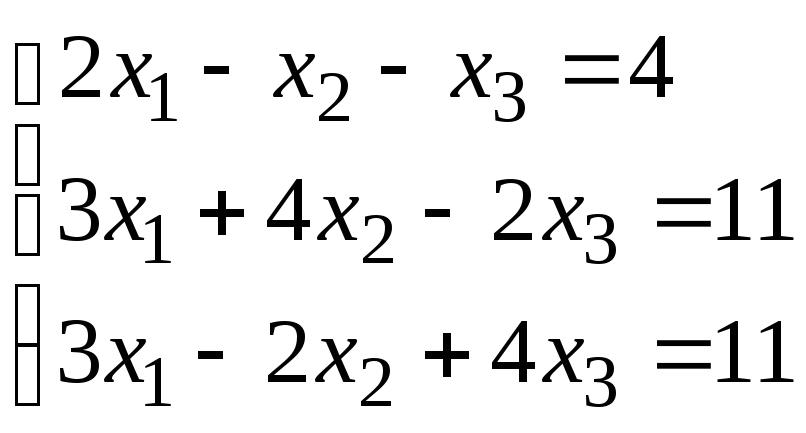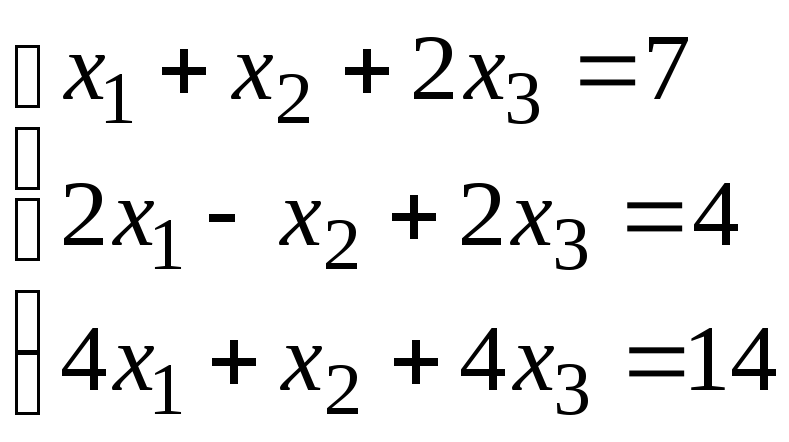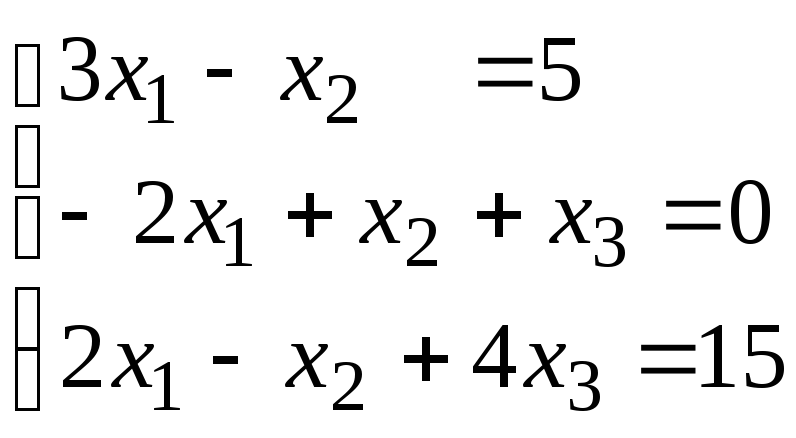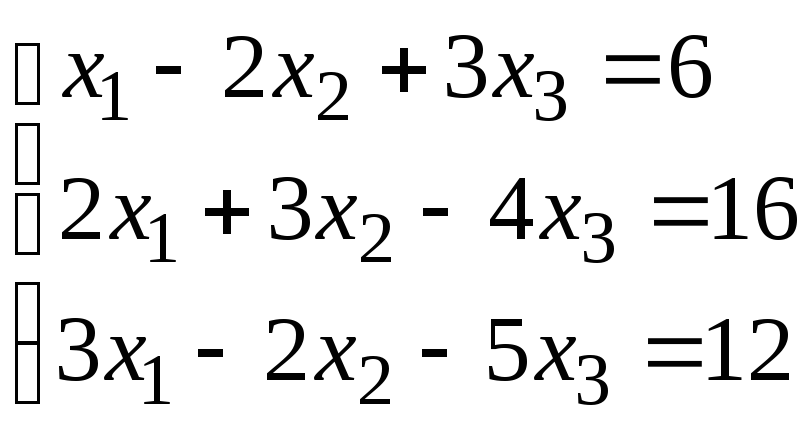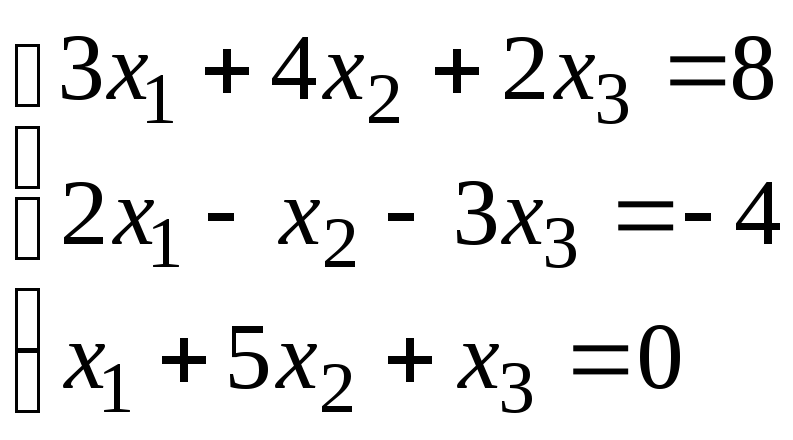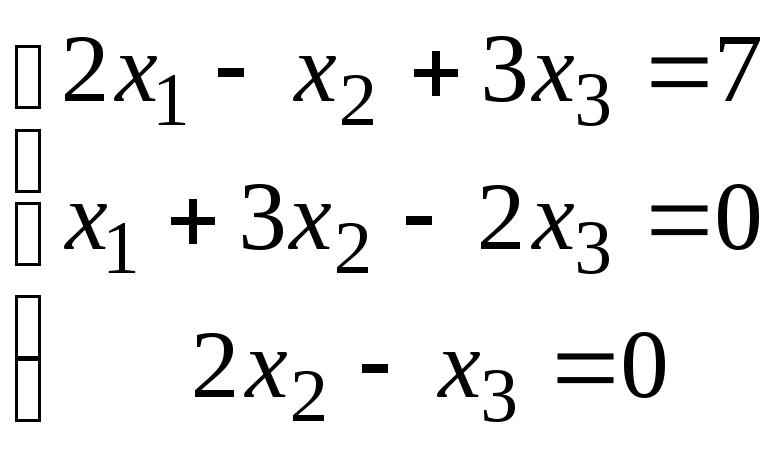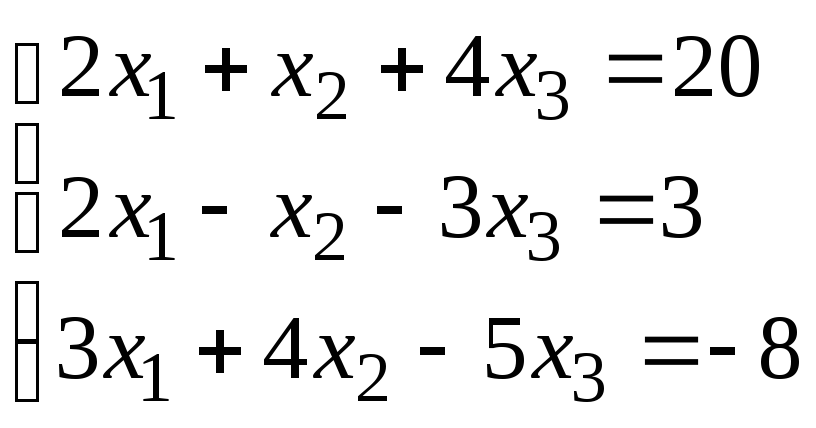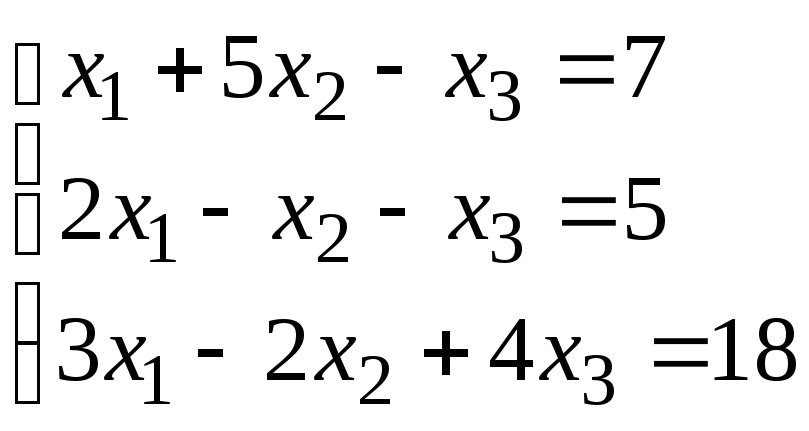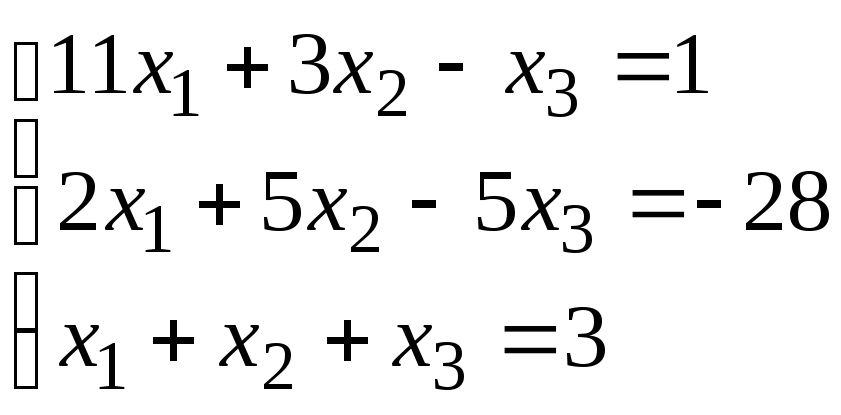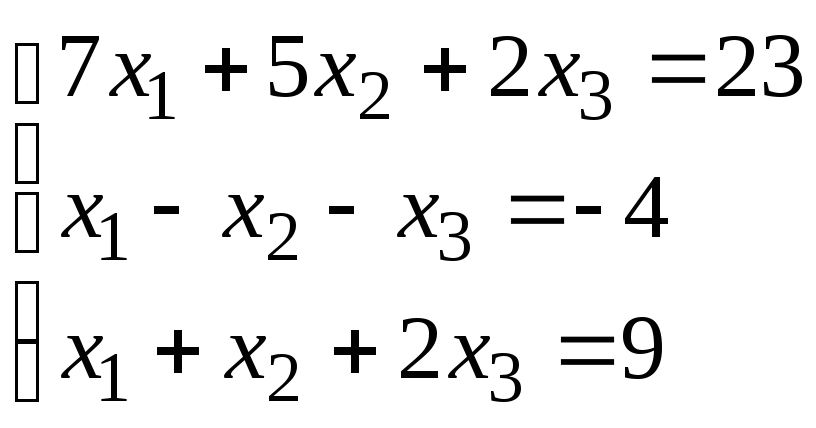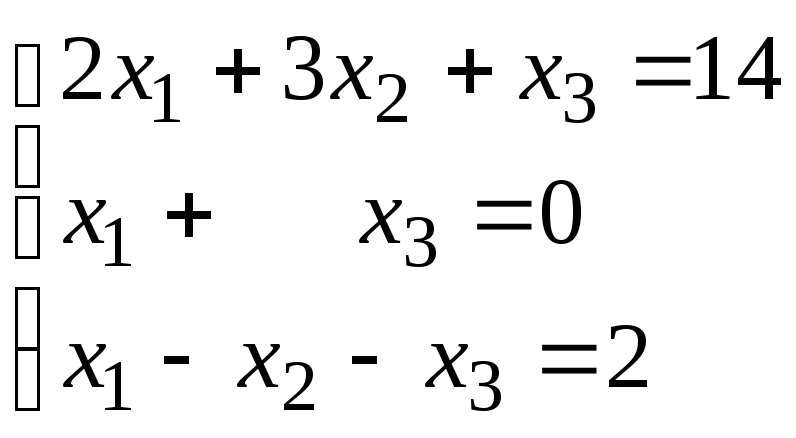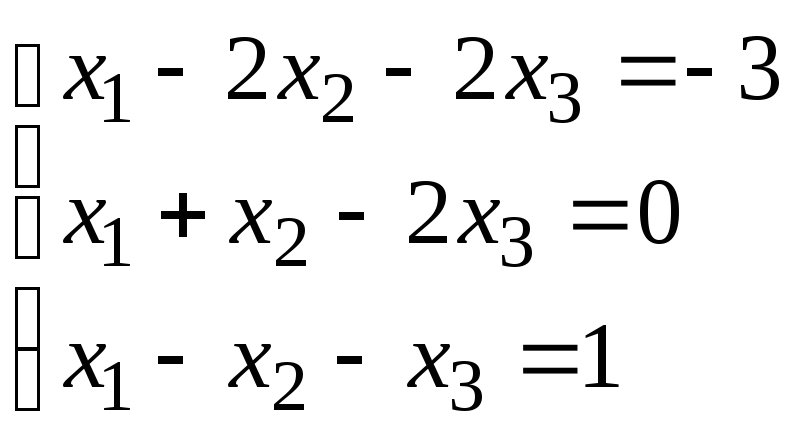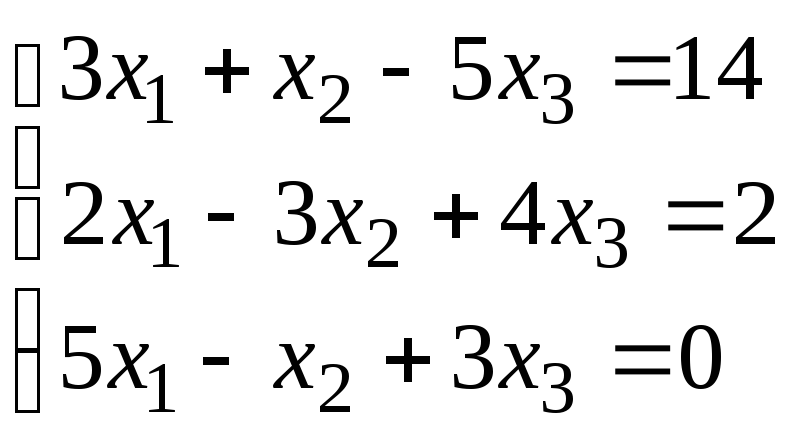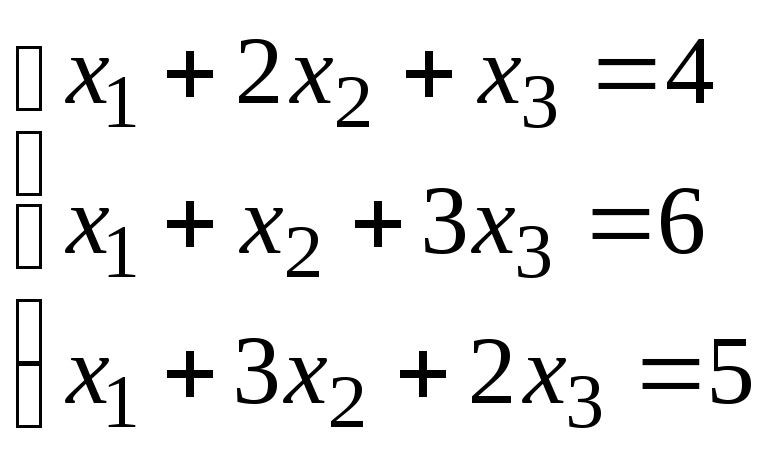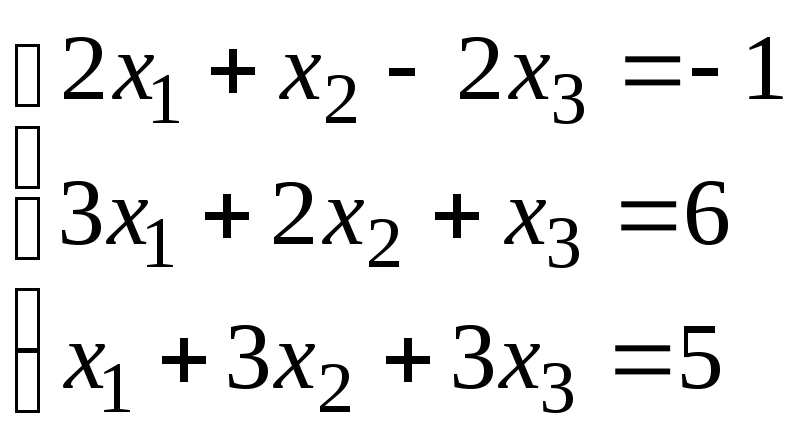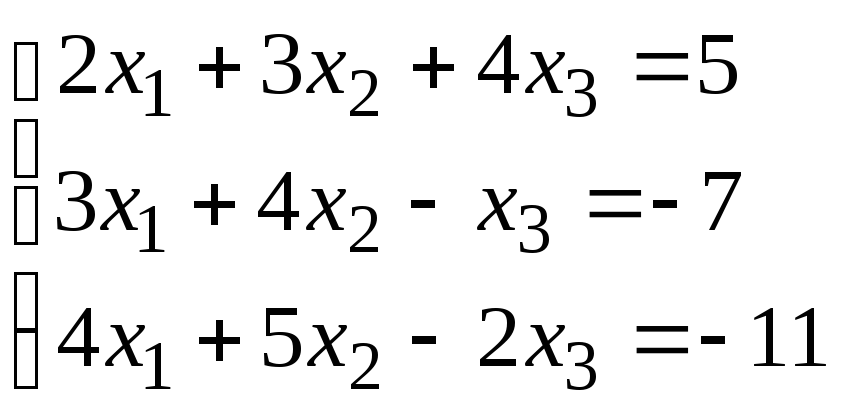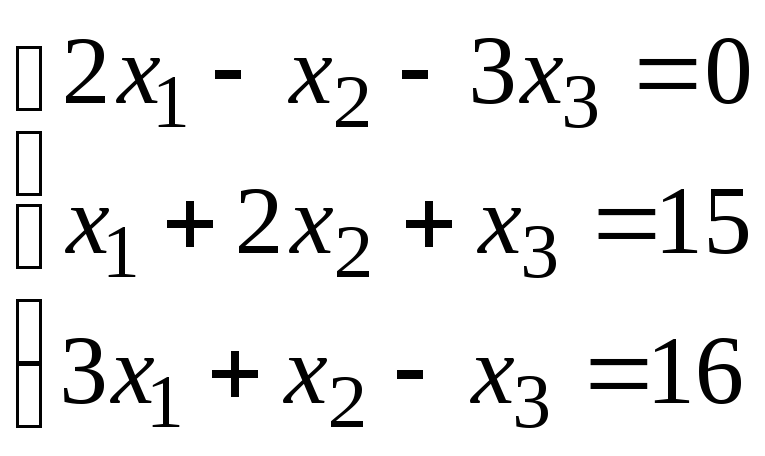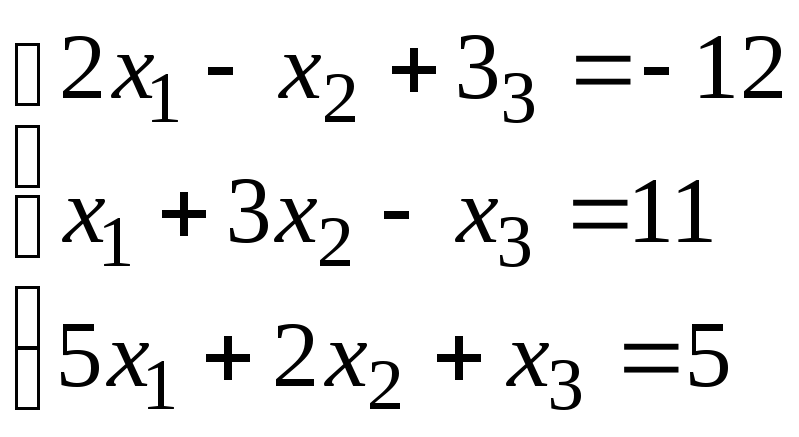- •Математика
- •Санкт-Петербург
- • СПб гу га, 2010 Расчетно-графическая работа на тему: «Решение систем линейных уравнений»
- •Варианты индивидуальных заданий.
- •Расчетно-графическая работа на тему: «Применение векторной алгебры к задачам аналитической геометрии». Задание.Даны координаты точекA,b,c,DиE.
- •Расчетно-графическая работа на тему: «Исследование функции одной переменной»
- •Варианты индивидуальных заданий.
- •Расчетно-графическая работа по теме «Функции двух независимых переменных»
- •Для выполнения задания 1 необходимо
- •Для выполнения задания 2 необходимо
- •Расчетно-графическая работа по теме « Определенный интеграл»
Министерство транспорта Российской Федерации (Минтранс России)
Федеральное агентство воздушного транспорта (Росавиация)
ФГОУ ВПО « Санкт-Петербургский государственный
университет гражданской авиации »
Математика
Методические указания для выполнения расчетно-графических работ
Санкт-Петербург
2010
Одобрено и рекомендовано к изданию Учебно–методическим советом Университета
МАТЕМАТИКА: Методические указания для выполнения расчетно-графических работ / Университет ГА». С.-Петербург, 2010.
Методические указания разработаны для индивидуального выполнения расчетно-графических работ, предусмотренных программой курса математики.
Предназначены для студентов 1-го и 2-го семестров обучения КФ, ФЛЭ, ФААП, ИТФ, ГФ.
Составители: Л. И. Загорская, доцент,
О. И. Нездерова, доцент,
Ю.Е. Кольчинская, ст. преподаватель.
Рецензент: В. И. Арбузов, д-р физ.-мат. наук, проф.
СПб гу га, 2010 Расчетно-графическая работа на тему: «Решение систем линейных уравнений»
Задание 1. Дана система линейных уравнений.
Решить систему тремя способами:
методом Крамера,
матричным методом,
методом Гаусса.
Сделать проверку.
Для выполнения задания 1 необходимо выбрать из таблицы №1 индивидуальный вариант, номер которого совпадает с порядковым номером по журналу.
Задание 2.
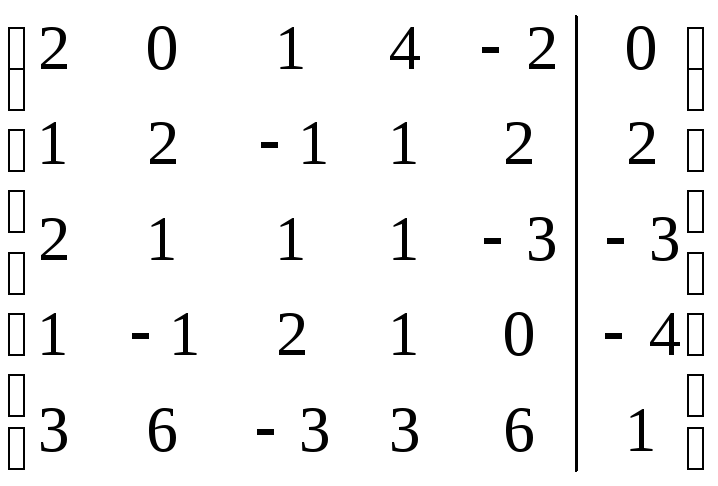
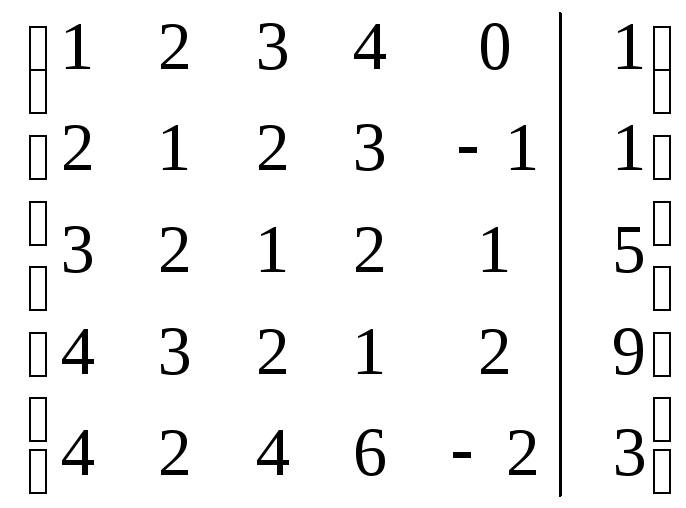
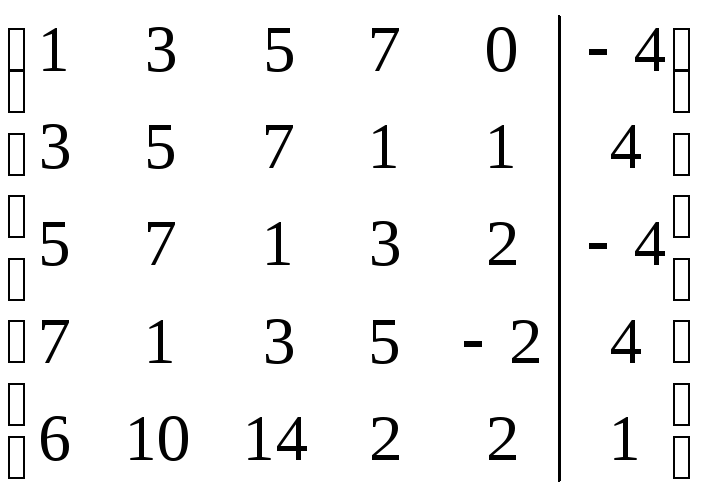
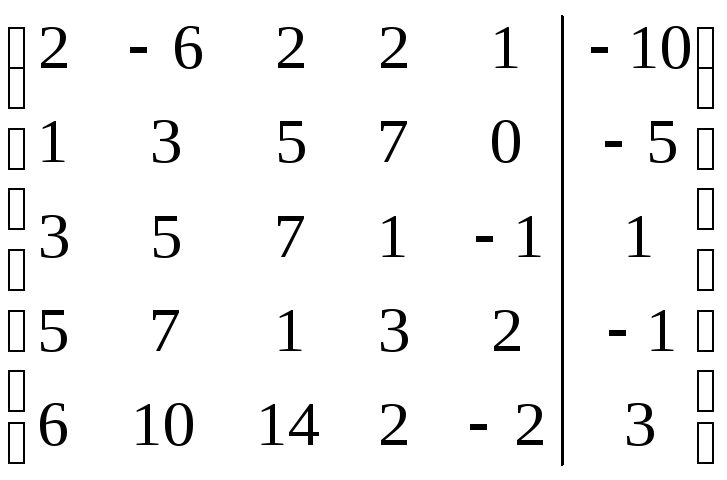
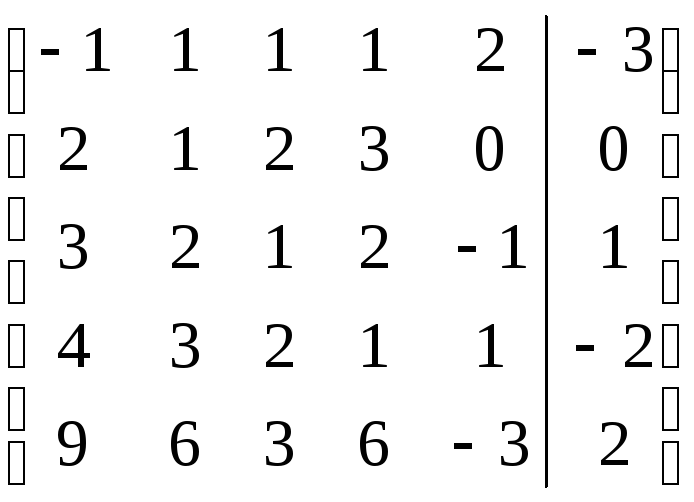
Дана
расширенная матрица системы линейных
уравнений
![]() ,
где
,
где![]() ,
,![]() .
.
Записать
три системы линейных уравнений,
используя матрицы
![]() и
и![]() указанной размерности.
указанной размерности.
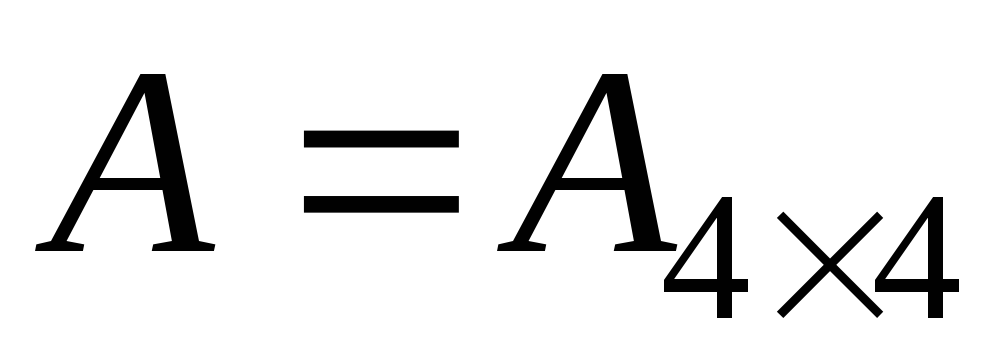 (выбрать
первые четыре строки и четыре первых
столбца матрицы
(выбрать
первые четыре строки и четыре первых
столбца матрицы
 ),
),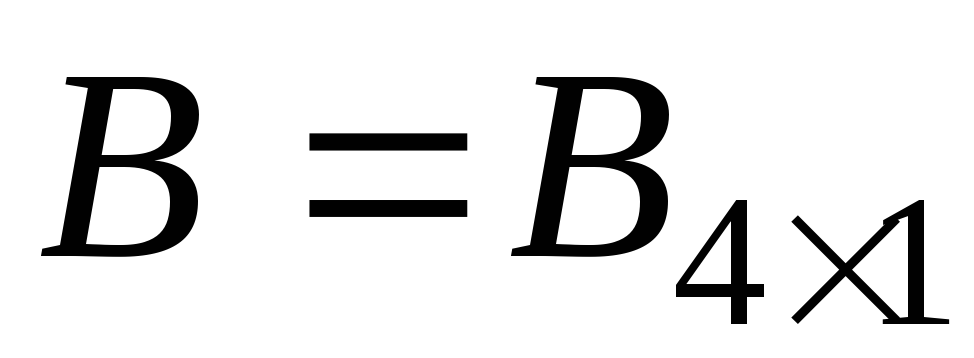 (выбрать четыре первых строки матрицы
(выбрать четыре первых строки матрицы );
);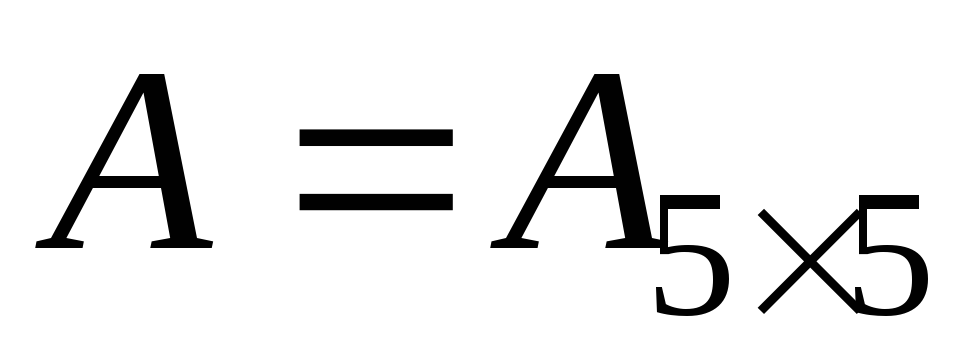 ,
,
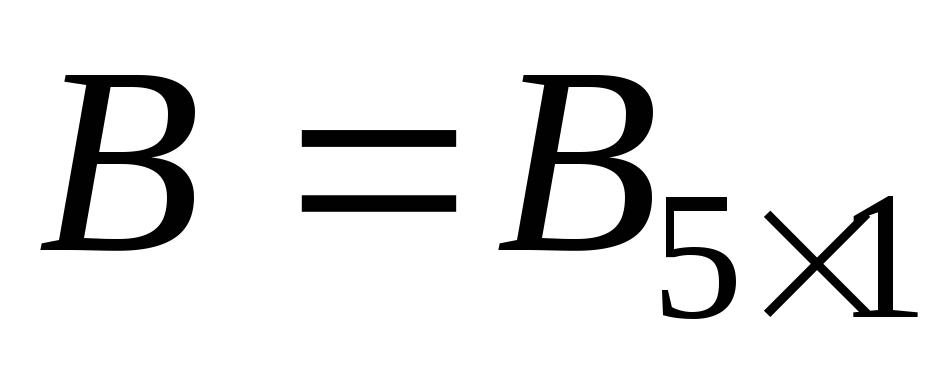 ;
;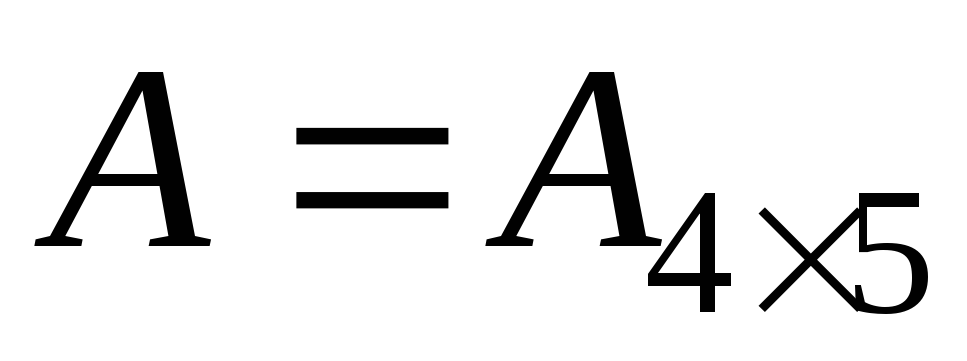 (выбрать
первые четыре строки и пять столбцов
матрицы
(выбрать
первые четыре строки и пять столбцов
матрицы
 ),
),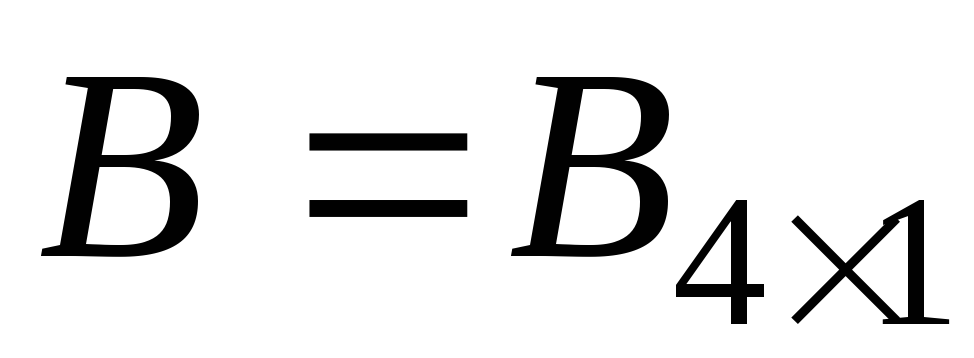 (выбрать четыре первых строки матрицы
(выбрать четыре первых строки матрицы ).
).
Исследовать каждую из полученных систем на совместность. Если система совместна, решить ее методом Гаусса.
Для выполнения задания 2 необходимо выбрать из таблицы №2 индивидуальный вариант, номер которого совпадает с порядковым номером по журналу.
Варианты индивидуальных заданий.
Таблица № 1.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица № 1 (продолжение).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица № 2.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица № 2 (продолжение).
|
|
|
|
13.
|
14.
|
|
15.
|
16.
|
|
|
|
|
|
|
Таблица № 2 (продолжение).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|