Матан / Шпаргалка по векторной алгебре и аналит. геометрии

Векторная алгебра.

, где , , .

, . Тогда .

Орт вектора вектор единичной длины, совпадающий с по направлению, .

Скалярное произведение векторов и .

Обозначение: или .

Определение: , где угол между векторами.

Формула для вычисления в ортонормированном базисе: .

,

Векторное произведение векторов и .

Обозначение: или .

Определение: есть вектор:

1) () и ();

2) , где угол между векторами;

3) образуют правую тройку, и ()().

Формула для вычисления в ортонормированном базисе: .

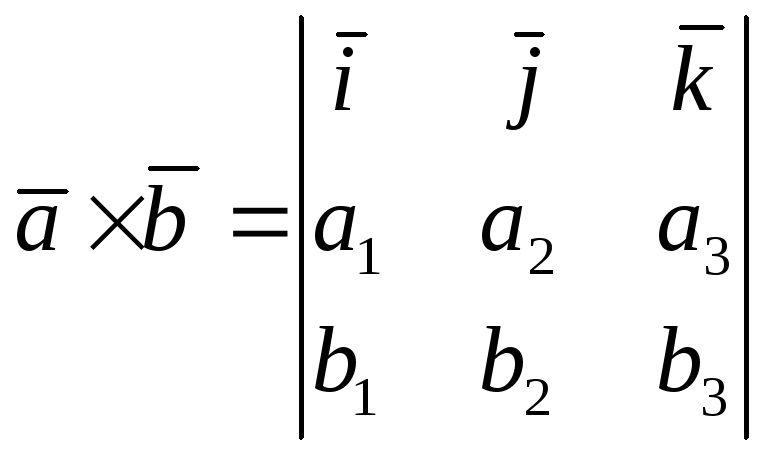Геометрический смысл: , где площадь параллелограмма, построенного на

перемножаемых векторах, и, соответственно, .

Физическая интерпретация: , где

сила, приложенная в , момент силы относительно ,

и, следовательно, моменты силы относительно осей , , .

Смешанное произведение векторов , , .

Обозначение: (без каких-либо промежуточных знаков).

Определение: .

Формула для вычисления в ортонормированном базисе: .

Геометрический смысл: , где объём параллелепипеда, построенного на

перемножаемых векторах, и, соответственно, .

Условия коллинеарности, ортогональности и компланарности векторов.

компланарны (т.е. лежат в одной плоскости)

Аналитическая геометрия.

Общий вид уравнения поверхности в пространстве: .

Общий вид уравнения линии в пространстве: или .

Общий вид уравнения линии на плоскости: или .

Если в уравнении геометрического объекта отсутствует координата (или , или ),

то объект параллелен оси (или , или ).

Прямая на плоскости.

Общий вид уравнения: , вектор прямой.

{уравнение оси } ; {уравнение оси } .

Прямая, проходящая через точку перпендикулярно вектору :

.

Прямая, проходящая через точку параллельно вектору :

.

нормаль прямой, направляющий вектор.

Прямые и

перпендикулярны, если , т.е. ;

параллельны, если , т.е. ;

совпадают, если .

Координаты точки пересечения прямых и решение системы уравнений

.

Угол между прямыми угол между их нормалями или их направляющими векторами.

или .

Плоскость в пространстве.

Общий вид уравнения: , вектор плоскости.

{уравнение плоскости } ; {} ; {} .

Уравнение плоскости через точку перпендикулярно вектору :

.

Плоскости

и

перпендикулярны, если , т.е. ;

параллельны, если , т.е. ;

совпадают, если .

Угол между плоскостями и угол между их нормалями.

Прямая в пространстве.

Общий вид уравнения: .

Вектор, параллельный прямой, т.е. направляющий вектор .

Уравнения координатных осей:

{ось } ; {ось } ; {ось } .

Прямая, проходящая через точку параллельно вектору :

(каноническое уравнение прямой)

или (параметрическое уравнение прямой).

Прямые и

перпендикулярны, если , т.е. ;

коллинеарны, если , т.е. ;

скрещиваются, если вектора и

не являются компланарными.

Угол между прямыми угол между их направляющими векторами и .

Прямая и плоскость в пространстве.

Плоскость : с нормальным вектором

и прямая : с направляющим вектором

перпендикулярны, если ;

параллельны, если и .

Прямая лежит в плоскости , если и .

Если угол между прямой и плоскостью , то есть угол между и ,

и, следовательно, .

Координаты точки встречи прямой и плоскости решение системы уравнений

.

Если система не имеет решений, прямая параллельна плоскости.

Если решений бесконечно много, прямая лежит в плоскости.

Кривые второго порядка.

Канонические уравнения:

эллипс;

, гипербола;

, парабола.

Вырожденные варианты:

точка; мнимый эллипс (пустое множество);

пара прямых ; .

Любое уравнение вида

заменой положения координатных осей на плоскости (т.е. соответствующей заменой переменных) приводится к одному из канонических, представленных выше.

Если собственные числа матрицы , то

при будет получено уравнение эллипса,

при уравнение гиперболы,

при уравнение параболы.

Алгоритм приведения уравнения

(1)

к каноническому виду.

Этап 1 (проводится только при , т.е. при наличии слагаемого, содержащего произведение переменных).

Производится поворот осей координат, новые оси коллинеарны собственным векторам и матрицы . Вектора должны быть нормированы, тогда при замене уравнение (1) принимает вид

(2).

Этап 2.

Используя формулу выделения полного квадрата , получаем один из вариантов:

(при ),

или (при )

Переносим начало координат в точку не меняя направления осей. Во вновь полученной системе координат , где , уравнение (1) преобразуется в одно из канонических. Следует помнить, что при будет получено уравнение эллипса, при уравнение гиперболы, при урав-нение параболы.